基于R语言的机器学习多分类任务（决策树、随机森林、朴素贝叶斯、支持向量机、KNN、BP神经网络）——UCL胎心宫缩监护数据（CTG.xls）预测分析

2023-11-08 11:20
文章标签 语言 学习 分类 机器 监护 神经网络 决策树 预测 bp 贝叶斯 朴素 knn 随机 森林 向量 xls ctg ucl 宫缩 胎心

本文主要是介绍基于R语言的机器学习多分类任务（决策树、随机森林、朴素贝叶斯、支持向量机、KNN、BP神经网络）——UCL胎心宫缩监护数据（CTG.xls）预测分析，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

摘要：本文针对UCL胎心宫缩监数据（Y有三个水平的多分类预测任务），利用R语言建立决策树、随机森林、朴素贝叶斯、支持向量机、KNN和BP神经网络模型进行预测。给出了任务（包括数据预处理（缺失值处理、异常值处理）、建模、模型评价等步骤）的详细代码，读者稍加改动便可运用到自己的机器学习分类任务中。

一、数据来源与说明

胎心宫缩监护（CTG.xls）来源于UCI机器学习数据库。数据有2129个观测值及23个变量，包含了致命心律的各种度量以及基于监护记录的由专家分类的公所特征。数据可以从http://archive.ics.uci.edu/ml/machine-learning-databases/00193/获得。

  • 任务：尝试用前面的22个变量作为自变量预测作为因变量的NSP类别。

变量描述如下：
变量描述
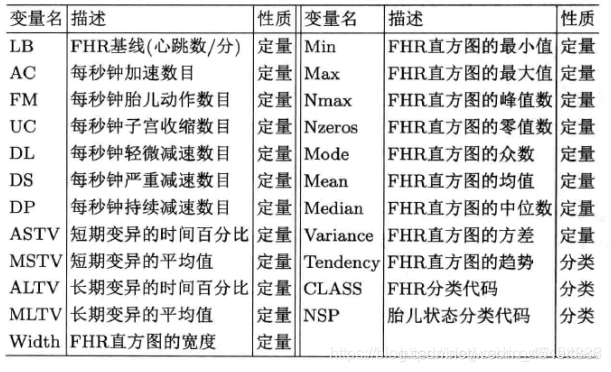
最后三个分类变量的水平为：
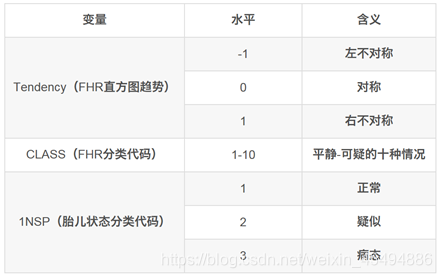
分类变量水平

二、实验准备

在这里插入图片描述
打开数据表发现数据非常杂乱，表头第一行不是变量名，因此需要进行必要的数据处理，使得读进来的数据满足可分析、建模的整洁格式。处理代码如下。

#======================实验准备 =========================#下载程序包if(!require(tidyverse)) install.packages("tidyverse")  
if(!require(readxl)) install.packages("readxl")
if(!require(VIM)) install.packages("VIM")
if(!require(randomForest)) install.packages("randomForest")  
if(!require(magrittr )) install.packages("magrittr ")       
if(!require(caret)) install.packages("caret")  
if(!require(e1071)) install.packages("e1071")   
if(!require(pROC)) install.packages("pROC")   
if(!require(PerformanceAnalytics)) install.packages("PerformanceAnalytics")   
if(!require(DT)) install.packages("DT")    
if(!require(partykit)) install.packages("partykit")   
if(!require(class)) install.packages("class")  
if(!require(neuralnet)) install.packages("neuralnet")#==========================导入数据 ======================#设置工作路径
getwd()
setwd("c:/ctg")#读取数据
data <-
read_excel("CTG.xls",sheet=2) #下载数据为excel文件#获取指定数据集的列名
col_num <- c(1:23) %>%
as.character() #读进以后所需数据的列名为数字1:23(cols <- data[1,col_num]
%>% as.matrix() %>% as.vector()) #获取数字对应的真正的变量名names(data) <- data[1,]
%>% as.matrix() %>% as_vector() #重命名数据框data <- data[-1,cols] #获取最终所需数据(2129*23)glimpse(data) #查看数据

三、数据预处理

#========================数据预处理 ==================
#转变数据类型data <- data %>%  #先全部变数值型,再将三个分类变量因子化mutate_if(.predicate = is.character,.funs =
as.numeric) %>% mutate_at(.vars =
vars(Tendency,CLASS,NSP),.funs = as.factor) %>% glimpse()#数据写出
#write_csv(data,'data.csv')#summary汇总
summary(data)#缺失值分析
dev.new()   #新窗口用来保存图片
aggr(data, prop = F, numbers
= T)    # 可视化缺失值情况
which(complete.cases(data)==F)      ##缺失值的行号,一共三个缺失值
matrixplot(data)##删除含有缺失值的样本（2126）和数据去重，最后剩余2,114 x 23
data <- na.omit(data)
%>% unique() 
dim(data)#再次进行缺失数据识别
is.na(data)  
sum(is.na(data))#异常值的识别
boxplot(data,horizontal =
TRUE)  #异常值处理
#箱线图法
outliers <-
function(x,scale=1.5,lower=T,upper=T){q1 <- quantile(x,0.25)q3 <- quantile(x,0.75)iqr <- q3 - q1lower_bound <-  q1 - (scale * iqr)upper_bound <-  q3 + (scale * iqr)#识别异常值if(lower){   x[x<=lower_bound] <- lower_bound}if(upper){x[x>upper_bound] <- upper_bound}return(x)
}#对FM试验做异常值处理
FM <-  outliers(data$FM)#盖帽法
block<-function(x,lower=T,upper=T){if(lower){q1<-quantile(x,0.1)x[x<=q1]<-q1}if(upper){q95<-quantile(x,0.95)x[x>q95]<-q95}return(x)
}FM1 <-  block(data$FM)#绘图比较
dev.new()
par(mfrow = c(1, 2))  
boxplot(FM,xlab='箱线图法')
boxplot(FM1,xlab='盖帽法')#选择四分位数法对数值型变量进行异常值处处理
data_num  <- sapply(data[,1:20],outliers)
data_num %>% is.null()
%>% sum() #查看有无处理失败导致的空值#查看数值型变量间的相关性
dev.new()
chart.Correlation(data_num,histogram
= T)
chart.Correlation(data[1:20],histogram
= T)#合并数值型变量和分类变量
data_fill <-
cbind(data_num,data[,21:23])
dim(data_fill)dev.new()
boxplot(data_num,frame = T)

结果解读：

  • 缺失值分析

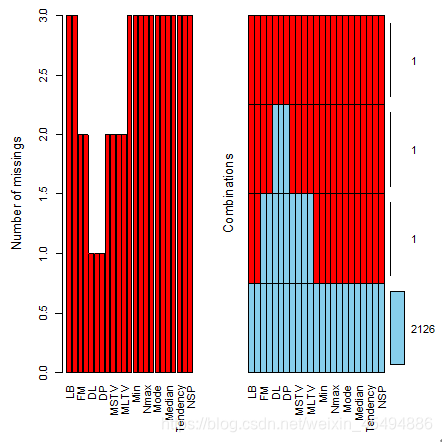
在这里插入图片描述

应用R语言VIM包中的aggr及matrixplot函数对缺失值进行可视化分析，左图为缺失值数量的柱状图，右图及下图反应缺失值的基本分布情况。通过缺失值可视化可以看数据集质量较好，仅有3个实例缺失值较多，基于时间成本和处理成本综合考量，将缺失实例直接做删除处理。

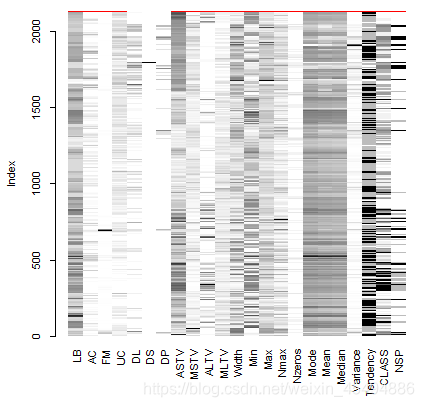
在这里插入图片描述
上图直观展示每个实例数据的分布情况，并用灰度来表示数值大小：浅色标志数值小，深色标志数值大，默认用红色标记缺失值。

  • 异常值处理
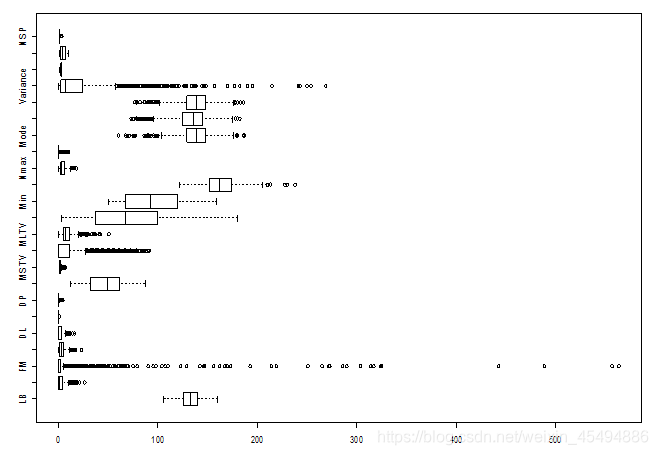
    在这里插入图片描述

从箱线图可以看出，FM、Variance等部分变量的异常值较多。

但是，且慢。数据分析建模的前提是对“业务”的充分理解。我们不能简单的把箱线图轴须以外的值就认为是异常值，而是应该结合挖掘目标和业务背景等综合判定。但这份数据集的元数据中给出的变量说明信息很少，并未说明记录时间的单位等信息，给异常数据判断增加了难度。经查“胎动不应该以分钟来计算，胎动在一个小时内的表现并没有规律性，所以一分钟无法得到准确的结果，正常情况下胎动是按小时计算。而且开始计算胎动的时间段也有所要求，在孕前中期根本没有这种说法，在孕后期二十八周以后，胎动增加才需要适当的计数。一般孩子的胎动一小时在三次差不多。”综合老师给出的变量说明，判断胎动数据的记录确实出现了异常值。

受信息所限，结合特征含义分析后，暂且简单地认为变量在箱线图轴须以外的观测值均为正常测量，经异常值处理后再用于建模分析。

以变量FM为例，利用传统的箱线图四分位距异常值处理法（认为（q1-1.5IQR,q3+1.5IQR）以外数据为异常值）和盖帽法（这里定义0.1和0.9分位数以外的数值为异常值法两种方法对FM变量进行异常值处理并做对比，将结果绘图如下。
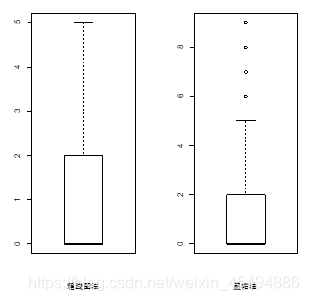
在这里插入图片描述
盖帽法保留了轴须外的部分数据，异常的分位范围也可选，其实这些轴须外数据也可能蕴含重要信息，但是这里，我们为了统一处理，采用四分位距法对所有数值型变量做异常值抹平，处理后结果如下。
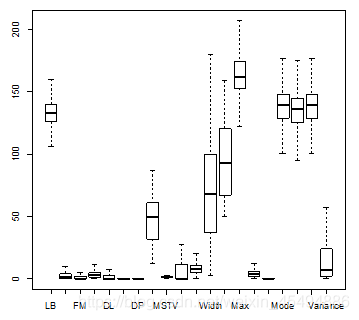
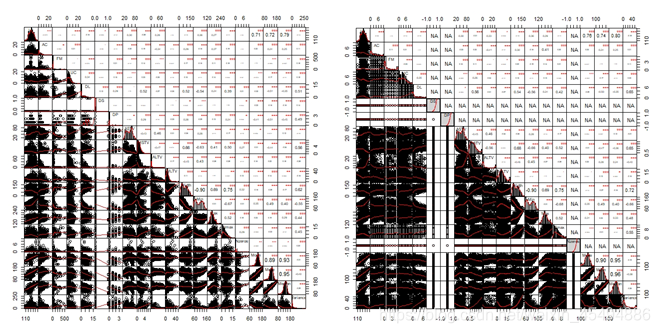
在这里插入图片描述在这里插入图片描述
左图是异常值处理前的变量关系图，右图是异常值处理后 变量间关系图。从图上看来，异常值管理后，数据明显变得更加紧凑，但是有几个变量因此失去了和其他变量之间的相关性，所以直接粗暴的对所有数值型变量做异常值抹平可能是有问题的，让我们先搁置争议，继续往下建模尝试。

四、建模分析

#=======================建模前数据准备 ===================
# 5折交叉验证
train_control <- trainControl(method = 'cv', number = 5)#分层抽样 
set.seed(42) # 设置随机种子# 根据数据的因变量进行7:3的分层抽样
index <-createDataPartition(data$NSP, p = 0.7, list = FALSE) 
index <- as.vector(index）traindata <- data[index,] # 提取数据中的index所对应行索引的数据作为训练集
testdata <- data[-index,] # 其余的作为测试集# 对数据进行标准化
standard <- preProcess(traindata, method = c("center","scale"))
traindata_std <- predict(standard, traindata)
testdata_std <- predict(standard, testdata)#========================== 1、回归树 ======================
#建立模型
rpart_model <- train(NSP~ ., data = traindata_std, trControl = train_control, method = 'rpart')#模型预测
rpart_pred <- predict(rpart_model, testdata[-23])# 建立混淆矩阵(精度0.9194)
rpart_result <- confusionMatrix(rpart_pred, testdata_std$NSP) 
rpart_result#可视化变量重要性
dev.new()
plot(varImp(rpart_model))#可视化条件推断树
plot(as.party(rpart_model$finalModel))#========================= 2、随机森林==========================
## 建立随机森林模型进行预测，并可视化变量重要性
rf_model <- randomForest(NSP ~., data = traindata_std, importance =T)
#预测
rf_pred <- predict(rf_model, testdata_std[-23], type = 'class')
#混淆矩阵
rf_result <- confusionMatrix(rf_pred, testdata_std$NSP)
rf_result   #精度0.981
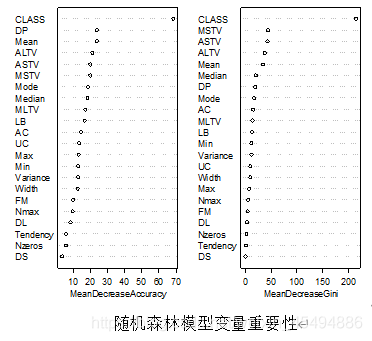
varImpPlot(rf_model)                 # 可视化变量重要性# =======================3、朴素贝叶斯 ========================
nb_model <- train(NSP ~., data = traindata_std,trControl = train_control,
method = 'nb')
nb_pred <- predict(nb_model, testdata_std[-23])
nb_result <- confusionMatrix(nb_pred, testdata_std$NSP) 
nb_result  #精度0.8626 #=======================4、支持向量机 =====================
svm_model <- svm(NSP~.,data = traindata_std, kernel = 'radial')
svm_pred <- predict(svm_model, testdata_std[-23], type = 'response')
svm_result <- confusionMatrix(svm_pred, testdata_std$NSP) 
svm_result  #精度0.9779#========================= 5、knn ==============================
## knn交叉验证
results = c()      # 创建一个空向量
for(i in 3:10) {set.seed(1234)knn_pred <- knn(traindata_std[-23],testdata_std[-23], traindata_std$NSP, i)Table <- table(knn_pred, testdata_std$NSP)accuracy <- sum(diag(Table))/sum(Table) #diag()提取对角线上的值results <- c(results, accuracy)
}# 画出精度-vs-N图
dev.new()
plot(x = 3:10, y = results,type = 'b', col = 'blue', xlab = 'k', ylab = 'accuracy')#当k=5时，预测
knn_pred <- knn(train =
traindata_std[-23], test = testdata_std[-23], cl = traindata_std$NSP, k = 5)#模型结果
knn_result <- confusionMatrix(knn_pred , testdata_std$NSP)
knn_result#==================== 6、bp神经网络 =====================
#数据准备
set.seed(1234)
#独热变量
dummy_train <- model.matrix(~Tendency+CLASS,traindata_std)
traindata_std1 <- cbind(traindata_std[,1:20],dummy_train[,-1])traindata_std1$one = traindata_std$NSP == 1
traindata_std1$two = traindata_std$NSP == 2
traindata_std1$three = traindata_std$NSP == 3traindata_std1#建模
bp_modal <- neuralnet(one+two+three ~.,data=traindata_std1,threshold=0.01,stepmax=100000,err.fct="ce",linear.output=F,hidden=5)#画出拓扑结构
dev.new()
plot(bp_modal)#模型结果
bp_modal$result.matrix
bp_modal$net.result#测试集上计算性能
dummy_test <- model.matrix(~Tendency+CLASS,testdata_std)testdata_std1 <- cbind(testdata_std[,1:20],dummy_test[,-1])testdata_std1$one = testdata_std$NSP == 1
testdata_std1$two = testdata_std$NSP == 2
testdata_std1$three = testdata_std$NSP == 3#看下数据
testdata_std1 %>%
glimpse()bp_result <- compute(bp_modal,testdata_std1)#混淆矩阵
predict.table = table(testdata_std$NSP,bp_pred)
predict.table#计算预测值
bp_pred =c("one","two","three")[apply(bp_result$net.result,
1, which.max)] %>% as.data.frame()bp_pred_num <- bp_pred %>% mutate(pred=case_when(bp_pred=='one' ~ 1,bp_pred=='two' ~ 2,bp_pred=='three' ~ 3,))bp_pred1 <- bp_pred_num[[2]] %>% as.factor()#模型结果
bp_cm <- confusionMatrix(bp_pred1,testdata_std$NSP)
bp_cm

结果解读：
在这里插入图片描述
决策树的变量重要性和决策规则绘制如下。
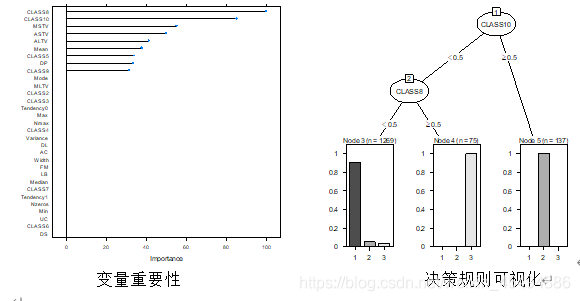
在这里插入图片描述在这里插入图片描述
将变量重要性绘图如下，可以尝试挑选重要变量再次建模，就本模型来说，精度等指标已经足够好，故不再做过多尝试。
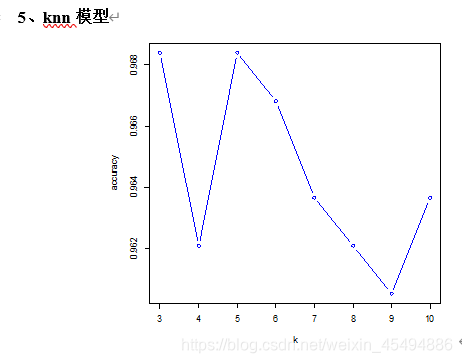
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
上图为交叉验证选择n的精度变化图，从图中可以看出当n取3或5时，分类精度最高，这里取n=5时进行验证。
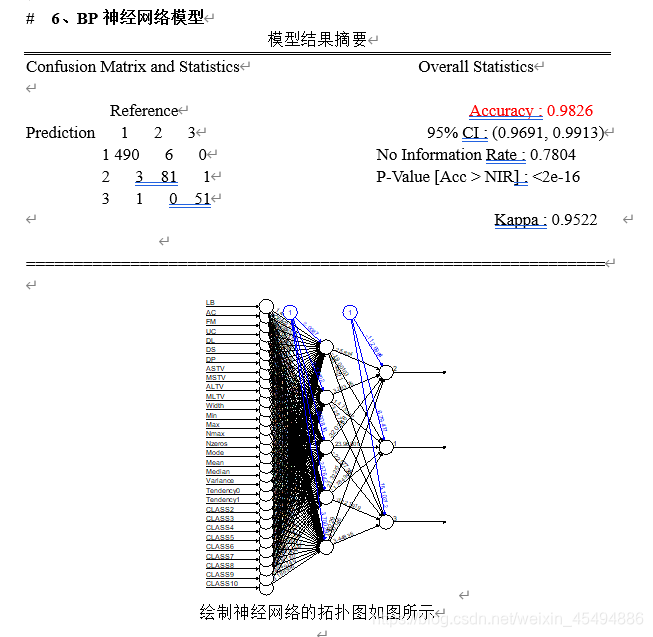
在这里插入图片描述
在这里插入图片描述

五、模型评价

#======================== AUC ========================
rpart_roc <- multiclass.roc(testdata_std$NSP,as.numeric(rpart_pred),direction = "<") 
rf_roc <- multiclass.roc(testdata_std$NSP, as.numeric(rf_pred) ,direction = "<") 
nb_roc <- multiclass.roc(testdata_std$NSP, as.numeric(nb_pred),direction = "<") 
svm_roc <- multiclass.roc(testdata_std$NSP, as.numeric(svm),direction = "<")
knn_roc <- multiclass.roc(testdata_std$NSP, as.numeric(knn_pred),direction = "<")
bp_roc <- multiclass.roc(testdata_std$NSP,as.numeric(bp_pred1),direction = "<")#AUC值比较
rpart_roc #0.7776
rf_roc #0.9796
nb_roc # 0.7797
svm_roc #0.9552
knn_roc #0.941
bp_roc #0.9835

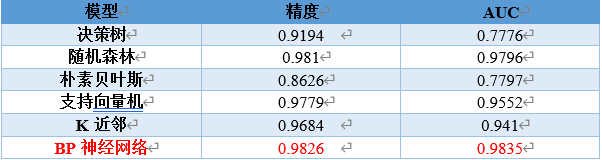
在这里插入图片描述
从模型结果来看，单隐层BP神经网络的准确率和AUC值均最高，在不要求模型解释性的情况下，是解决NSP分类的最佳选择。

这篇关于基于R语言的机器学习多分类任务（决策树、随机森林、朴素贝叶斯、支持向量机、KNN、BP神经网络）——UCL胎心宫缩监护数据（CTG.xls）预测分析的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/369527。

相关文章

openCV中KNN算法的实现

openCV中KNN算法的实现

《openCV中KNN算法的实现》KNN算法是一种简单且常用的分类算法,本文主要介绍了openCV中KNN算法的实现,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的... 目录KNN算法流程使用OpenCV实现KNNOpenCV 是一个开源的跨平台计算机视觉库，它提供了各
阅读更多...
Go 语言中的select语句详解及工作原理

Go 语言中的select语句详解及工作原理

《Go语言中的select语句详解及工作原理》在Go语言中,select语句是用于处理多个通道（channel）操作的一种控制结构,它类似于switch语句,本文给大家介绍Go语言中的select语... 目录Go 语言中的 select 是做什么的基本功能语法工作原理示例示例 1：监听多个通道示例 2：带
阅读更多...
C语言函数递归实际应用举例详解

C语言函数递归实际应用举例详解

《C语言函数递归实际应用举例详解》程序调用自身的编程技巧称为递归,递归做为一种算法在程序设计语言中广泛应用,：本文主要介绍C语言函数递归实际应用举例的相关资料,文中通过代码介绍的非常详细,需要的朋... 目录前言一、递归的概念与思想二、递归的限制条件 三、递归的实际应用举例（一）求 n 的阶乘（二）顺序打印
阅读更多...
Python中随机休眠技术原理与应用详解

Python中随机休眠技术原理与应用详解

《Python中随机休眠技术原理与应用详解》在编程中,让程序暂停执行特定时间是常见需求,当需要引入不确定性时,随机休眠就成为关键技巧,下面我们就来看看Python中随机休眠技术的具体实现与应用吧... 目录引言一、实现原理与基础方法1.1 核心函数解析1.2 基础实现模板1.3 整数版实现二、典型应用场景2
阅读更多...
C语言中的数据类型强制转换

C语言中的数据类型强制转换

《C语言中的数据类型强制转换》：本文主要介绍C语言中的数据类型强制转换方式,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录C语言数据类型强制转换自动转换强制转换类型总结C语言数据类型强制转换强制类型转换：是通过类型转换运算来实现的，主要的数据类型转换分为自动转换
阅读更多...
利用Go语言开发文件操作工具轻松处理所有文件

利用Go语言开发文件操作工具轻松处理所有文件

《利用Go语言开发文件操作工具轻松处理所有文件》在后端开发中,文件操作是一个非常常见但又容易出错的场景,本文小编要向大家介绍一个强大的Go语言文件操作工具库,它能帮你轻松处理各种文件操作场景... 目录为什么需要这个工具？核心功能详解1. 文件/目录存javascript在性检查2. 批量创建目录3. 文件
阅读更多...
C语言实现两个变量值交换的三种方式

C语言实现两个变量值交换的三种方式

《C语言实现两个变量值交换的三种方式》两个变量值的交换是编程中最常见的问题之一,以下将介绍三种变量的交换方式,其中第一种方式是最常用也是最实用的,后两种方式一般只在特殊限制下使用,需要的朋友可以参考下... 目录1.使用临时变量（推荐）2.相加和相减的方式（值较大时可能丢失数据）3.按位异或运算1.使用临时
阅读更多...
使用C语言实现交换整数的奇数位和偶数位

使用C语言实现交换整数的奇数位和偶数位

《使用C语言实现交换整数的奇数位和偶数位》在C语言中,要交换一个整数的二进制位中的奇数位和偶数位,重点需要理解位操作,当我们谈论二进制位的奇数位和偶数位时,我们是指从右到左数的位置,本文给大家介绍了使... 目录一、问题描述二、解决思路三、函数实现四、宏实现五、总结一、问题描述使用C语言代码实现：将一个整
阅读更多...
C语言字符函数和字符串函数示例详解

C语言字符函数和字符串函数示例详解

《C语言字符函数和字符串函数示例详解》本文详细介绍了C语言中字符分类函数、字符转换函数及字符串操作函数的使用方法,并通过示例代码展示了如何实现这些功能,通过这些内容,读者可以深入理解并掌握C语言中的字... 目录一、字符分类函数二、字符转换函数三、strlen的使用和模拟实现3.1strlen函数3.2st
阅读更多...
Go语言中最便捷的http请求包resty的使用详解

Go语言中最便捷的http请求包resty的使用详解

《Go语言中最便捷的http请求包resty的使用详解》go语言虽然自身就有net/http包,但是说实话用起来没那么好用,resty包是go语言中一个非常受欢迎的http请求处理包,下面我们一起来学... 目录安装一、一个简单的get二、带查询参数三、设置请求头、body四、设置表单数据五、处理响应六、超
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2