本文主要是介绍P02114200祁琪,P02114213杨佳儒,P02114193魏子昂,P02114105江琦,P02114208辜子豪——信息熵可加性和递增性的证明研究与拓展,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1.预备知识
2.证明过程
2.1.对于信息熵可加性的证明
2.2.对于信息熵递增性的证明
3.拓展
3.1可加性的拓展
3.2递增性的扩展
3.3信息粒和决策树
3.3.1.信息粒
3.3.2.信息熵与信息粒
3.3.3.决策树
3.3. 4.信息粒与决策树
3.3.5.结论
4.总结
1.预备知识
信息熵(information entropy)是信息论的基本概念。描述信息源各可能事件发生的不确定性。20世纪40年代,香农(C.E.Shannon)借鉴了热力学的概念,把信息中排除了冗余后的平均信息量称为“信息熵”,并给出了计算信息熵的数学表达式。信息熵的提出解决了对信息的量化度量问题。
信息是个很抽象的概念。人们常常说信息很多,或者信息较少,但却很难说清楚信息到底有多少。比如一本五十万字的中文书到底有多少信息量。
信息论之父克劳德·艾尔伍德·香农第一次用数学语言阐明了概率与信息冗余度的关系。
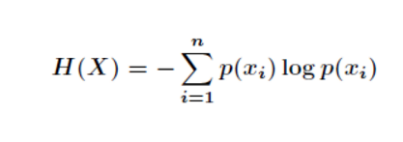
其中,x表示随机变量,与之相对应的是所有可能输出的集合,定义为符号集,随机变量的输出用x表示。P(x)表示输出概率函数。变量的不确定性越大,熵也就越大,把它搞清楚所需要的信息量也就越大. 信息熵《博弈圣经》 信息熵:信息的基本作用就是消除人们对事物的不确定性。多数粒子组合之后,在它似像非像的形态上押上有价值的数码,具体地说,这就是一个在博弈对局中信息混乱的现象。香农指出,它的准确信息量应该是-(p1*log(2,p1) + p2 * log(2,p2) + ... +p32 *log(2,p32)), 信息熵 其中,p1,p2 , ...,p32 分别是这 32 个球队夺冠的概率。香农把它称为“信息熵” (Entropy),一般用符号 H 表示,单位是比特。有兴趣的读者可以推算一下当 32 个球队夺冠概率相同时,对应的信息熵等于五比特。有数学基础的读者还可以证明上面公式的值不可能大于五。
对于任意一个随机变量 X(比如得冠军的球队),它的熵定义如下:变量的不确定性越大,熵也就越大,把它搞清楚所需要的信息量也就越大。信息熵是信息论中用于度量信息量的一个概念。一个系统越是有序,信息熵就越低;反之,一个系统越是混乱,信息熵就越高。所以,信息熵也可以说是系统有序化程度的一个度量。熵的概念源自热物理学。
2.证明过程
2.1.对于信息熵可加性的证明
H(X,Y)=H(X)+H(Y/X),当X、Y相互独立时,H(X,Y)=H(X)+H(Y)。
如果考虑概率的形式,设X的概率分布为(P1,P2,…Pn),已知X的情况下Y的条件概率为P(Y=yj/X=xi)=pij,则可加性表示为:

利用Matlab证明熵的可加性:
首先,需要定义两个独立系统的熵分别为S1和S2。然后,将这两个系统组合成一个大系统,其熵为S。利用熵的定义式和熵的可加性公式,即S=S1+S2,证明熵的可加性。
代码如下:
% 定义两个独立系统的熵
S1 = 1.5;
S2 = 2.0;
% 计算这两个系统组合成的大系统的熵
S = S1 + S2;
% 验证熵的可加性是否成立
if abs(S - (S1 + S2)) < eps
disp('熵的可加性成立');
else
disp('熵的可加性不成立');
End这段代码中,eps表示机器精度,用于判断两个浮点数是否相等。如果输出结果为“熵的可加性成立”,则说明熵的可加性在这两个系统中成立。
2.2.对于信息熵递增性的证明
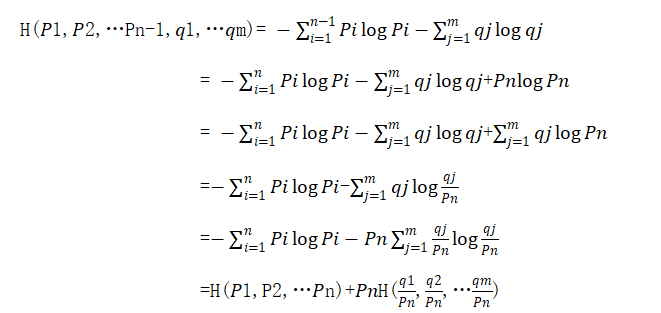
该性质表明,若信源X中有一元素划分成m个符号,而这m个符号的概率之和等于原元素的概率,则新元素的熵会增加。熵增加了的一项是由于划分而产生的不确定性。
3.拓展
3.1可加性的拓展

3.2递增性的扩展

3.3信息粒和决策树
前言:
信息熵是信息系统不确定程度的度量,熵越大,系统的不确定性也越大,确定它需要的信息量也越大。 在一个信息系统中,信息熵经常与信息粒和决策树相联系。
3.3.1.信息粒
信息粒化这一概念最早是由Lotfi A. Zadeh(L.A. Zadeh)教授提出的.信息粒化就是将一个整体分解为一个个的部分进行研究,每个部分为一个信息粒. Zadeh教授指出:信息粒就是一些元素的集合,这些元素由于难以区别、或相似、或接近或某种功能而结合在一起.
信息粒作为信息的表现形式在我们的周围是无所不在的,它是人类认识世界的一个基本概念.人类在认识世界时往往将一部分相似的事物放在一起作为一个整体研究它们所具有的性质或特点,实际上,这种处理事物的方式就是信息粒化.而所研究的“整体”就称为信息粒. 例如:时间信息粒有年、月、日、时等.从时间信息粒中可以看出信息粒在本质上是分层次的,一种信息粒可以细化为更“低”一层次的信息粒。
3.3.2.信息熵与信息粒

3.3.3.决策树
决策树是一个预测模型,它代表的是对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象,而每个分叉路径则代表某个可能的属性值,而每个叶节点则对应从根节点到该叶节点所经历的路径所表示的对象的值。
从数据产生决策树的机器学习技术叫做决策树学习,通俗说就是决策树。
一个决策树包含三种类型的节点:
- 决策节点:通常用矩形框来表示
- 机会节点:通常用圆圈来表示
- 终结节点:通常用三角形来表示
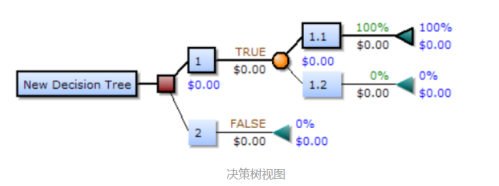
3.3. 4.信息粒与决策树
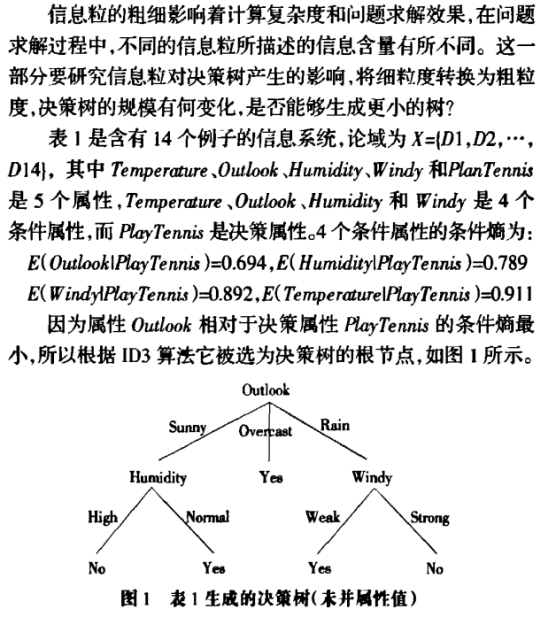
3.3.5.结论
不同的信息粒所描述的信息含量有所不同.信息粒的粗细影响着计算复杂度和问题求解效果.在研究了粗粒度和细粒度对信息熵和条件熵及决策树的影响,得出了结论:粗信息粒的信息熵不小于细信息粒的信息熵及条件熵,细信息粒下选取扩展属性产生的决策树优于粗信息粒下选取扩展属性生成的决策树。
4.总结
信息熵性质的研究是香农信息论在理论与编码应用方面的重要内容之一。本调研证明了递增性和可加性,并在此基础上拓展了可加性和递增性,并介绍了信息粒和决策树的基本性质。
调研成员:
P02114200祁琪,P02114213杨佳儒,P02114193魏子昂,P02114105江琦,P02114208辜子豪
指导老师:
李丽萍
这篇关于P02114200祁琪,P02114213杨佳儒,P02114193魏子昂,P02114105江琦,P02114208辜子豪——信息熵可加性和递增性的证明研究与拓展的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






