减治法（引例中位数、查找问题：折半二叉选择、排序问题：堆排序、组合问题：淘汰赛冠军问题假币问题）

分治法需要对分解的子问题分别求解，再对子问题进行合并，减治法只对一个子问题求解，并且不需要进行解的合并。减治法的效率更好。

*时间复杂性为log2n

*思路：如果n=1,返回a的值；n是偶数且n>1，把该问题的规模减半，计算a^n/2的值；n是奇数且n>1，先利用偶指数的规则计算a^(n-1)，再把结果乘以a

            a   n=1

a^n=    (a^n/2)^2        n>1且n是偶数

            (a^n-1/2)^2*a  n>1且n是奇数

例题

减治法求两个序列的中位数

#include<iostream>
using namespace std;int SearchMid(int A[],int B[],int n){//初始化两个序列的上下界int s1=0,e1=n-1,s2=0,e2=n-1;int mid1,mid2;while(s1<e1&&s2<e2){ //循环--直到区间只有一个元素 mid1=(s1+e1)/2; //序列A的中位数下标 mid2=(s2+e2)/2; //序列B的中位数下标 if(A[mid1]==B[mid2]){ //当a=b时 返回a 算法结束 return A[mid1];}if(A[mid1]<B[mid2]){ //a<b 舍弃a之前的元素舍弃b之后的元素 (a,b)之间 if((s1+e1)%2==0) s1=mid1; //头指针变成mid开始 else s1=mid1+1;e2=mid2; //尾指针变成中间部分 }if(A[mid1]>B[mid2]){ //a>b 舍弃a之后的元素舍弃b之前的元素(b,a)之间 if((s2+e2)%2==0) s2=mid2;else s2=mid2+1;e1=mid1;}}//返回较小者if(A[s1]<B[s2]){return A[s1];} else{return B[s2];}
}int main(){int n; //长度cout<<"请输入数组长度："<<endl;cin>>n;int A[n],B[n];cout<<"请输入A数组："<<endl;for(int i=0;i<n;i++){cin>>A[i];} cout<<"请输入B数组："<<endl;for(int i=0;i<n;i++){cin>>B[i];}int res=0;res=SearchMid(A,B,n);cout<<"中位数是："<<res<<endl;return 0;}

查找问题 

 折半查找

        折半查找与待查值每比较依次，根据比较结果是的查找的区间减半

        *前提：序列有序，若序列无序，需要先进行排序

#include<iostream>
using namespace std;int BinSearch(int r[],int n,int k){int low=0,high=n-1;int mid;while(low<=high){mid=(low+high)/2;if(k<r[mid]){high=mid-1;}else if(k>r[mid]){high=mid+1;}else{return mid;}}return -1; //查找失败，返回-1 
}int main(){int n;cout<<"请输入序列长度:"<<endl;cin>>n; int a[n];cout<<"请输入序列："<<endl;for(int i=0;i<n;i++){cin>>a[i];}int k;cout<<"请输入待查找的值："<<endl;cin>>k;int res;res=BinSearch(a,n,k);cout<<"您所查找的值在"<<res<<"下标位置"<<endl; return 0;
}

二叉查找树（有bug）

        若左子树不为空，左子树上所有结点小于根结点；右子树不为空，右子树上所有结点大于根节点；左右子树都是二叉排序树。

        #在一个无序序列中执行查找操作，可以将无序序列建立一个二叉查找树，然后再二叉查找树中查找值为k的记录。若成功，返回记录k的存储地址；失败，返回空。

#include<iostream>
using namespace std;
//用二叉链表存储二叉查找树，设root为指向二叉链表的跟指针
struct BiNode{int data;BiNode *lchild,*rchild;
}; //二叉树存在以后，二叉树的查找算法 
BiNode *searchBST(BiNode *root,int k){if(root==NULL) //如果二查找树为空，查找失败{return NULL; } if(root->data==k){ //如果相等 查找成功return root; }else if(root->data<k){ //向左边递归查找 查找左子树 return searchBST(root->lchild,k); }else if(root->data>k){ //向右递归查找 查找右子树return searchBST(root->rchild,k); }
}//在执行查找操作之前首先需要建立无序二叉查找树
BiNode *InsertBST(BiNode *root,int data){if(root==NULL){//首先 为data申请一个新的结点 root=new BiNode;root->data=data;//其次，让该结点成为叶子结点root->lchild=root->rchild=NULL;return root; }if(data<=root->data){//插入在左子树 root->lchild=InsertBST(root->lchild,data);}else if(data>root->data){//插入在右子树 root->rchild=InsertBST(root->rchild,data);}return root;
}//将无序序列建立一个二叉查找树
BiNode *CreateBST(int a[],int n){BiNode *T=NULL;for(int i=0;i<n;i++){T=InsertBST(T,a[i]); //在二叉查找树中插入元素a[i] }return T;
} int main(){int n;cout<<"请输入待排序的结点个数："<<endl;cin>>n;int a[n];BiNode *T=new BiNode();cout<<"请输入每个结点："<<endl;for(int i=0;i<n;i++){cin>>a[i];T=CreateBST(a,n);}int k;cout<<"请输入待查找的值"<<endl;cin>>k;cout<<"查找值就在"; cout<<searchBST(T,k)<<"位置";
}

 选择问题：寻找T的第k小元素的问题

#include<iostream>
using namespace std;int Partition(int r[],int low,int high){//对数据进行划分 //无序数组 左边 右边 左小右大int i=low,j=high;while(i<j){//扫描右侧 while(i<j&&r[i]<r[j]) j--; if(i<j){//如果左边比右边的大 就交换 （左小右大）int temp=r[i];r[i]=r[j];r[j]=temp;i++; //移动左边的指针 }//扫描左侧 while(i<j&&r[i]<r[j]) i++;if(i<j){//如果右边比左边的小 就交换 保证左边是小的 右边是大的int temp=r[i];r[i]=r[j];r[j]=temp; j--; //右边的指针向左移动 }}//循环结束i=j时候//返回i的坐标就是中间值 return i;
}int SelectMink(int r[],int k,int low,int high)
{//选择问题的实现 k是待查找的数 int s;//s是要找的轴值 （位置坐标） s= Partition(r,low,high);//如果在中间，就直接返回找到了 ！查找成功 if(s==k){return r[s];}//如果k<r[i] 在左边递归查找else if(k<s){return SelectMink(r,k,low,s-1);}//如果k>r[i] 在右边递归查找 else{return SelectMink(r,k,s+1,high);}
}int main(){cout<<"请输入数据总数："<<endl;int n;cin>>n;int r[n];cout<<"请输入数据:"<<endl;for(int i=0;i<n;i++){cin>>r[i];}int k; //传入的是数据的位置坐标 cout<<"请输入想查找的第k个元素："<<endl;cin>>k;k=k-1; int low=0,high=n-1;int res=SelectMink(r,k,low,high); //要找的是排行老四位置的数是多少 cout<<res; 
}

排序问题

插入排序：用插入排序的方法对一个记录序列进行升序排列。

*依次将待排序序列中的每一个记录插入到一个已经排好序的序列中，直到所有记录都排好序

#include<iostream>
using namespace std;
/*
void InsertSort(int r[],int n){int i,j=0; //待排序记录序列存储在r[1]~r[n]中 for(i=2;i<=n;i++){ //从第二个记录开始执行插入操作if(r[i]<r[i-1]){r[0]=r[i]; //暂存待插记录，设置哨兵for(j=i-1;r[j]>r[0];j--){ //寻找插入位置r[j+1]=r[j]; //记录后移 }} r[j+1]=r[0]; }
}*/void InsertSort(int* arr, int n)
{for (int i = 0; i < n - 1; ++i){//记录有序序列最后一个元素的下标int end = i;//待插入的元素int tem = arr[end + 1];//单趟排while (end >= 0){//比插入的数大就向后移if (tem < arr[end]){arr[end + 1] = arr[end];end--;}//比插入的数小，跳出循环else{break;}}//tem放到比插入的数小的数的后面arr[end  + 1] = tem;//代码执行到此位置有两种情况://1.待插入元素找到应插入位置（break跳出循环到此）//2.待插入元素比当前有序序列中的所有元素都小（while循环结束后到此）}
}
int main(){int n;cout<<"请输入个数："<<endl;cin>>n;int r[n];cout<<"请输入数组："<<endl;for(int i=0;i<n;i++){cin>>r[i];}InsertSort(r,n);cout<<"排序后的结果是："<<endl;for(int i=0;i<n;i++){cout<<r[i]<<" ";}return 0;
}

堆排序 

*1）筛选法：整成大（小）顶堆

2）将堆顶元素和堆的最后一个元素进行交换，重复步骤1

#include<iostream>
using namespace std;//首先将无序序列调整成堆，由于叶子结点均可以看作是堆，因此，可以从编号最大的分支节点直至根节点反复调用筛选法 
void SiftHeap(int r[],int k,int n){//筛选法 输入的数组 数组规模 int i,j,temp;//i:要筛选的结点 j:i的左孩子i=k;j=2*i+1;while(j<n){if(j<n-1&&r[j]<r[j+1]) j++; //比较i的左右孩子 j<n-1是为了保证不会出界 if(r[i]>r[j]) break; //结束比较 根节点已经大于左右孩子中的较大者 else{temp=r[i]; //交换 r[i]=r[j];r[j]=temp;i=j; //被筛选结点位于原来结点j的位置 j=2*i+1; //j得继续找做孩子 }		 } 
}void HeapSort(int r[],int n){//堆排序 变成从小到大的输出顺序了 int i,temp;for(i=(n-1)/2;i>=0;i--){ //从最后一个非叶结点开始 SiftHeap(r,i,n); //调整成堆 }for(i=1;i<=n-1;i++){//重复执行移走对顶及重建堆的操作temp=r[0];r[0]=r[n-i];r[n-i]=temp;SiftHeap(r,0,n-i);//只需要调整根节点 }
}//堆排序 
int main(){int n;cout<<"请输入数据总数:";cin>>n;int a[n];cout<<"请输入数组:";for(int i=0;i<n;i++){cin>>a[i];} HeapSort(a,n);for(int i=0;i<n;i++){cout<<a[i]<<endl;;}return 0;
}

组合问题

淘汰赛冠军问题

char Game(int n,char r[]){int i=n;while(i>1){ //比赛直到剩余1人即为冠军i=i/2;for(int j=0;j<i;i++){if(Comp(r[j+1],r[j])) //模拟两位选手比赛 若mem1获胜返回1 //若mem2获胜返回0 r[j]=r[j+1]; //将胜者存入r[j]中 } }return r[0]; //返回冠军 
}

 实例：洛谷

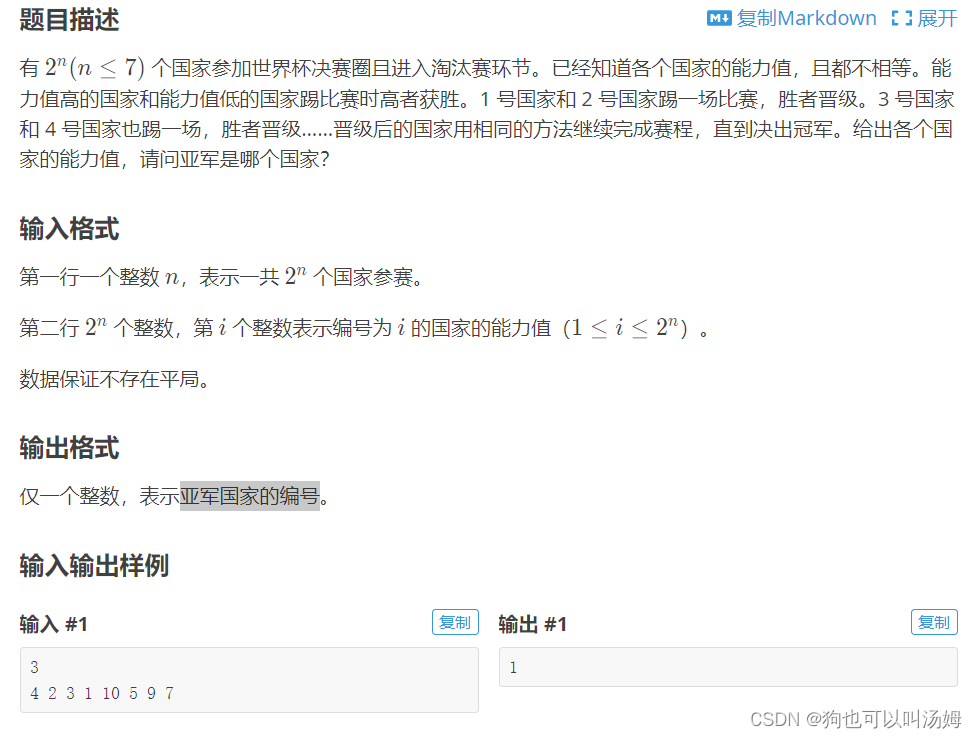
#include <iostream>
using namespace std;
struct node
{int num,grade;//编号，能力值
} a[130];//最多为2^7，即128，故设数组130
int main()
{int n,m = 1;cin>>n;for(int i = 1;i <= n;i++) m *= 2;//共有z^n支队伍for(int i = 1;i <= m;i++){a[i].num = i;//记录编号 cin>>a[i].grade;}while(m > 2)//循环条件 {int q = 0;//初始化 for(int i = 1;i <= m;i += 2)//每次+2，两两比较的缘故 {if(a[i].grade > a[i + 1].grade) a[++q] = a[i]; //q为计数用else a[++q] = a[i + 1];} m /= 2;//每次减少一半，a数组的前一半便是晋级的队伍}//最后只剩下两支队伍，比较后输出亚军的编号，即能力值较小的队伍 if(a[1].grade > a[2].grade) cout<<a[2].num<<endl;else cout<<a[1].num<<endl;return 0; 
} 

 假币问题

add1存储第一组硬币的重量和

add2存储第二组硬币的重量和

add3存储第三组硬币的重量和

add1<add2 在第一组中

add2<add1 在第二组中

add1=add2 在第三组中

#include <iostream>
using namespace std;
const int N=8;int a[N]={2,2,1,2,2,2,2,2}; //假币的重量是1 int Coin(int low,int high,int n){int i,num1,num2,num3; //分别存储三个硬币的个数int add1=0,add2=0;//存储前两组硬币的重量和if(n==1){return low+1; //递归结束条件 }if(n%3==0){//如果恰好可以被整除num1=n/3; num2=n/3;}else{num1=n/3+1; //前两组向上取整 num2=n/3+1;}num3=n-num1-num2; //不管是那种情况，第三种的个数都是这也//计算重量for(i=0;i<num1;i++){add1=add1+a[low+i];} for(i=num1;i<num1+num2;i++){add2=add2+a[low+i];}//两组比较大小if(add1<add2){//在第一组中 return Coin(low,low+num1-1,num1); } else if(add1>add2){//在第二组中return Coin(low+num1,low+num1+num2-1,num2); } else{//在第三组中return Coin(low+num1+num2,high,num3); } 
} int main()
{int n;n=Coin(0,7,8);cout<<n;
}