深度学习 GNN图神经网络（四）线性回归之ESOL数据集水溶性预测

一、前言

本文旨在使用化合物分子的SMILES字符串进行数据模型训练，对其水溶性的值进行预测。

之前的文章《深度学习 GNN图神经网络（三）模型思想及文献分类案例实战》引用的Cora数据集只有一张图，属于图神经网络的节点分类问题。本文介绍的是多图批量训练的线性回归问题，在文章最后也讨论了图分类问题。

二、ESOL数据集

本文使用的是ESOL数据集，在文章《如何将化学分子SMILES字符串转化为Pytorch图数据结构——ESOL分子水溶性数据集解析》中有详细介绍，在此不作详述。

三、加载数据集

from torch_geometric.datasets import MoleculeNetdataset = MoleculeNet(root="data", name="ESOL")print('num_features:',dataset.num_features)
print('num_classes:',dataset.num_classes)
print('num_node_features',dataset.num_node_features)
print("size:", len(dataset))d=dataset[10]
print("Sample:", d)
print("Sample y:", d.y)
print("Sample num_nodes:",d.num_nodes)
print("Sample num_edges:",d.num_edges)

这里可以得到数据集的一些基本信息：

num_features: 9
num_classes: 734
num_node_features 9
size: 1128
Sample: Data(x=[6, 9], edge_index=[2, 12], edge_attr=[12, 3], smiles='O=C1CCCN1', y=[1, 1])
Sample y: tensor([[1.0700]])
Sample num_nodes: 6
Sample num_edges: 12

四、数据拆分

将数据集拆分为训练数据和测试数据：

from torch_geometric.loader import DataLoader
data_size = len(dataset)
batch_size = 128
train_data=dataset[:int(data_size*0.8)]
test_data=dataset[int(data_size*0.8):]train_loader = DataLoader(train_data, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(test_data, batch_size=len(test_data))

五、构造模型

import torch
import torch.nn as nn
from torch_geometric.nn import GCNConv
import matplotlib.pyplot as plt
from torch_geometric.nn import global_mean_pooldevice = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")hidden_channels = 64class GNN(nn.Module):def __init__(self):# 初始化Pytorch父类super().__init__()self.conv1=GCNConv(dataset.num_node_features, hidden_channels)self.conv2=GCNConv(hidden_channels, hidden_channels)self.conv3 = GCNConv(hidden_channels, hidden_channels)self.conv4 = GCNConv(hidden_channels, hidden_channels)self.out = nn.Linear(hidden_channels, 1)# 创建损失函数，使用均方误差self.loss_function = nn.MSELoss()# 创建优化器，使用Adam梯度下降self.optimiser = torch.optim.Adam(self.parameters(), lr=0.005,weight_decay=5e-4)# 训练次数计数器self.counter = 0# 训练过程中损失值记录self.progress = []# 前向传播函数def forward(self, x, edge_index,batch):x=x.to(device)edge_index=edge_index.to(device)batch=batch.to(device)x=self.conv1(x, edge_index)x=x.relu()x=self.conv2(x, edge_index)x=x.relu()x=self.conv3(x, edge_index)x=x.relu()x=self.conv4(x, edge_index)x=x.relu()# 全局池化x = global_mean_pool(x, batch)  # [x, batch]out=self.out(x)return out# 训练函数def train(self, data):# 前向传播计算，获得网络输出outputs = self.forward(data.x.float(),data.edge_index,data.batch)# 计算损失值y=data.y.to(device)loss = self.loss_function(outputs, y)# 累加训练次数self.counter += 1# 每10次训练记录损失值if (self.counter % 10 == 0):self.progress.append(loss.item())# 每1000次输出训练次数   if (self.counter % 1000 == 0):print(f"counter={self.counter}, loss={loss.item()}")# 梯度清零, 反向传播, 更新权重self.optimiser.zero_grad()loss.backward()self.optimiser.step()# 测试函数def test(self, data):# 前向传播计算，获得网络输出outputs = self.forward(data.x.float(),data.edge_index,data.batch)# 把绝对值误差小于1的视为正确，计算准确度y=data.y.to(device)acc=sum(torch.abs(y-outputs)<1)/len(data.y)return acc# 绘制损失变化图def plot_progress(self):plt.plot(range(len(self.progress)),self.progress)

六、训练模型

model = GNN()
model.to(device)for i in range(1001):for data in train_loader:# print(data,'num_graphs:',data.num_graphs)model.train(data)

counter=1000, loss=1.4304862022399902
counter=2000, loss=0.9842458963394165
counter=3000, loss=0.27240827679634094
counter=4000, loss=0.23295772075653076
counter=5000, loss=0.38499030470848083
counter=6000, loss=1.470423698425293
counter=7000, loss=0.845589816570282
counter=8000, loss=0.15707021951675415

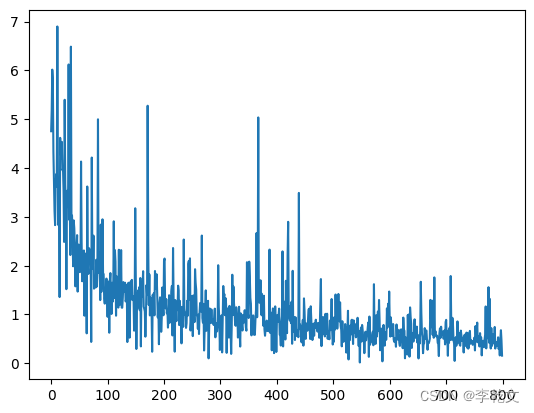
绘制损失值变化图：：

model.plot_progress()

七、测试结果

#torch.set_printoptions(precision=4,sci_mode=False) #pytorch不使用科学计数法显示for data in test_loader:acc=model.test(data)print(acc)

tensor([0.8186], device='cuda:0')

可以看到，预测值误差小于1的占了81.86%，效果还行。

八、分类问题

对于图分类问题，其实也差不多。只需要修改下Linear网络层：

self.out = Linear(hidden_channels, dataset.num_classes)

这样预测结果就会有num_classes个，取最大值的下标索引即可。
伪代码为：

pred=outputs.argmax(dim=1)
correct += int((pred == data.y).sum())

参考文献

[1] https://pytorch-geometric.readthedocs.io/en/latest/get_started/colabs.html
[2] https://zhuanlan.zhihu.com/p/504978470