本文主要是介绍【基于MRA:自适应高频融合和注入系数优化:Pansharpening】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Pansharpening Based on Adaptive High-Frequency Fusion and Injection Coefficients Optimization
(基于自适应高频融合和注入系数优化的全色锐化)
全色锐化的目的是将多光谱(MS)图像与全色(PAN)图像融合,以生成高空间分辨率的多光谱(HRMS)图像。针对传统的全色锐化方法没有充分考虑MS图像的信息,导致全色锐化结果中细节注入不准确和频谱失真的问题,提出了一种基于自适应高频融合和注入系数优化的全色锐化方法,能够获得准确的注入高频分量(HFC)和注入系数。首先,我们提出了一个多层次的锐化模型来增强MS图像的空间信息,然后从锐化的MS图像和PAN图像中提取HFCs。然后,设计了一种自适应融合策略,通过计算提取的HFC的相似性和差异性来获得准确的注入HFC。对于注入系数,我们提出了基于MS图像和PAN图像之间的空间和光谱关系的注入系数优化方案。最后,利用该注入系数将融合后的HFC注入到上采样后的MS图像中,得到HRMS图像
INTRODUCTIO
近年来,在环境监测、光谱分解、水质评价等应用中,对高精度卫星图像的需求越来越大。然而,受传感器的限制,高空间分辨率的多光谱(HRMS)图像很难通过单一传感器获得。该问题可以通过融合高空间分辨率全色(PAN)图像和高光谱分辨率多光谱(MS)图像以获得HRMS图像来解决。这个过程也被称为pansharpening。
在过去的几年中,已经开发了许多泛锐化方法,这些方法可以大致分为两类:传统方法和基于深度学习的方法。传统的方法包括基于成分替换(CS)的方法、基于多分辨分析(MRA)的方法和基于变分优化(VO)的方法。
在基于CS的方法中,首先将MS图像投影到另一空间中。然后,PAN图像被用来取代的空间信息的转换组件。最后通过逆变换得到HRMS图像。基于CS的代表性方法包括强度色调饱和度,主成分分析和Gram-Schmidt自适应方法。这些方法的优点是它们在空间信息方面是优秀的并且具有低计算复杂度。然而,缺点是它们容易出现频谱失真。
基于多分辨率分析的方法将源图像分解为不同尺度上的低频分量(LFC)和高频分量(HFC),然后按照一定的融合规则进行融合。最后,对融合后的分量进行逆变换,得到HRMS图像。常见的基于MRA的方法包括拉普拉斯变换、à trous小波变换(ATWT)、和基于强度调制的平滑滤波器。这种方法可以很好地保存光谱信息,但在增强空间信息方面仍存在一些缺陷。
基于VO的泛锐化方法包括两个步骤:能量函数的设计及其优化解。利用观测模型和稀疏表示等方法构造能量函数,然后利用优化算法进行求解,得到泛锐化图像。常见的基于VO的方法包括P+XS ,逆问题的正则化解,耦合非负矩阵分解和稀疏表示。虽然基于VO的方法的结果具有高精度,但计算成本相对较高。
近年来,深度学习在遥感图像处理领域取得了令人瞩目的成功。基于深度学习的方法通过学习遥感图像的特征来解决全息锐化问题。2016年,Masi等人提出了一种基于卷积神经网络的全息锐化方法。从那时起,更多基于深度学习的全息锐化方法被开发出来,包括深度残差网络、多尺度和多深度卷积神经网络和深度卷积神经网络。该方法善于从图像中学习复杂的特征,取得了较好的融合效果。然而,缺点是需要大量的训练样本和大量的训练时间,并且最优参数难以调整。
在上述分析的基础上,本文提出了一种基于自适应高频融合和注入系数优化的全锐化方法来获取高空间分辨率的MS图像,即HRMS图像。首先,利用多级锐化模型对MS图像进行锐化,并分别用ATWT和引导滤波得到锐化图像SI和PAN图像的高频分量HFC。其次,根据平移图像和锐化后的MS图像高频分量的异同和相似性,设计了一种自适应融合策略。在此基础上,提出了基于源图像空间和光谱信息的自适应注入系数。最后,按照设计的注入系数,将融合后的高频分量注入到上采样的MS(UPMS)图像中,得到HRMS图像。在IKONOS和Pléiade数据集上的实验表明,与现有的先进的全色锐化方法相比,我们的方法在主观和客观上都具有更好的性能,这证明了我们的方法的性能。
贡献
1)提出了一种基于自适应高频融合和注入系数优化的全色锐化方法,该方法能有效地保留全色图像的空间和光谱信息。
2)设计了一种多级锐化方案,能够很好地增强MS图像的空间信息。
3)根据PAN图像和锐化后的MS图像的根据PAN图像和锐化后的MS图像的HFC之间的差异和相似性,提出了一种自适应的融合策略。该策略能较好地保留MS和PAN图像的高频信息。
4)根据源图像的光谱和空间信息定义自适应注入系数,有效地控制HFC的注入,得到最终的HRMS图像。
RELATED WORKS
随着泛锐化研究的深入,注入模型在传统泛锐化方法中得到了广泛的应用。此外,基于注入模型的方法也逐渐取代了传统的泛锐化方法。在本节中,我们介绍了本文中使用的符号,并简要讨论了CS和MRA的详细注入模型。
Notation
取~M ∈ R M ∗ N ∗ K R^{M *N *K} RM∗N∗K作为与PAN图像大小相同的UPMS图像,其中M和N分别表示矩阵的行和列,K表示光谱带的数目。^M ∈ R M ∗ N ∗ K R^{M *N *K} RM∗N∗K表示全色锐化后的HRMS图像。I ∈ R M ∗ N R^{M *N} RM∗N表示强度分量,其通过~M的线性变换获得。通过将PAN图像的直方图与I匹配来计算P ∈ R M ∗ N R^{M *N} RM∗N。
CS-based Detail Injection Model
传统的基于CS的泛锐化方法是通过用PAN图像代替MS图像的空间分量来实现的。然而,Tu等人发现该方法可以以另一种方式实现,其通过计算PAN图像与MS图像的强度分量之间的差异来获得PAN图像的空间细节。因此,通过利用注入系数将所提取的空间细节注入到UPMS图像中来获得HRMS图像。基于CS的细节注入模型可以在没有空间变换的情况下实现,其定义如下:

MRA-based Detail Injection Model
与基于CS的细节注入模型不同,基于MRA的细节注入模型通过PAN图像与其LFC之间的差异来获得HFC。基于MRA的细节注入模型的公式定义如下: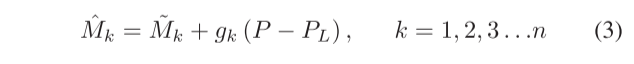
其中,PL表示P的LFC。Choi等人发现注入的HFC并不完全依赖PAN图像。此外,MS图像的HFC也与HRMS图像的HFC相关,这是从PAN图像中难以获得的。然而,MS图像的HFC对于后续结果很重要。因此,对HRMS的新定义如下: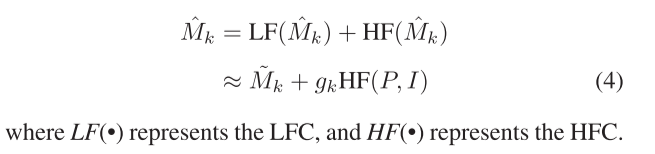
PROPOSED METHOD
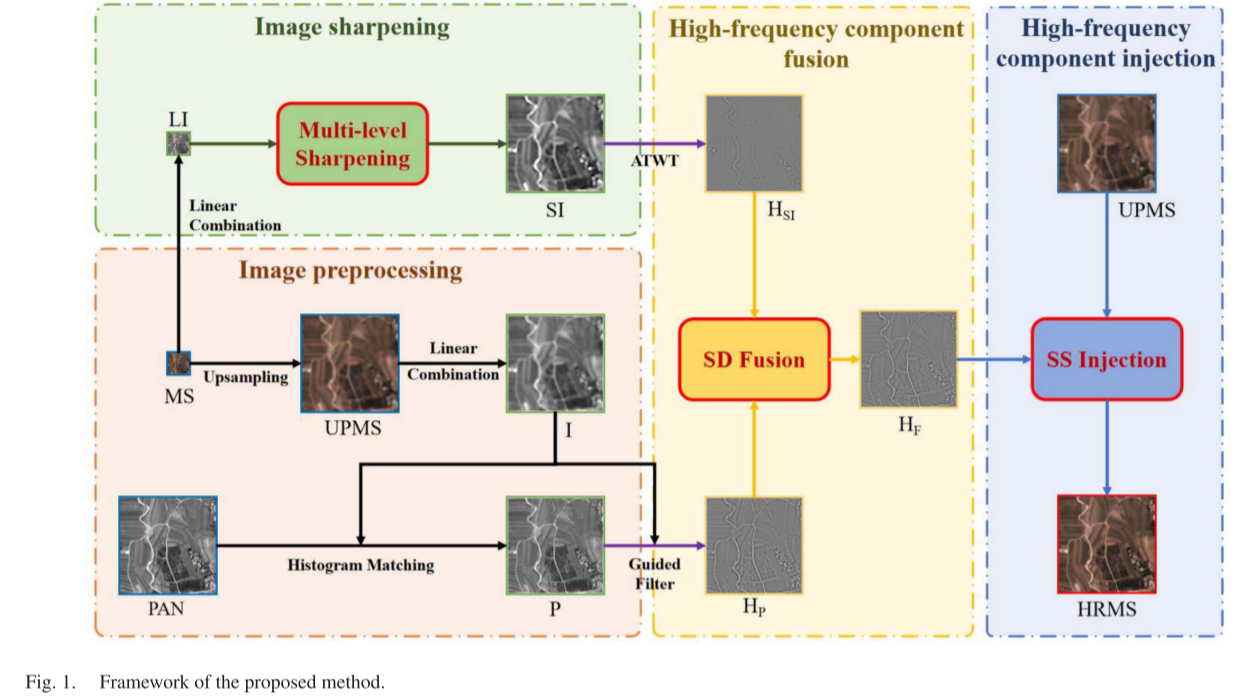
传统的基于MRA的注入模型一般是先融合源图像的高频细节,然后直接注入到UPMS图像中。与其他全色锐化方法不同,基于MRA的方法不仅能很好地保留图像的空间和光谱信息,而且计算复杂度相对较低。然而,由于MS图像中的空间信息是差的和模糊的,分解的HFC的直接融合在最终结果中导致伪影和模糊。因此,如何有效地提取和融合源图像的HFCs需要仔细考虑。此外,注入系数也需要仔细考虑。本文提出了一种新的泛锐化方法来解决上述问题,我们的方法的框架如图1所示,其过程描述如下。
1)对MS图像及其上采样版本进行预处理以分别获得线性组合分量(LI和I),并且通过对PAN图像和I分量使用直方图匹配来实现P分量。
2)提出了一种多级锐化的方法来锐化LI分量以获得SI。
3)分别通过ATWT和引导滤波器从SI和P中提取HFCs(HSI和HP)。
4)根据SI(HSI)和HP的高频相似性和差异性设计了一种高频融合规则,得到融合的高频(HF),表示为SD融合。
5)基于MS图像和PAN图像之间的空间和光谱关系来定义注入系数,这被称为SS注入。
6)融合的高频(HF)注入到UPMS图像通过使用获得的注入系数,以实现最终的HRMS图像。
Multilevel Sharpening
MS图像的空间信息较差,直接从MS图像中分解出的HFC较粗糙。因此,HFC的融合和注入在最终结果中导致模糊和伪影。解决这一问题的一个可行的方法是增强MS图像的空间信息。因此,为了减少伪影和增强空间信息,同时保持原始的空间信息,我们提出了一种多级锐化方法来增强MS图像的空间信息。
在多级锐化操作之前,对MS图像进行预处理以获得I和LI分量。首先,对MS图像进行上采样以获得~M。然后,I分量由 ~M的线性组合得到。类似地,通过MS图像的线性组合获得LI。最后,通过LI的多级锐化获得SI。
为了锐化MS图像,通过卷积算子提取MS图像的空间结构,然后通过将提取的空间结构与原始图像相加来获得SI。设计了一个3×3的算子核W,根据图像的周围信息锐化中心信息。由于PAN图像的尺寸是MS图像的四倍,并且直接以因子4对MS图像进行上采样难以获得满意的锐化结果。受图像金字塔的启发,我们将一个4的放大因子分为两个2的放大因子。因此,我们提出了一种多级锐化方法。多级锐化的具体步骤如算法1所示。该算法通过对LI图像的逐步锐化得到SI,改善了SI中MS图像的空间信息。

此外,为了说明多级锐化模型的有效性,我们的方法进行了比较,没有锐化过程的方法和直接上采样四次的方法。图2示出了在三个MS图像上的去锐化和锐化方法的比较结果。图2(a)示出了每个MS图像的分量L1。图2(b)-(d)显示了每种方法的结果的HFC。可以看出,锐化后的HFC图像细节更加清晰,而未锐化的HFCare图像细节模糊粗糙,而且多级锐化模型的效果优于直接上采样4次的效果,表明该锐化方法在增强空间信息方面具有优越的性能.
High-frequency Fusion Based on Similarity and Difference
在融合HFCs之前,需要单独提取源图像的HFCs。本文采用ATWT和引导滤波分别对MS图像和PAN图像进行滤波,以获得相应的HFC。ATWT是通过改进离散小波变换得到的,它具有许多优点,包括非正交性、移位不变性、非抽取性和冗余性。因此,为了更好地从MS图像中提取HFC,我们使用ATWT来获得HFC(HSI)。引导滤波类似于双边滤波,因为它也是一种边缘保持滤波算法。此外,它可以根据引导图的变化趋势来约束输入图像,可以解决梯度反转的问题。为了使提取的HFC与MS图像相似,我们使用I作为引导映射,并对图像(P)进行滤波以获得HFC(HP)。
大多数泛锐化方法关注PAN图像的空间结构,但忽略了MS图像中的一些重要空间结构,导致最终结果与参考图像不同。这个问题可以通过融合源图像的高频来解决,以增强注入的高频和MS图像之间的相似性。实际上,源图像是在相同的场景中捕获的,但是在存储信息方面具有不同的重点。因此,源图像的空间信息具有很高的相似性,但同时也存在一定的差异,它们的HFC也具有相同的特征,即HFC的整体结构相似,局部细节存在一定的差异.在此基础上,提出了一种基于HFCs相似性和差异性的融合权值,以较好地保留PAN图像的信息,同时补充MS图像的缺失信息。结构相似性(SSIM)是衡量两幅图像相似性的指标,由平均值、标准差和协方差组成,分别代表亮度、对比度和SSIM。均方根误差(RMSE)可以很好地表达两幅图像之间的差异。因此,我们使用SSIM来衡量HFCs的相似性,并使用RMSE来评估HFCs之间的差异。在计算之前,像素值在0和1之间归一化,使得SSIM和RMSE计算的值在0和1之间。因此,所提出的融合权重定义如下: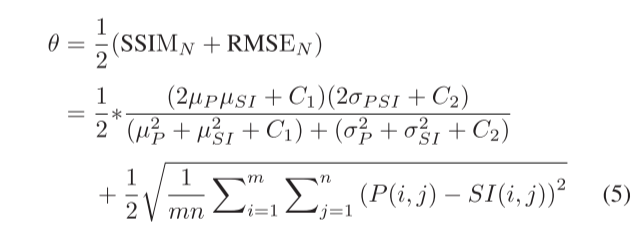
其中SSIMN和RMSEN分别表示归一化的SSIM和RMSE。μP和μSI分别代表P和SI的平均值。σP和σSI分别表示P和SI的方差。σPSI表示P和SI的协方差。C1 =(k1 L)2和C2 =(k2 L)2表示用于保持稳定性的常数,L表示像素值的动态范围。方程(5)可分为两部分:前半部分和后半部分,分别代表HFCs之间的相似性和差异性。为了使融合HFC更好地保留HFCs(HSI)和HP的信息,将θ作为HSI的权重,将(1-θ)作为HP的权重。因此,利用所提出的融合权重,融合策略被定义为: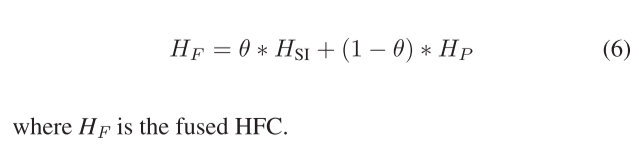
Injection Coefficients Based on the Spatial and Spectral Relationship
在注入模型中,注入系数在将融合后的HFC注入UPMS图像的过程中起着关键作用。良好的注入系数可以提高信息注入的准确性。如果注入系数太大或太小,最终的全息锐化结果会出现空间或频谱失真。因此,寻找合适的注入系数是非常重要的。自适应IHS(AIHS)通过计算源图像的边缘信息来获得注入系数,其可以表示如下:
尽管这种方法是基于空间信息的,但它忽略了质谱图像光谱之间的关系。因此,空间信息的注入可能导致MS图像的光谱之间的原始比率的变化。解决这一问题的一个实际方法是利用光谱信息来约束注入系数。因此,在本文中,我们提出了联合收割机的空间和光谱信息来设计更好的注入系数。在AIHS的基础上,通过考虑PAN图像与MS图像各个光谱波段之间的关系,提出了一种光谱信息约束来优化注入系数。因此,PAN图像和MS图像的每个光谱带的SSIM乘以PAN图像和MS图像的每个光谱带的标准偏差的比率,其被设计为
随后,谱关系Wos k被用来约束gE k以获得谱约束系数。然后将gE k和频谱约束系数组合以获得最终注入系数gk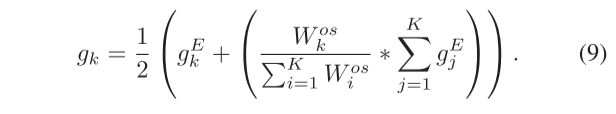
最后,通过注入系数gk将融合高频(HF)注入到~ Mk中,并且因此通过下式获得泛锐化结果(^Mk):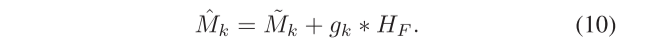
这篇关于【基于MRA:自适应高频融合和注入系数优化:Pansharpening】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




