【路径规划】基于matlab JAYA算法栅格地图机器人最短路径规划【含Matlab源码 2851期】

本文主要是介绍【路径规划】基于matlab JAYA算法栅格地图机器人最短路径规划【含Matlab源码 2851期】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

✅博主简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，Matlab项目合作可私信。
🍎个人主页：海神之光
🏆代码获取方式：
海神之光Matlab王者学习之路—代码获取方式
⛳️座右铭：行百里者，半于九十。

更多Matlab仿真内容点击👇
Matlab图像处理（进阶版）
路径规划（Matlab）
神经网络预测与分类（Matlab）
优化求解（Matlab）
语音处理（Matlab）
信号处理（Matlab）
车间调度（Matlab）

⛄一、JAYA算法及栅格地图简介

1 JAYA算法
Jaya算法是一种基于种群的优化算法，用于解决连续优化问题。它的全称是 “Jaya Algorithm”，其中 “Jaya” 代表了两个开发者的名字，分别为 Dr. R. V. Rao 和 Dr. V. Pandu Ranga。

Jaya算法的思想很简单，它通过不断迭代更新种群中的个体解来寻找最优解。在每一次迭代中，Jaya算法会根据目标函数的值来调整个体解的位置。具体而言，它通过比较当前个体解和邻近个体解的值来更新个体解，从而使得目标函数的值不断减小。

Jaya算法的优势在于其简单性和易于实现性。它不需要设置复杂的参数，也不需要求解梯度等信息，因此在一些实际问题中具有较好的应用效果。然而，Jaya算法也有其局限性，例如在处理高维问题和非凸问题时可能会遇到困难。

对于栅格地图上的机器人最短路径规划问题，Jaya算法可以被用作一种优化算法来寻找最短路径。这种问题可以被抽象为一个在栅格地图上的路径搜索问题，其中机器人需要从起点到达目标点，并且希望路径长度最短。

首先，将栅格地图表示为一个二维数组，其中每个元素代表一个栅格点的状态（例如，可通行或障碍物）。然后，可以使用Jaya算法来搜索最短路径。

在Jaya算法中，种群中的个体解可以表示为机器人在栅格地图上的路径。每个个体解由一系列坐标点组成，表示机器人的移动路径。在每一次迭代中，通过比较个体解的路径长度来更新个体解，使得路径长度逐渐减小。

具体而言，可以使用启发式算法（如A*算法）来计算个体解的路径长度。在每一次迭代中，根据目标函数（即路径长度）的值，使用Jaya算法来调整个体解的位置。通过不断迭代和更新个体解，最终可以找到一条最短路径。

2 栅格地图
2.1 栅格法应用背景
路径规划时首先要获取环境信息，建立环境地图，合理的环境表示有利于建立规划方法和选择合适的搜索算法，最终实现较少的时间开销而规划出较为满意的路径。一般使用栅格法在静态环境下建立环境地图。
2.2 栅格法实质
将AGV的工作环境进行单元分割，将其用大小相等的方块表示出来，这样栅格大小的选取是影响规划算法性能的一个很重要的因素。栅格较小的话，由栅格地图所表示的环境信息将会非常清晰，但由于需要存储较多的信息，会增大存储开销，同时干扰信号也会随之增加，规划速度会相应降低，实时性得不到保证；反之，由于信息存储量少，抗干扰能力有所增强，规划速随之增快，但环境信息划分会变得较为模糊，不利于有效路径的规划。在描述环境信息时障碍物所在区域在栅格地图中呈现为黑色，地图矩阵中标为1，可自由通行区域在栅格地图中呈现为白色，地图矩阵中标为0。路径规划的目的就是在建立好的环境地图中找到一条最优的可通行路径，所以使用栅格法建立环境地图时，栅格大小的合理设定非常关键。
2.3 10乘10的静态环境地图
在这里插入图片描述
10乘10的静态环境地图代码

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%建立环境地图%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function DrawMap(map)
n = size(map);
step = 1;
a = 0 : step :n(1);
b = 0 : step :n(2);
figure(1)
axis([0 n(2) 0 n(1)]); %设置地图横纵尺寸
set(gca,'xtick',b,'ytick',a,'GridLineStyle','-',...
'xGrid','on','yGrid','on');
hold on
r = 1;
for(i=1:n(1))         %设置障碍物的左下角点的x,y坐标for(j=1:n(2))if(map(i,j)==1)p(r,1)=j-1;p(r,2)=i-1;fill([p(r,1) p(r,1) + step p(r,1) + step p(r,1)],...[p(r,2) p(r,2) p(r,2) + step p(r,2) + step ],'k');r=r+1;hold onendend
end%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%栅格数字标识%%%%%%%%%%%%%%%%%%%%%%%%%%%%
x_text = 1:1:n(1)*n(2); %产生所需数值.
for i = 1:1:n(1)*n(2)[row,col] = ind2sub([n(2),n(1)],i);text(row-0.9,col-0.5,num2str(x_text(i)),'FontSize',8,'Color','0.7 0.7 0.7');
end
hold on
axis square

建立环境矩阵，1代表黑色栅格，0代表白色栅格，调用以上程序，即可得到上述环境地图。

map=[0 0 0 1 0 0 1 0 0 0;1 0 0 0 0 1 1 0 0 0;0 0 1 0 0 0 1 1 0 0;0 0 0 0 0 0 0 0 0 0;0 0 0 0 0 1 0 0 1 0;1 0 0 0 0 1 1 0 0 0;0 0 0 1 0 0 0 0 0 0;1 1 1 0 0 0 1 0 0 0;0 0 0 0 0 1 1 0 0 0;0 0 0 0 0 1 1 0 0 0;];DrawMap(map);         %得到环境地图

2.4 栅格地图中障碍栅格处路径约束
移动体栅格环境中多采用八方向的移动方式，此移动方式在完全可通行区域不存在运行安全问题，当
移动体周围存在障碍栅格时此移动方式可能会发生与障碍物栅格的碰撞问题，为解决此问题加入约束
条件，当在分别与障碍物栅格水平方向和垂直方向的可行栅格两栅格之间通行时，禁止移动体采用对
角式移动方式。
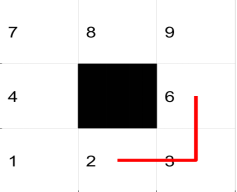
在这里插入图片描述

约束条件的加入，实质是改变栅格地图的邻接矩阵，将障碍栅格(数字为“1”的矩阵元素)的对角栅格
设为不可达，即将对角栅格的距离值改为无穷大。其实现MATLAB代码如下：
代码：

%约束移动体在障碍栅格对角运动
%通过优化邻接矩阵实现
%%%%%%%%%%%%%%%%%% 约束移动体移动方式 %%%%%%%%%%%%%%%%%
function W=OPW(map,W)
% map 地图矩阵  % W 邻接矩阵
n = size(map);
num = n(1)*n(2);
for(j=1:n(1))for(z=1:n(2))if(map(j,z)==1)if(j==1)                  %若障碍物在第一行if(z==1)               %若障碍物为第一行的第一个W(j+1,j+n(2)*j)=Inf;W(j+n(2)*j,j+1)=Inf;elseif(z==n(2))         %若障碍物为第一行的最后一个W(n(2)-1,n(2)+n(1)*j)=Inf;W(n(2)+n(1)*j,n(2)-1)=Inf;else                %若障碍物为第一行的其他W(z-1,z+j*n(2))=Inf;W(z+j*n(2),z-1)=Inf;W(z+1,z+j*n(2))=Inf;W(z+j*n(2),z+1)=Inf;endendendif(j==n(1))               %若障碍物在最后一行if(z==1)               %若障碍物为最后一行的第一个W(z+n(2)*(j-2),z+n(2)*(j-1)+1)=Inf;W(z+n(2)*(j-1)+1,z+n(2)*(j-2))=Inf;elseif(z==n(2))            %若障碍物为最后一行的最后一个W(n(1)*n(2)-1,(n(1)-1)*n(2))=Inf;W((n(1)-1)*n(2),n(1)*n(2)-1)=Inf;else                   %若障碍物为最后一行的其他W((j-2)*n(2)+z,(j-1)*n(2)+z-1)=Inf;W((j-1)*n(2)+z-1,(j-2)*n(2)+z)=Inf;W((j-2)*n(2)+z,(j-1)*n(2)+z+1)=Inf;W((j-1)*n(2)+z+1,(j-2)*n(2)+z)=Inf;endendendif(z==1)              if(j~=1&&j~=n(1))       %若障碍物在第一列非边缘位置 W(z+(j-2)*n(2),z+1+(j-1)*n(2))=Inf;W(z+1+(j-1)*n(2),z+(j-2)*n(2))=Inf;W(z+1+(j-1)*n(2),z+j*n(2))=Inf;W(z+j*n(2),z+1+(j-1)*n(2))=Inf;endendif(z==n(2))if(j~=1&&j~=n(1))         %若障碍物在最后一列非边缘位置 W((j+1)*n(2),j*n(2)-1)=Inf;W(j*n(2)-1,(j+1)*n(2))=Inf;W(j*n(2)-1,(j-1)*n(2))=Inf;W((j-1)*n(2),j*n(2)-1)=Inf;endendif(j~=1&&j~=n(1)&&z~=1&&z~=n(2))   %若障碍物在非边缘位置W(z+(j-1)*n(2)-1,z+j*n(2))=Inf;W(z+j*n(2),z+(j-1)*n(2)-1)=Inf;W(z+j*n(2),z+(j-1)*n(2)+1)=Inf;W(z+(j-1)*n(2)+1,z+j*n(2))=Inf;W(z+(j-1)*n(2)-1,z+(j-2)*n(2))=Inf;W(z+(j-2)*n(2),z+(j-1)*n(2)-1)=Inf;W(z+(j-2)*n(2),z+(j-1)*n(2)+1)=Inf;W(z+(j-1)*n(2)+1,z+(j-2)*n(2))=Inf;endendendend
end

2.5 栅格法案例
下面以Djkstra算法为例，其实现如下：

map=[0 0 0 1 0 0 1 0 0 0;1 0 0 0 0 1 1 0 0 0;0 0 1 0 0 0 1 1 0 0;0 0 0 0 0 0 0 0 0 0;0 0 0 0 0 1 0 0 1 0;1 0 0 0 0 1 1 0 0 0;0 0 0 1 0 0 0 0 0 0;1 1 1 0 0 0 1 0 0 0;0 0 0 0 0 1 1 0 0 0;0 0 0 0 0 1 1 0 0 0;];%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%建立环境矩阵map%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
DrawMap(map); %得到环境地图
W=G2D(map);   %得到环境地图的邻接矩阵
W(W==0)=Inf;  %邻接矩阵数值处理
W=OPW(map,W); %优化邻接矩阵
[distance,path]=dijkstra(W,1,100);%设置起始栅格，得到最短路径距离以及栅格路径
[x,y]=Get_xy(distance,path,map);   %得到栅格相应的x，y坐标
Plot(distance,x,y);   %画出路径

运行结果如下：
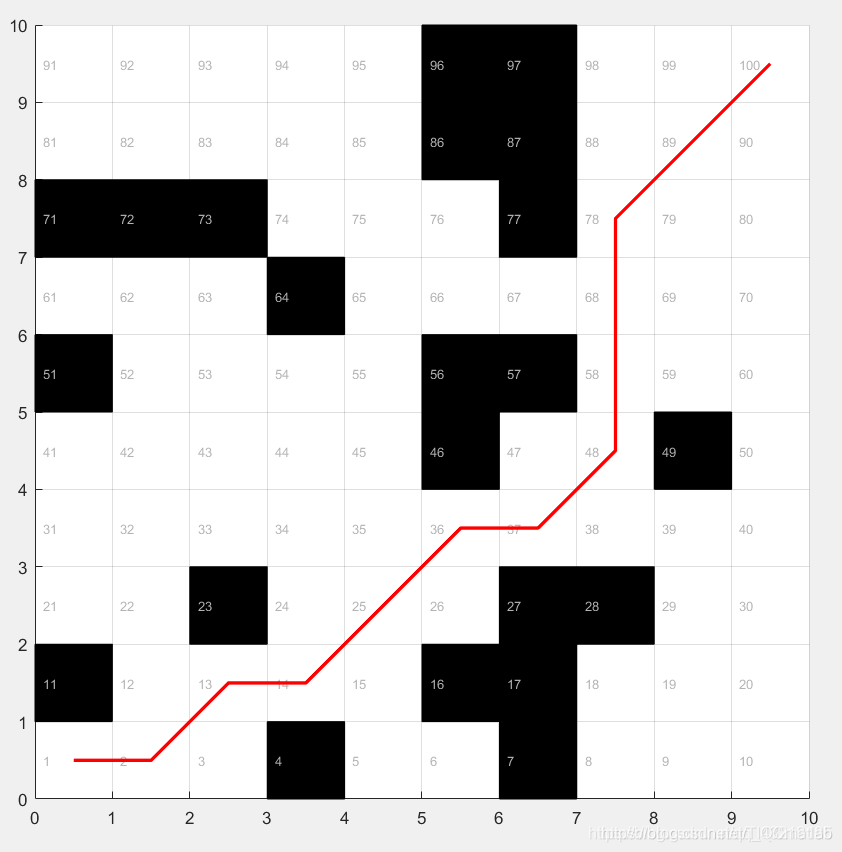
在这里插入图片描述
其中函数程序：
DrawMap(map) 详见建立栅格地图
W=G2D(map) ；详见建立邻接矩阵
[distance， path] =dijkstra(W， 1， 100) 详见Djk stra算法
[x， y] =Get_xy(distance， path， map) ；
Plot(distance， x， y) ；

⛄二、部分源代码

clc
clear
close all
tic
%% 地图
G=[0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
0 1 1 1 0 0 1 1 1 0 1 1 1 1 0 0 0 0 0 0;
0 1 1 1 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0;
0 0 0 0 1 1 0 1 1 0 1 1 1 1 0 0 0 0 0 0;
0 0 0 0 1 0 0 1 1 0 1 1 1 1 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 1 1 1 0;
0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 1 1 1 0;
1 1 1 1 0 0 0 0 0 0 0 0 1 1 0 1 1 1 1 0;
1 1 1 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 1 1 0 1 1 1 0 0 0 0 0 1 1 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0;
0 0 1 1 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0;];
for i=1:20/2
for j=1:20
m=G(i,j);
n=G(21-i,j);
G(i,j)=n;
G(21-i,j)=m;
end
end
%%
S = [1 1];
E = [20 20];
G0 = G;
G = G0(S(1):E(1),S(2):E(2));
[Xmax,dimensions] = size(G);
dimensions = dimensions - 2;
X_min = 1;
%% 参数设置
max_gen = 200; % 最大迭代次数
num_polution = 50; % 种群数量
fboj=@(x)fitness(x,G,X_min,Xmax);
[fit_global_best,global_best,final_goal]=CLJAYA(num_polution,max_gen, X_min,Xmax,dimensions,fboj);
toc
%% 结果分析
global_best1 = round(global_best);
fit_global_best
figure(1)
plot(final_goal,‘b-’);
xlabel(‘迭代次数’)
ylabel(‘适应度值’)
title(‘JAYA优化迭代曲线’)
route = [S(1) global_best1 E(1)];
path=generateContinuousRoute(route,G);
% path=shortenRoute(path);
path=GenerateSmoothPath(path,G);
path=GenerateSmoothPath(path,G);
figure(2)
for i=1:20/2
for j=1:20
m=G(i,j);
n=G(21-i,j);
G(i,j)=n;
G(21-i,j)=m;
end
end
n=20;
for i=1:20
for j=1:20
if G(i,j)==1
x1=j-1;y1=n-i;
x2=j;y2=n-i;
x3=j;y3=n-i+1;
x4=j-1;y4=n-i+1;
fill([x1,x2,x3,x4],[y1,y2,y3,y4],‘r’);
hold on
else
x1=j-1;y1=n-i;
x2=j;y2=n-i;
x3=j;y3=n-i+1;
x4=j-1;y4=n-i+1;
fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]);
hold on
end
end
end
hold on
xlabel(‘Environment 1’)
drawPath(path,G)
title(‘基于JAYA优化算法实现栅格地图机器人路径规划’)

⛄三、运行结果

在这里插入图片描述

⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]马云涛, 吕恒, 牛金星. 基于Jaya算法的机器人路径规划研究[J]. 计算机科学与探索, 2016, 10(8): 1117-1127.
[2]邹春雷, 胥满芳. 基于Jaya算法的栅格地图机器人路径规划方法[J]. 计算机工程与设计, 2019, 40(2): 601-606.
[3]张晓东, 郭鹏, 赵华玉. 基于Jaya算法的栅格地图机器人路径规划研究[J]. 计算机应用与软件, 2018, 35(6): 204-207

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除

🍅 仿真咨询
1 各类智能优化算法改进及应用
生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化

2 机器学习和深度学习方面
卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

3 图像处理方面
图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

4 路径规划方面
旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化

5 无人机应用方面
无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配

6 无线传感器定位及布局方面
传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

7 信号处理方面
信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

8 电力系统方面
微电网优化、无功优化、配电网重构、储能配置

9 元胞自动机方面
交通流人群疏散病毒扩散晶体生长

10 雷达方面
卡尔曼滤波跟踪、航迹关联、航迹融合

这篇关于【路径规划】基于matlab JAYA算法栅格地图机器人最短路径规划【含Matlab源码 2851期】的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！