川川数模-D3-非线性规划（1）

本文主要是介绍川川数模-D3-非线性规划（1），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

非线性规划数学模型

非线性规划函数

x = fmincon(fun,x0,A,b) 从 x0 开始，尝试在满足线性不等式 A*x ≤ b 的情况下寻找 fun 中所述的函数的最小值点 x。x0 可以是标量、向量或矩阵。
x = fmincon(fun,x0,A,b,Aeq,beq) 在满足线性等式 Aeq*x = beq 以及不等式 A*x ≤ b 的情况下最小化 fun。如果不存在不等式，则设置 A = [] 和 b = []。
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub) 对 x 中的设计变量定义一组下界和上界，使解始终在 lb ≤ x ≤ ub 范围内。如果不存在等式，请设置 Aeq = [] 和 beq = []。如果 x(i) 无下界，请设置 lb(i) = -Inf，如果 x(i) 无上界，请设置 ub(i) = Inf。
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options) 使用 options 所指定的优化选项执行最小化。使用 optimoptions 可设置这些选项。如果没有非线性不等式或等式约束，请设置 nonlcon = []。
%（非线性会用nonlcon）

题目1

线性条件约束

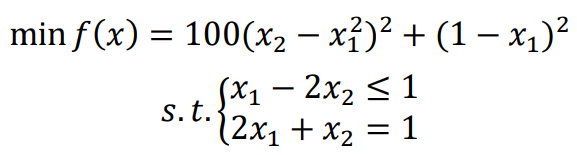
实验说明及源代码

clc
clear all
fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;x0 = [1,1];%初始点设置自行不同
A = [1,-2];
b = 1;
Aeq = [2,1];
beq = 1;
[x,y] = fmincon(fun,x0,A,b,Aeq,beq)

实验结果

x =0.4149    0.1701
y =0.3427

题目2
非线性条件约束
min f (x) = x₁² + x₂² + x₃² + 8
x₁² − x₂ + x₃ ² ≥ 0
x₁ + x₂² + x₃ ³ ≤ 20
−x₁ − x₂² + 2 = 0
x₂ + 2x₃² = 3
x₁,x₂,x₃ ≥ 0

实验说明及源代码

clc
clear all
fun1=@(x)sum(x.^2)+8;
[x,y] = fmincon(fun1,rand(3,1),[],[],[],[],zeros(3,1),[], @fun2)function [c,ceq]=fun2(x)
c=[-x(1)^2+x(2)-x(3)^2x(1)+x(2)^2+x(3)^3-20];  %非线性不等式约束
ceq=[-x(1)-x(2)^2+2x(2)+2*x(3)^2-3]; %非线性等式约束
end