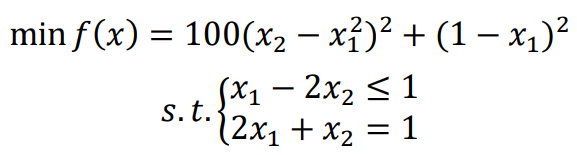川川专题
川川本人著作《Python3编程从零基础到实战》
在数字时代,Python已经成为了一种极为强大和灵活的编程语言,它的应用范围从网站开发到数据科学,再到机器学习和人工智能。无论你是一名编程新手还是希望深化已有技能的开发者,《Python3编程从零基础到实战》将成为你通往Python世界的金钥匙。这本书以其全面的内容、实战案例和深入浅出的教学风格,保证让你在Python的旅程中游刃有余。 文章目录 开启Python旅程掌握核心概念应用于
川川数模-D2-整数规划(1)
题目1 (暂时忽略限制条件为整数求解) 实验说明及源代码 >> c=[40,90];>> a=[9,7;7,20];b=[56;70];>> aeq=[];beq=[];>> lb=[0;0];ub=[inf;inf];>> [x,fval]=linprog(-c,a,b,aeq,beq,lb,ub) 实验结果 Optimal solution found.x =4.809
跟着川川打卡爬虫第一天
基本上没啥问题就是自己比较傻,然后就没了,应该是成功了吧。 首先是去网站下载 直接从川川那复制链接,然后去网站下载,等待下载完成。没有什么特殊的地方。 下载完就是安装了 跟着川川的进度,安装没啥问题。安装完后卡住了,我不知道咋打开命令行窗口,百度了一下(没想到吧,居然还有人不会命令窗口。 然后是汉化,川川说看自己个人,然后说以后是英语,我就没汉化了。主要还是不知道咋打开像川川那
打卡川川的线性规划matlab题目
题目 目录 题目 clc clear all %matlab默认求线性规划时,以下限为标准进行求解所以遇上小于等于需要变化c=[2 3 -5] %目标函数a=[-2,5,-1;1,3,1] %左边约束b=[-10;12] %右边约束aeq=[1,1,1] %无等式可置零beq=7
跟着川川学习爬虫的第一天
一、anaconda安装 官网下载: 选择自己电脑合适的下载 然后进行安装 然后我们就得到了它,哈哈哈 二、jupyter安装配置 右键,管理员运行后: 点击后自动跳转jupyter,但是这里我出现了问题,并没有自动跳转 在川川大佬的帮助下,重置了电脑用户名,终于跳转了,哈哈哈,贼开心 三、jupyter汉化 还是想着慢慢适应英文,
川川数模-D4-多元线性回归模型
一元线性回归 1.根据数据画图; 2.根据所画图形进行分析,调整模型; eg: 源代码1 clear allclcx=1:10;y=[2650,1942,1493,1086,766,539,485,291,224,202];z=zeros(size(y));N=length(y);for i =1:Nz(i)=log(y(i));%调整plot(x(i),z(i),'ok');ho
川川数模-D1-线性规划(1)
题目 1.题目思路 matlab求解线性规划标准形式: 2.实验说明及源代码 >> c=[2,3,-5];>> aeq=[1,1,1];beq=7;>> a=[-2,5,-1;1,3,1];b=[-10;12];>> lb=[0;0;0];ub=[inf;inf;inf];>> [x,fval]=linprog(-c,a,b,aeq,beq,lb,ub);%-c是因为要求最
川川数模训练营打卡第二天-整数规划(1)
例题: 一.如果我们用线性规划做: 代码: clc clear all c=[40 90]; a=[9 7;7 20]; b=[56;70]; aeq=[ ]; beq=[ ]; Ib=[0;0]; ub=[inf;inf]; [x,fval]=linprog(-c,a,b,aeq,beq,Ib,ub); x%获得对应的x1,x2 best=c*x 代码如图
川川数模训练营第一天打卡-线性规划
问题:求解该线性规划对应的最大值z以及x1,x2,x3. 一.代码过程 clc clear all c=[2,3,-5];%目标函数的系数确定 a=[-2,5,-1;1,3,1];%约束条件左边约束 b=[-10;12];%约束条件右边约束 aeq=[1,1,1];%等式左边约束(即等式左边的系数) beq=7;%等式右边约束(即等式右边的数) Ib=[0;0;0];%下限
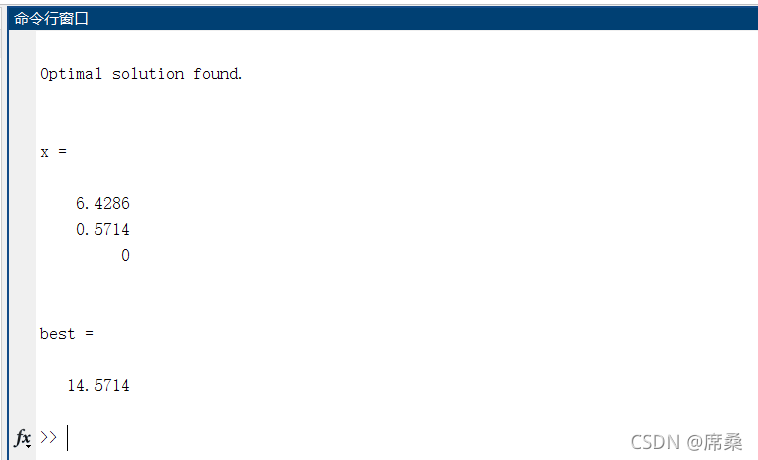
川川数模-D3-非线性规划(1)
非线性规划数学模型 非线性规划函数 x = fmincon(fun,x0,A,b) 从 x0 开始,尝试在满足线性不等式 A*x ≤ b 的情况下寻找 fun 中所述的函数的最小值点 x。x0 可以是标量、向量或矩阵。x = fmincon(fun,x0,A,b,Aeq,beq) 在满足线性等式 Aeq*x = beq 以及不等式 A*x ≤ b 的情况下最小化 fun。如果不存在不等式,则