川川数模-D4-多元线性回归模型

一元线性回归

1.根据数据画图；
2.根据所画图形进行分析，调整模型；
eg:
源代码1

clear all
clc
x=1:10;
y=[2650,1942,1493,1086,766,539,485,291,224,202];
z=zeros(size(y));
N=length(y);
for i =1:Nz(i)=log(y(i));%调整plot(x(i),z(i),'ok');hold on
end

实验结果1

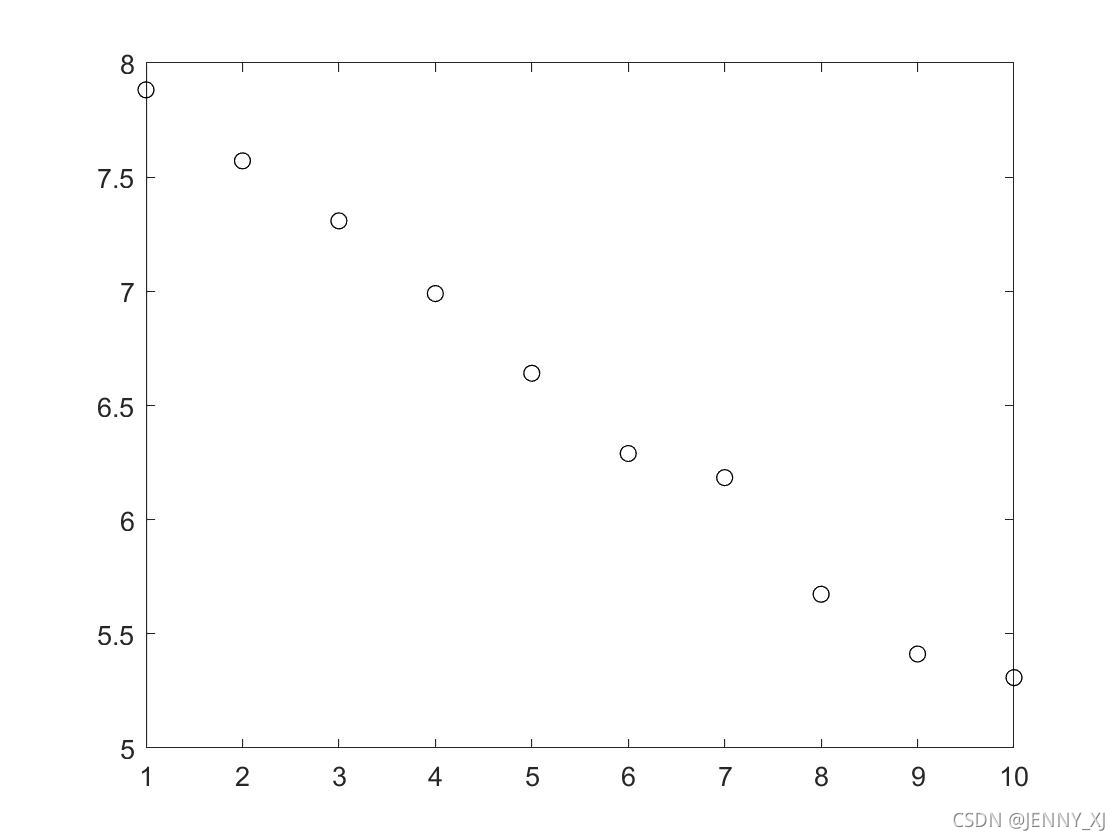
源代码2

clear all
clc
x=1:10;
y=[2650,1942,1493,1086,766,539,485,291,224,202];
z=zeros(size(y));
N=length(y);
for i =1:Nz(i)=log(y(i));
end
[p,s]=polyfit(x,z,1)
y1=polyval(p,x);
hold on
plot(x,y1)

实验结果2

p =-0.2984    8.1671s = 包含以下字段的 struct:R: [2×2 double]df: 8normr: 0.2316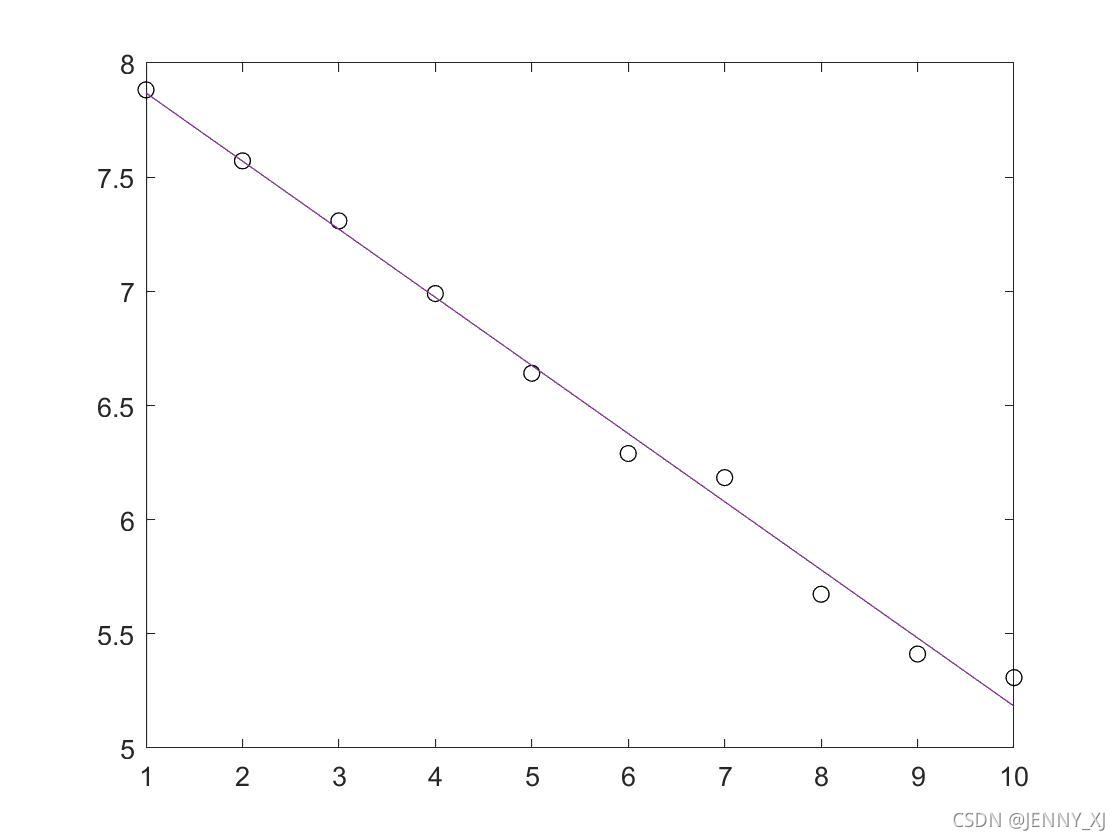

p = polyfit(x,y,n); % 其中x,y表示需要拟合的坐标点，大小需要一样； n表示多项式拟合的次数。 %
返回值p表示多项式拟合的系数，系数从高到低排列

polyfit使用方法

多元线性回归

[b,bint,r,rint,stats]=regress(y,x，alpha)
alpha为显著性水平，缺省设定为0.05，b表示为输出输出量，bint为回归系数估计值和它们的置信区间，r为残差，rint为置信区间，stats适用于检验回归模型的统计量。
regress用法

例题：


实验分析及源代码：

clear all
clc
y=[90.9,97.4,113.5,125.7,122.8,133.3,149.3,144.2,166.4,195.0,229.8,228.7,206.1,257.9,324.1,386.6,423.0,401.9,474.9,424.5]
x1=[596.7,637.7,691.1,756,799,873.4,944,992.7,1077.6,1185.9,1326.4,1434.2,1549.2,1718,1918.3,2163.9,2417.8,2631.7,2954.7,3073]
x2=[0.7167,0.7277,0.7436,0.7676,0.7906,0.8254,0.8679,0.9145,0.9601,1,1.0575,1.1508,1.2579,1.3234,1.4005,1.5042,1.6342,1.7842,1.9514,2.0688]
y=[y'];
x=[ones(size(x1')),x1',x2'];
[b,bint,r,rint,stats]=regress(y,x)

实验结果

b =322.72500.6185-859.4790bint =1.0e+03 *0.2243    0.42110.0005    0.0008-1.1215   -0.5975r =15.13065.72812.4682-4.8421-14.5677-20.1710-11.3062-6.47332.4119-1.6737-4.34688.07296.400610.101018.690018.42509.5311-14.93492.0085-20.6521rint =-8.8991   39.1602-20.0842   31.5404-23.8131   28.7495-30.9710   21.2868-39.7357   10.6002-44.1322    3.7901-37.1412   14.5288-32.9501   20.0034-24.3505   29.1743-28.4886   25.1412-30.1760   21.4823-18.6017   34.7476-16.4416   29.2428-15.3656   35.5677-6.2548   43.6348-4.6295   41.4795-13.7104   32.7727-39.1156    9.2458-22.1655   26.1825-38.3634   -2.9408stats =0.9908  919.8529    0.0000  161.7073

与书本上答案相符

其他
polyfit使用方法
regress用法