本文主要是介绍川川数模训练营打卡第二天-整数规划(1),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
例题:
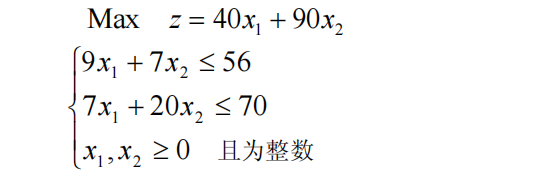
一.如果我们用线性规划做:
代码:
clc
clear all
c=[40 90];
a=[9 7;7 20];
b=[56;70];
aeq=[ ];
beq=[ ];
Ib=[0;0];
ub=[inf;inf];
[x,fval]=linprog(-c,a,b,aeq,beq,Ib,ub);
x%获得对应的x1,x2
best=c*x
代码如图:

执行结果如图:

x1,x2都不是整数,不满足最优解。
二.分支定界法步骤
此方法可以用于解纯整数或混合的整数规划问题。
过程如下:
三.代码编写
问题B1,给x1分支
clc
clear all
c=[40 90]; %用目标函数系数来确定
a=[9 7 ;7 20];%约束条件左边约束
b=[56 70];%约束条件右边系数
aeq=[ ];%没有等式约束,因此aeq,beq都为空
beq=[ ];
lb=[0;0];%下限依然都为0
ub=[4;inf];%x1上限为4,x2没有上限
[x,y]=linprog(-c,a,b,aeq,beq,lb,ub); %这里没有等式约束,对应的矩阵为空矩阵
x%获取对应x1,x2
best=c*x%计算最优值
运行结果如下:

对x1做了分支之后,还要计算x1的另一半
问题B2:
目标函数 Max z = 40x1 + 90x2
条件约束:
9*x1+7*x2<=56
7*x1+20*x2<=70
x1>=5 x2>0
代码如下:
clc
clear all
c=[40 90]; %用目标函数系数来确定
a=[9 7 ;7 20];%约束条件左边约束
b=[56 70];%约束条件右边系数
aeq=[ ];%没有等式约束,因此aeq,beq都为空
beq=[ ];
lb=[5;0];%x1下限为5,x2下限为0
ub=[inf;inf];%x1,x2没有上限
[x,y]=linprog(-c,a,b,aeq,beq,lb,ub); %这里没有等式约束,对应的矩阵为空矩阵
x%获取对应x1,x2
best=c*x%计算最优值
运行结果

接下来给z定界:0<=z<=349
问题B3,给x2分支
目标函数: Max z = 40x1 + 90x2
约束条件:
9*x1+7*x2<=56
7*x1+20*x2<=70
0<=x1<=4 2>x2>0
代码如下:
clc
clear all
c=[40 90];%用目标函数系数来确定
a=[9 7 ;7 20];%约束条件左边约束
b=[56 70];%约束条件右边系数
aeq=[];%没有等式约束,因此aeq,beq都为空
beq=[];
lb=[0;0];%下限依然都为0
ub=[4;2];%x1上限为4,x2上限为2
[x,y]=linprog(-c,a,b,aeq,beq,lb,ub); %这里没有等式约束,对应的矩阵为空矩阵
x %获取对应x1,x2
best=c*x%计算最优值
结果:
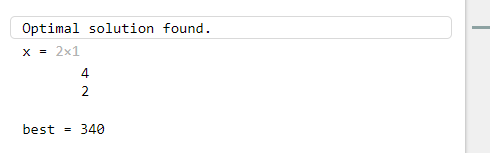
问题B4:
目标函数: Max z = 40x1 + 90x2
条件约束:
9*x1+7*x2<=56
7*x1+20*x2<=70
0<=x1<=4 x2>3
代码同上:
clc
clear all
c=[40 90];%用目标函数系数来确定
a=[9 7 ;7 20];%约束条件左边约束
b=[56 70];%约束条件右边系数
aeq=[];%没有等式约束,因此aeq,beq都为空
beq=[];
lb=[0;3];%x1下限为0,x2下限为3
ub=[4;inf];%x1上限为4,x2无上限
[x,y]=linprog(-c,a,b,aeq,beq,lb,ub); %这里没有等式约束,对应的矩阵为空矩阵
x %获取对应x1,x2
best=c*x%计算最优值
结果如下:

再次确定z 的范围为[340,341]
问题B5:
目标函数: Max z = 40x1 + 90x2
约束条件:
9*x1+7*x2<=56
7*x1+20*x2<=70
x1>=5 1>x2>0
clc
clear all
c=[40 90];%用目标函数系数来确定
a=[9 7 ;7 20];%约束条件左边约束
b=[56 70];%约束条件右边系数
aeq=[];%没有等式约束,因此aeq,beq都为空
beq=[];
lb=[5;0];%x1下限为5,x2下限为0
ub=[inf;1];%x1无上限,x2上限为1
[x,y]=linprog(-c,a,b,aeq,beq,lb,ub);%这里没有等式约束,对应的矩阵为空矩阵
x%获取对应x1,x2
best=c*x%计算最优值
结果如下:

问题B7:
目标函数: Max z = 40x1 + 90x2
约束条件:
9*x1+7*x2<=56
7*x1+20*x2<=70
x1>=5 x2>2
代码:
clc
clear all
c=[40 90];%用目标函数系数来确定
a=[9 7 ;7 20];%约束条件左边约束
b=[56 70];%约束条件右边系数
aeq=[];%没有等式约束,因此aeq,beq都为空
beq=[];
lb=[5;2];%x1下限为5,x2下限为2
ub=[inf;inf];%x1无上限,x2无上限
[x,y]=linprog(-c,a,b,aeq,beq,lb,ub);%这里没有等式约束,对应的矩阵为空矩阵
x%获取对应x1,x2
best=c*x%计算最优值
结果如下:

是无解的意思。
最后取符合条件的:
x1 = 4, x2 = 2,z = 340,即为答案。
三.川川的总结
将要求解的整数规划问题称为问题A,将与它对应的线性规划问题称为B.
1.B没有可行解,这时A也没有可行解,则停止。
2.B有最优解,并符合问题A的整数条件,B的最优解即为A的最优解,则停止。
3.B有最优解,但不符合问题A的整数条件,记它的目标函数值为z,通过上述6个步骤进行分支定界法,剪枝,最后得出结果。
这篇关于川川数模训练营打卡第二天-整数规划(1)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!