【博士每天一篇文献-算法】Gradient Episodic Memory for Continual Learning

本文主要是介绍【博士每天一篇文献-算法】Gradient Episodic Memory for Continual Learning，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

阅读时间：2023-10-26

1 介绍

年份：2017
作者：David Lopez-Paz, Marc’Aurelio Ranzato
期刊：Part of Advances in Neural Information Processing Systems 30 (NIPS 2017)
引用量：2044
针对持续学习中灾难性遗忘问题提出一种名为Gradient Episodic Memory（GEM）算法，这种算法核心思想是将有益的知识传递给过去的任务。还提出了一组评估学习模型在任务间转移知识和避免灾难性遗忘能力的度量指标。

2 创新点

（1）梯度时序记忆（GEM）：GEM模型通过构建一个经验记忆库，将有益的知识传递到过去的任务中，从而减轻了遗忘现象。通过在不同任务之间传递知识，模型能够在面临新任务时保持良好的性能。
（2）评估指标：该论文引入了一组评估指标，用于评估学习模型在持续学习场景下的能力。除了考虑模型的准确性之外，还关注模型的知识传递能力和遗忘情况。通过这些指标，可以更全面地评估模型在持续学习中的表现。
（3）训练协议：与以往的研究不同，该论文的训练协议在于每个任务只提供了有限数量的训练样本，并且任务只观察一次。这种协议更贴近现实中的学习场景，并且能够更好地评估模型的泛化能力和遗忘情况。
任务数量大，但每个任务的训练示例数量少
学习只观察每个任务的示例一次
增加报告测量迁移的绩效和遗忘的指标，作者认为除了观察其跨任务的绩效外，评估转移知识的能力也很重要

3 算法

3.1 评价指标

平均准确度（ACC）是模型在所有任务上的平均测试准确度
负向转移（BWT）是模型在观察任务ti后，在之前任务k上的测试准确度降低了多少
正向转移（FWT）是模型在观察任务ti后，在将来任务k上的测试准确度提高了多少
截屏2023-10-27 上午11.01.15.png
其中 $R_{i,j}$ 是在观察到任务 $t_j$ 的最后一个样本之后，模型在任务 $t_j$ 上的测试分类准确度。 $\overline{b}$ 是随机初始化时每个任务的测试准确度向量.

3.2 算法逻辑

算法本质是将episodic memory添加到当前任务的样本中一起进行训练。

“episodic memory”指的是存储当前任务的数据和标签的Ring Buffer内存，即代码中的self.memory_data和self.memory_labs。在持续学习场景中，网络需要不断地学习新任务并保持对旧任务的知识记忆。而Ring Buffer作为一种常见的记忆存储方式，将最近观察到的一定数量的数据和标签存储在内存中，用于后续网络训练和知识迁移。由于内存是按照先进先出（FIFO）的方式进行更新，因此也被称为“Episodic Memory”，即“记忆片段存储器”。

可以在任务k的memory上定义如下损失函数，公式（1）：
$l(f_{\theta},M_k) = \frac{1}{|M_k|} \sum_{x_i,k,y_i \in M_k} l(f_{\theta}(x_i,k),y_i)$

其中 $f_{\theta}$ 是预测模型， $M_k$ 是episodic memory。但这种方式容易在 $M_k$ 中的样本上过拟合。

作者做了第一个实验。采用论文【 iCaRL: Incremental classifier and representation learning】中的知识蒸馏方法，解决这种过拟合。原理是是利用通过将模型中间层的输出（即类别概率）作为“软目标”（即蒸馏目标，soft label）来约束网络的输出，在 $M_k$ 中同时保留其“soft label”。新的损失函数为，公式（2）：

$l(f_{\theta},M_k) =\frac{1}{M_k}(1-\lambda) \times l(f_\theta(x_i,k),y_i)+\lambda \times l(f_{\theta}(x_i,k),y_{soft})$
但是，这种方法这不能正向传输。因此，作者提出了本文的GEM算法。
它并不直接以上的优化公式（1），而是用公式（1）作为线性规划问题的中的一个不等式约束，让其只减不增。定义的目标函数和约束如下公式（3）：

$\quad l(f_{\theta}(x,t),y)\\ l(f_{\theta},M_k) \leq l(f_{\theta}^{t-1},M_k),k<t$

其中 $f_{\theta}^{t-1}$ 是上一个任务学习之后的预测模型。
作者进一步观察到，不需要存储旧的模型 $f_{\theta}^{t-1}$ ，只要确保在每次参数g更新之后，先前任务的损失不会增加即可。这可以通过计算它们的损失梯度向量与建议的更新之间的角度来诊断先前任务损失的增加来确定，用公式（4）表示为：
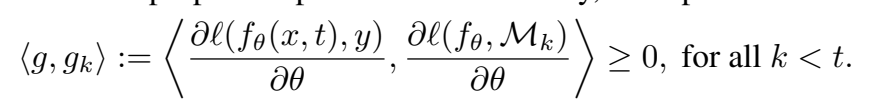
截屏2023-10-27 下午12.16.34.png
如果他们的夹角为锐角，则学习当前任务时，任务k的性能就不会增加。如果出现锐角，将建议的梯度g投影到最接近的满足所有约束公式（4）的梯度 $\widetilde{g}$ （以平方2范数计算）。这样就得到如下优化目标，公式（5）：
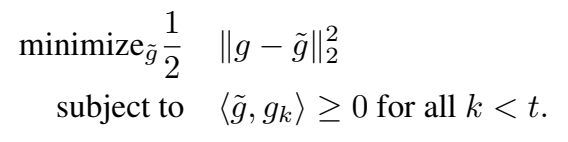
截屏2023-10-27 下午12.23.19.png
这是一个二次规划问题，作者在这里将其转换成其对偶形式进行求解。求解过程如下：
将GEM QP公式（5）写成原始形式，公式（6）：
$\min_{g,z} \frac{1}{2}z^Tz - g^Tz+ \frac{1}{2}g^Tg \\ \text{subject to } Gz \geq 0$
其中 $-(g_1, \ldots, g_{t-1})$ ，且去掉了常数项 $g^Tg$ 。这是一个关于变量z（神经网络的参数个数，可能为百万级）的二次规划问题。因此，可以将GEM QP的对偶形式写成，公式（7）：
$\min_{v} \frac{1}{2}v^TGG^Tv + g^TG^Tv \\ \text{subject to } v \geq 0$
其中 $u = G^Tv + g$ ，常数项 $g^Tg$ 。这是一个关于变量v（迄今为止观察到的任务数量）的二次规划问题。一旦解决了对偶问题找到 $v^{*}$ 后，就可以恢复出梯度投影更新 $\widetilde{g} = G^Tv^{*}+ g$ 。实践中，作者发现将一个小常数 $\gamma \geq 0$ 添加到 $v^*$ 可以使梯度投影更倾向于有益的反向传递更新。

3.3 实现步骤

初始化网络结构和参数：包括输入和输出的维度，网络层数和隐藏单元数，优化算法等。
分配任务内存和梯度内存：为每个任务分配存储当前任务数据和标签的内存，并分配临时的梯度内存用于存储梯度信息。
前向传播：根据当前任务t的输入数据x，通过网络计算输出结果output。
输出调整：如果是CIFAR数据集，则将输出结果调整为预测当前任务的类别。
观察并更新内存：将当前任务的观察数据x和标签y存储到内存中，并更新指针mem_cnt。
计算过去任务的梯度：对于已经观察过的任务，遍历每个任务进行前向传播和反向传播，计算梯度，并存储到梯度内存中。
计算当前任务的梯度：对于当前任务t的数据x和标签y，进行前向传播和反向传播，计算梯度。
检查梯度约束：如果已经观察了多个任务，则检查当前任务的梯度是否违反了约束条件。如果违反了，使用投影算法进行调整。
更新参数：使用优化器根据计算得到的梯度更新网络参数。

5 实验结果分析

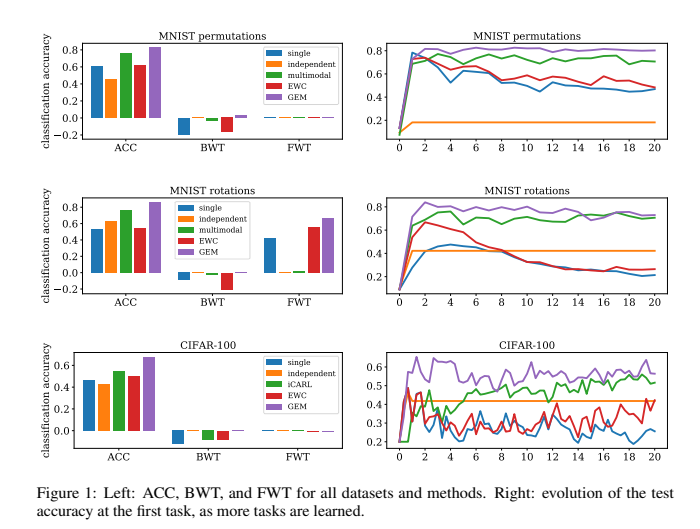
GEM的表现要明显优于像EWC这样的其他持续学习方法，同时计算成本更低（表1）。GEM的高效性来自于优化任务数（实验中为T=20）相等数量的变量，而不是优化参数数量（例如CIFAR100的p=1109240个变量）。GEM的瓶颈是需要在每个学习迭代中计算先前任务的梯度。

6 思考

（1）以上公式（4）损失梯度向量与建议的更新之间的角度的公式没有明白，作者如何观察出来的？如何求解这个角度？
（2）以上公式（7）没有看明白，怎么求解
（3）代码没有看明白，怎么和算法结合起来的
（4）还需要看这篇论文【iCaRL: Incremental classifier and representation learning】

7 代码

https://github.com/facebookresearch/GradientEpisodicMemory/blob/master/model/gem.py

import torch
import torch.nn as nn
import torch.optim as optimimport numpy as np
import quadprogfrom .common import MLP, ResNet18# Auxiliary functions useful for GEM's inner optimization.
# 用于计算CIFAR数据集中每个任务对应的输出偏移量（根据任务数和每个任务对应的分类数），以确定选择哪些输出值。
def compute_offsets(task, nc_per_task, is_cifar):"""Compute offsets for cifar to determine whichoutputs to select for a given task."""if is_cifar:offset1 = task * nc_per_taskoffset2 = (task + 1) * nc_per_taskelse:offset1 = 0offset2 = nc_per_taskreturn offset1, offset2# 用于存储之前训练任务的参数和梯度
def store_grad(pp, grads, grad_dims, tid):"""This stores parameter gradients of past tasks.pp: parametersgrads: gradientsgrad_dims: list with number of parameters per layerstid: task id"""# store the gradientsgrads[:, tid].fill_(0.0)cnt = 0for param in pp():if param.grad is not None:beg = 0 if cnt == 0 else sum(grad_dims[:cnt])en = sum(grad_dims[:cnt + 1])grads[beg: en, tid].copy_(param.grad.data.view(-1))cnt += 1# 用于重写梯度，以解决GEM算法中的违规问题
def overwrite_grad(pp, newgrad, grad_dims):"""This is used to overwrite the gradients with a new gradientvector, whenever violations occur.pp: parametersnewgrad: corrected gradientgrad_dims: list storing number of parameters at each layer"""cnt = 0for param in pp():if param.grad is not None:beg = 0 if cnt == 0 else sum(grad_dims[:cnt])en = sum(grad_dims[:cnt + 1])this_grad = newgrad[beg: en].contiguous().view(param.grad.data.size())param.grad.data.copy_(this_grad)cnt += 1# 用于计算GEM中的二次规划问题的解，以确保当前任务的梯度不会影响旧任务的决策边界设置。
def project2cone2(gradient, memories, margin=0.5, eps=1e-3):"""Solves the GEM dual QP described in the paper given a proposedgradient "gradient", and a memory of task gradients "memories".Overwrites "gradient" with the final projected update.input:  gradient, p-vectorinput:  memories, (t * p)-vectoroutput: x, p-vector"""memories_np = memories.cpu().t().double().numpy()gradient_np = gradient.cpu().contiguous().view(-1).double().numpy()t = memories_np.shape[0]P = np.dot(memories_np, memories_np.transpose())P = 0.5 * (P + P.transpose()) + np.eye(t) * epsq = np.dot(memories_np, gradient_np) * -1G = np.eye(t)h = np.zeros(t) + marginv = quadprog.solve_qp(P, q, G, h)[0]x = np.dot(v, memories_np) + gradient_npgradient.copy_(torch.Tensor(x).view(-1, 1))class Net(nn.Module):def __init__(self,n_inputs,n_outputs,n_tasks,args):super(Net, self).__init__()nl, nh = args.n_layers, args.n_hiddens# GEM算法中用于更新梯度的截断边界self.margin = args.memory_strengthself.is_cifar = (args.data_file == 'cifar100.pt')if self.is_cifar:self.net = ResNet18(n_outputs)else:self.net = MLP([n_inputs] + [nh] * nl + [n_outputs])self.ce = nn.CrossEntropyLoss()self.n_outputs = n_outputs# 优化算法，用于对参数进行优化（此处使用SGD）self.opt = optim.SGD(self.parameters(), args.lr)self.n_memories = args.n_memoriesself.gpu = args.cuda# allocate episodic memory 用于存储当前任务的数据和标签self.memory_data = torch.FloatTensor(n_tasks, self.n_memories, n_inputs)self.memory_labs = torch.LongTensor(n_tasks, self.n_memories)if args.cuda:self.memory_data = self.memory_data.cuda()self.memory_labs = self.memory_labs.cuda()# allocate temporary synaptic memoryself.grad_dims = []for param in self.parameters():self.grad_dims.append(param.data.numel())# 用于存储梯度信息self.grads = torch.Tensor(sum(self.grad_dims), n_tasks)if args.cuda:self.grads = self.grads.cuda()# allocate counters# 当前已观察到的任务集合self.observed_tasks = []self.old_task = -1# Ring buffer中已分配的内存self.mem_cnt = 0if self.is_cifar:# 每个任务应分配到的输出数self.nc_per_task = int(n_outputs / n_tasks)else:self.nc_per_task = n_outputs# 函数用于前向传播，根据当前任务t返回输出def forward(self, x, t):output = self.net(x)if self.is_cifar:# make sure we predict classes within the current taskoffset1 = int(t * self.nc_per_task)offset2 = int((t + 1) * self.nc_per_task)if offset1 > 0:output[:, :offset1].data.fill_(-10e10)if offset2 < self.n_outputs:output[:, offset2:self.n_outputs].data.fill_(-10e10)return output# 算法的主干部分# 更新内存：如果当前任务与上一个任务不同，将当前任务添加到已观察任务集合中，并更新任务编号。# 更新Ring Buffer中存储的当前任务的样本：计算需要更新的样本数量，将样本数据和标签拷贝到内存中，并更新内存下标。# 计算之前任务的梯度：对于已观察过的所有任务，先将参数梯度置为0，然后逐个任务进行前向传播和反向传播：计算损失并反向传播，将参数梯度存储起来。# 计算当前小批量数据的梯度：先将参数梯度置为0，然后进行前向传播和反向传播，计算当前任务的损失并反向传播，得到当前任务的梯度。# 检查梯度是否违反约束条件：如果有多个任务观察过，先拷贝当前任务的梯度，并计算当前任务梯度与之前任务梯度的点乘，如果点乘结果小于0（即违反约束），则对梯度进行相关处理。最后，使用优化器进行参数更新。def observe(self, x, t, y):# update memoryif t != self.old_task:self.observed_tasks.append(t)self.old_task = t# Update ring buffer storing examples from current taskbsz = y.data.size(0)endcnt = min(self.mem_cnt + bsz, self.n_memories)effbsz = endcnt - self.mem_cntself.memory_data[t, self.mem_cnt: endcnt].copy_(x.data[: effbsz])if bsz == 1:self.memory_labs[t, self.mem_cnt] = y.data[0]else:self.memory_labs[t, self.mem_cnt: endcnt].copy_(y.data[: effbsz])self.mem_cnt += effbszif self.mem_cnt == self.n_memories:self.mem_cnt = 0# compute gradient on previous tasksif len(self.observed_tasks) > 1:for tt in range(len(self.observed_tasks) - 1):self.zero_grad()# fwd/bwd on the examples in the memorypast_task = self.observed_tasks[tt]offset1, offset2 = compute_offsets(past_task, self.nc_per_task,self.is_cifar)ptloss = self.ce(self.forward(self.memory_data[past_task],past_task)[:, offset1: offset2],self.memory_labs[past_task] - offset1)ptloss.backward()store_grad(self.parameters, self.grads, self.grad_dims,past_task)# now compute the grad on the current minibatchself.zero_grad()offset1, offset2 = compute_offsets(t, self.nc_per_task, self.is_cifar)loss = self.ce(self.forward(x, t)[:, offset1: offset2], y - offset1)loss.backward()# check if gradient violates constraintsif len(self.observed_tasks) > 1:# copy gradientstore_grad(self.parameters, self.grads, self.grad_dims, t)indx = torch.cuda.LongTensor(self.observed_tasks[:-1]) if self.gpu \else torch.LongTensor(self.observed_tasks[:-1])dotp = torch.mm(self.grads[:, t].unsqueeze(0),self.grads.index_select(1, indx))if (dotp < 0).sum() != 0:project2cone2(self.grads[:, t].unsqueeze(1),self.grads.index_select(1, indx), self.margin)# copy gradients backoverwrite_grad(self.parameters, self.grads[:, t],self.grad_dims)self.opt.step()