本文主要是介绍UVa 11212 Editing a Book 编辑书稿 IDA* Iterative Deepening A Star 迭代加深搜剪枝,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目链接:Editing a Book
题目描述:
给定 n n n个( 1 < n < 10 ) 1<n<10) 1<n<10)数字,数字分别是 1 , 2 , 3 , . . . , n 1, 2, 3, ...,n 1,2,3,...,n,但是顺序是打乱的,你可以选择一个索引区间的数字进行剪切操作。问最少进行多少次剪切可以让这 n n n个数字变成升序。
例如 [ 1 , 2 , 4 , 3 ] [1, 2, 4, 3] [1,2,4,3]你可以选择剪切 3 3 3然后在 4 4 4的前面进行粘贴操作,那么该操作算一次剪切操作序列变得升序。
题解:
对于一个含有 n n n个数字的序列,要想让他变为升序,最多只需要进行 n n n次剪切操作一定能让序列升序(即每次都选择未剪切过的最大的数字剪切到开头,最多进行 n n n次操作,该序列一定变为有序)。那么我们可以依次枚举 [ 0 − n ] [0-n] [0−n]表示可能的答案,每次进行暴力搜索,如果某一次枚举的时候搜索成功,那么此时枚举的次数就是最小的操作次数。这就是 I D ID ID算法( I t e r a t i v e D e e p e n i n g Iterative Deepening IterativeDeepening迭代深搜)。因为直接搜索的话,我们每次需要枚举区间以及移动的位置,那么复杂度会达到 ( n 3 ) d e p t h (n ^3)^{depth} (n3)depth带入最大值 9 9 9的话算出来的值接近 6 × 1 0 25 6\times 10^{25} 6×1025很明显会超时。
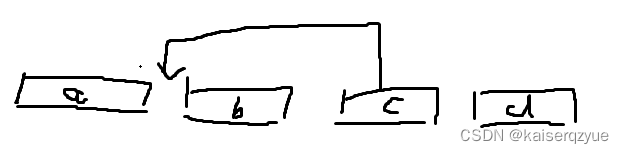
那么我们需要使用剪枝,如何进行剪枝呢?由于数字都是 1 − n 1-n 1−n的,那么我们可以记录每个数字的后一个数字不正确的个数即计算有多少个 i i i满足: a [ i ] + 1 ] ≠ a [ i + 1 ] a[i] + 1] \ne a[i +1] a[i]+1]=a[i+1],我们将这个数字记为 c n t cnt cnt,我们可以发现我们每一次剪切操作最多让 c n t cnt cnt减少 3 3 3。从下图我们可以看到如果我们进行一次剪切(下图中是把part c移到到part b的前面),后一个数字发生变化的位置有:a的最后一个元素,c的最后一个元素,b的最后一个元素。 也就是说在这种情况想最多只有三个数字的后一个元素会发生改变,当然其他情况也是可以同理推出来的。所以每一次剪切操作最多能够让 c n t cnt cnt减少 3 3 3,如果剩余的剪切操作在最优的情况下不能让 c n t cnt cnt小于 0 0 0,那么此时就应该停止搜索即: ( m a x D e p t h − n o w D e p t h ) ∗ 3 < c n t (maxDepth - nowDepth) * 3 < cnt (maxDepth−nowDepth)∗3<cnt。这也就是 A s t a r A\ star A star算法的思想,三部分合起来就叫做 I D A ∗ IDA* IDA∗。
实际上仅仅有上面的剪枝策略还是容易发生超时。而此时需要利用另外一种“贪心”策略:连续的升序区间不应该被执行剪切操作,也就是说对于一个序列里面类似于 [ 2 , 3 , 4 , 5 ] [2, 3, 4, 5] [2,3,4,5]的序列只能作为整体操作,而不应该只剪切其中的一部分。这似乎是显然的。
代码:
#include <bits/stdc++.h>using namespace std;int n, caseID = 1;
vector<int> number;int getCnt()
{int cnt = 0;for (int i = 0; i < n - 1; i++) {if (number[i] + 1 != number[i + 1]) { cnt++; }}return cnt;
}bool dfs(int nowDepth, int maxDepth)
{int cnt = getCnt();if (nowDepth == maxDepth) { return cnt == 0; }if ((maxDepth - nowDepth) * 3 < cnt) { return false; }for (int l = 0; l < n; l++) {if (l - 1 >= 0 && number[l] - 1 == number[l - 1]) { continue; }for (int r = l; r < n; r++) { // 枚举需要移动的区间的左右端点if (r + 1 < n && number[r] + 1 == number[r + 1]) { continue; }for (int k = r + 2; k <= n; k++) { // 枚举将区间移动到k前面vector<int> temp(number);vector<int> worker;for (int i = 0; i <= k - 1; i++) { // [0, k-1]移动if (l <= i && i <= r) { continue; }worker.push_back(number[i]);}for (int i = l; i <= r; i++) { worker.push_back(number[i]); } // [l, r]移动for (int i = k; i < n; i++) { worker.push_back(number[i]); } // 剩下部分移动number.swap(worker);if (dfs(nowDepth + 1, maxDepth)) { return true; };number.swap(temp);}}}return false;
}int main()
{ios::sync_with_stdio(false);while(cin >> n && n != 0) {number.resize(n);for (int i = 0; i < n; i++) { cin >> number[i]; }for (int maxDepth = 0; ; maxDepth++) {if (dfs(0, maxDepth)) {cout << "Case " << caseID << ": " << maxDepth << endl;caseID++;break;}}}return 0;
}
这篇关于UVa 11212 Editing a Book 编辑书稿 IDA* Iterative Deepening A Star 迭代加深搜剪枝的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!