图神经网络 Graph Neural Networks:Foundations, Frontiers, Applications 基于 node2vec 的电影推荐实验

目录

0.概念

1.引言

（1）图神经网络概述

（2）图嵌入

（3）图神经网络类型

（4）图神经网络典型应用

2. 图嵌入：基于图结构的表示学习

（1）node2vec 原理

3.工具包 node2vec 的使用

4.案例：基于 node2vec 的电影推荐

5.总结

---

0.概念

    Graphs are a general language for describing and modeling complex systems.

 

图形结构化数据无处不在：

   Social networks，Information retrieval，Biomedical graphs，Scene graphs

发展时间线：

   图基本模块定义

    V：点，每个点都有自己的特征向量（特征举例：邻居点数量、一阶二阶相似度）
    E：边，每个边都有自己的特征向量（特征举例：边的权重值、边的定义）
    U：整个图，每个图都有自己的特征向量（特征举例：节点数量、图直径）

    图神经网络要做的事情

• 为每个节点整合特征向量，根据其对节点做分类或者回归
• 为每条边整合特征向量，根据其对边做分类或者回归
• 为每张图整合特征向量，根据其对图做分类或者回归

 Feature Learning in Graphs

      为图中的机器学习设计高效的任务无关/任务相关特征学习！

Graph Neural Networks: Foundations

  •Learning node embeddings:

•Learning graph-level embeddings:

 Graph Neural Networks: Basic Model

    • Key idea: Generate node embeddings based on local neighborhoods.

 Neighborhood Aggregation

   Intuition: Network neighborhood defines a computation graph

                                              

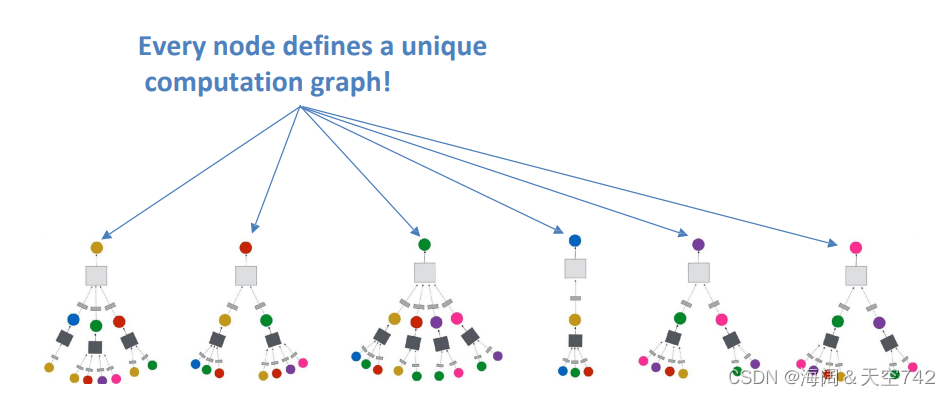
节点在每一层都有嵌入;  模型可以是任意深度;  节点i的“第0层”嵌入是其输入特征，即xi;

          

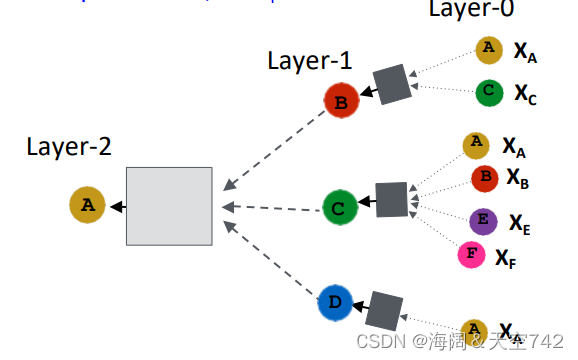
 Overview of GNN Model

     

       

 

 GNN Model: A Case Study

        Basic approach: Average neighbor information and apply a neural network.

         

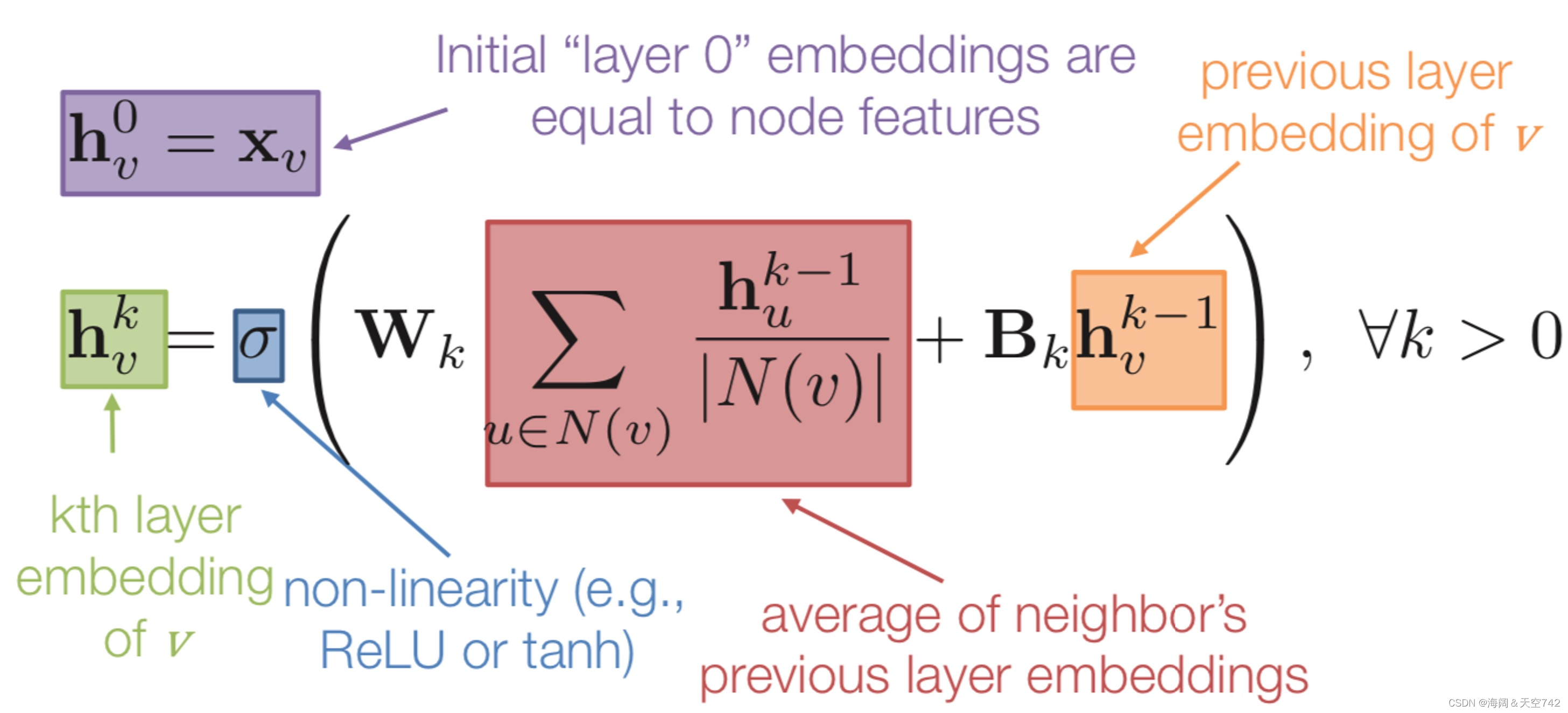
 GNN Model: Quick Summary

    Key idea: generate node embeddings by aggregating neighborhood information.

 图神经网络：经典模型

Supervised Graph Neural Networks	Unsupervised Graph Neural Networks
Spectral-based Graph Filters • GCN (Kipf & Welling, ICLR 2017), Chebyshev-GNN (Defferrard et al. NIPS 2016)	Variational graph auto-encoders (Kipf and Welling, 2016)
Spatial-based Graph Filters • MPNN (Gilmer et al. ICML 2017), GraphSage (Hamilton et al. NIPS 2017) • GIN(Xu et al. ICLR 2019)	Deep graph infomax (Velickovic et al, 2019)
Attention-based Graph Filters • GAT (Velickovic et al. ICLR 2018)

Recurrent-based Graph Filters • GGNN (Li et al. ICLR 2016)

图卷积网络(GCN)

    关键思想：图上的谱卷积

    

 Message Passing Neural Network (MPNN) 消息传递网络

  关键思想：图卷积作为一个消息传递过程

 Graph Attention Network (GAT)

  关键思想：在执行消息传递时动态学习边缘的权重（注意力得分）

   

Gated Graph Neural Networks (GGNN) 

   关键思想：在考虑边缘类型和方向的同时使用门控递归单元

    

1.引言

（1）图神经网络概述

    近几年来，基于计算资源的快速发展以及大量训练数据的可获得性等原因，引发了神经网络的快速兴起与应用，并成功地推动了计算机视觉领域（Computer Vision, CV）与自然语言处理领域（Natural Language Processing, NLP）的发展与兴盛。曾经严重依赖于手工提取特征的机器学习模式，如今都已被各种端到端的深度学习范式所取代，如卷积神经网络（CNN）、长短期记忆网络（LSTM）、自注意力机制（self-attention），如下图所示为基于自注意力机制的前沿模型 Transformer：

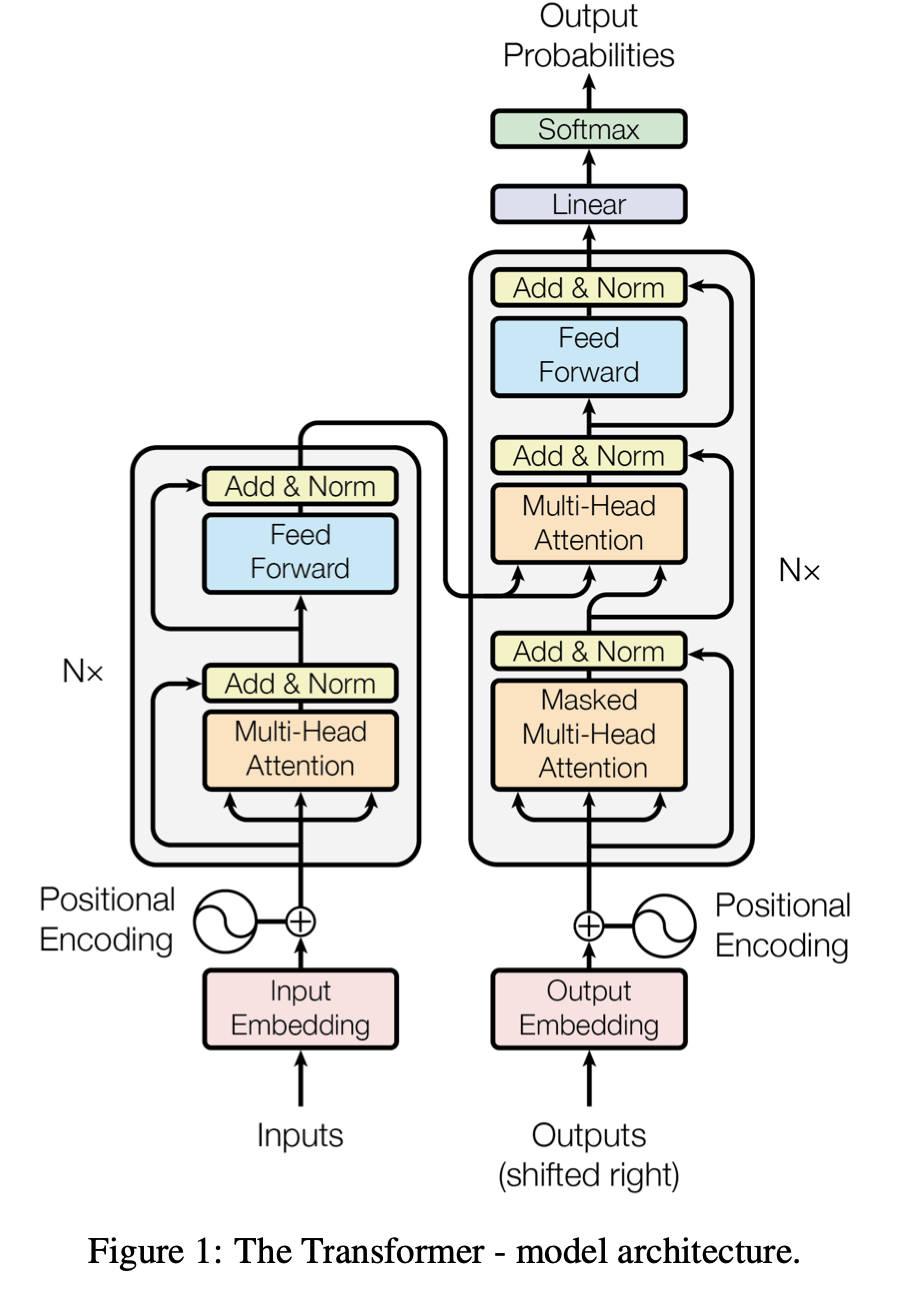
     神经网络的不同模型基于不同的数据结构展开，例如，图像的本质为上下左右相连的像素值；而时间序列（语音、文本等）则由元素单向连接而成。对于图像处理，CNN 是目前的基础结构，对于时间序列，RNN 是基础结构，而 self-attention 机制是目前的集大成者。

     以上所提到的均是欧氏空间数据，神经网络在其特征表征方面取得了可观效果，但在许多实际应用场景中，数据从非欧式空间生成，元素和元素之间，是一个互相联系的复杂网络，这时候应当用节点和连接它们的边来描述这种数据类型，比如，社交网络（用户为节点，关系为边）、交通网络（地点为节点，交通工具行驶路径为边）、化学分子（原子为节点，化学键为边）等等，这时候一般的神经网络便难以适用了。主要原因在于：

• 图数据是不规则的，图中的每个节点都有不同数量的相邻节点，导致一些重要的操作（例如卷积）在规则的图像上很容易计算，但不再适合直接用于图；
• 大部分神经网络模型的一个核心假设是，数据样本之间彼此独立。然而，对于图来说，情况并非如此，图中的每个数据样本（节点）都会经由边与图中其他数据样本（节点）相关联，而这些信息不可或缺，可用于捕获实例之间的相互依赖关系。

图相关的分析任务可以大致抽象为以下几类:

• 节点分类：基于其他标记的节点和网络拓扑来确定节点标签，比如，在社交网络图中确定哪些人是“大 V”。
• 链接预测：预测缺失链路或未来可能出现的链路，比如，预测社交网络中某两个人可能存在关联，从而进行“可能认识的人”的推荐。
• 图分类：任务不依赖于某个节点或某条边的属性，而是需要考虑整张图的信息，从而确定整图的标签，比如，预测某分子结构是否有变异性。
• 聚类：发现相似节点的子集，并将它们分组在一起，比如，将社交网络中的人群进行分类，从而进行基于社交的商品推荐。
• 可视化：为了更深入直观地了解网络结构，如何对图进行表示的相关技术。

（2）图嵌入

     图神经网络=图+神经网络。而图嵌入发展较早，在早期是一个相对独立的领域，但在近期，人们开始基于图神经网络进行图嵌入的学习，因此可以说，图嵌入的表示应用了图神经网络。

     什么是嵌入（Embedding）？嵌入在数学上是指，将一个空间的点映射到另一个空间，通常是从高维抽象的空间映射到低维的具象空间。

     意义：高维数据转换到低维有利于有效的特征表征以及算法的处理。而图嵌入是指在保留图的网络拓扑结构和节点内容信息的基础上，找到一种映射函数，该函数将网络中的每个节点转换为低维度的潜在表示，如下图所示（左图中的每个节点基于特征的数目，可由多维向量来表征）：

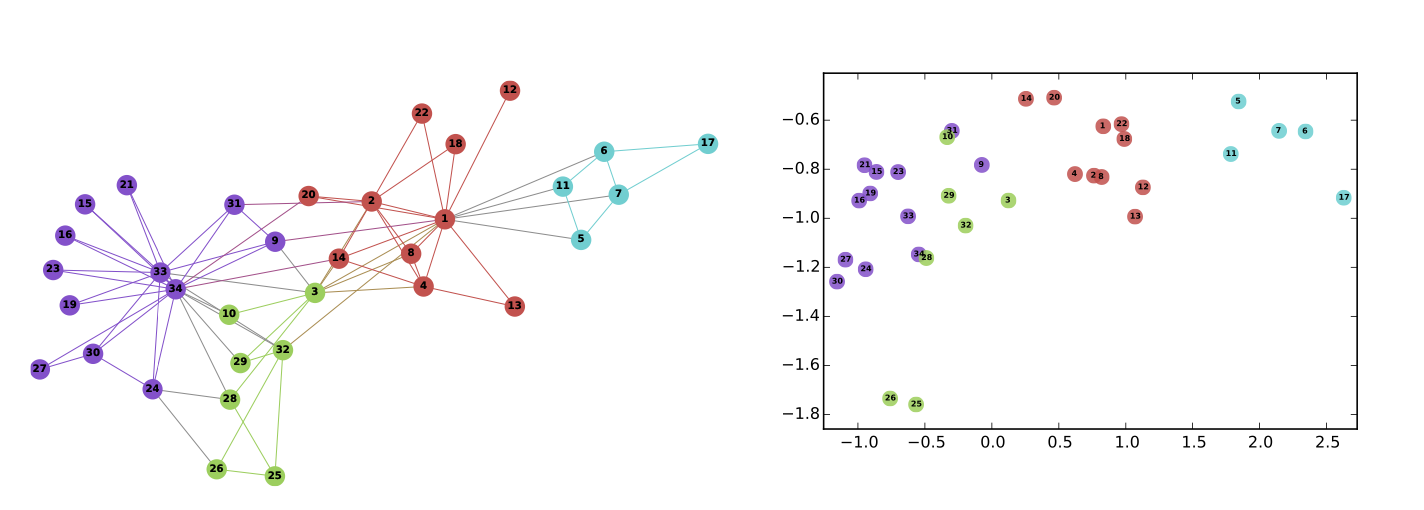
 图嵌入的方法大致可以划分为三大类别：

矩阵分解	较传统的方法，计算量大，包括 Locally Linear Embedding、Laplacian Eigenmaps、Cauchy graph embedding、Structure Preserving Embedding、Graph Factorization 等方法。
随机游走	主要借鉴了 NLP 中 word2vec 的思想，包括 DeepWalk、node2vec、 Hierarchical representation learning for network、Walklets 等方法。
深度学习方法	在这里，图嵌入的深度学习方法也属于图神经网络，比如 Structural deep network embedding、Deep neural networks for learning graph representations 等 。

         简单介绍随机游走方法

   对于 NLP 中的 word2vec，其本质是根据语料库中单词的共现关系训练出每个单词的嵌入，常用的 word2vec 模型有 CBOW 和 Skip-gram 两种，CBOW 根据上下文预测中心词，而 Skip-gram 根据中心词预测上下文，训练完成的模型中的隐层参数矩阵即为词向量，如下图所示：

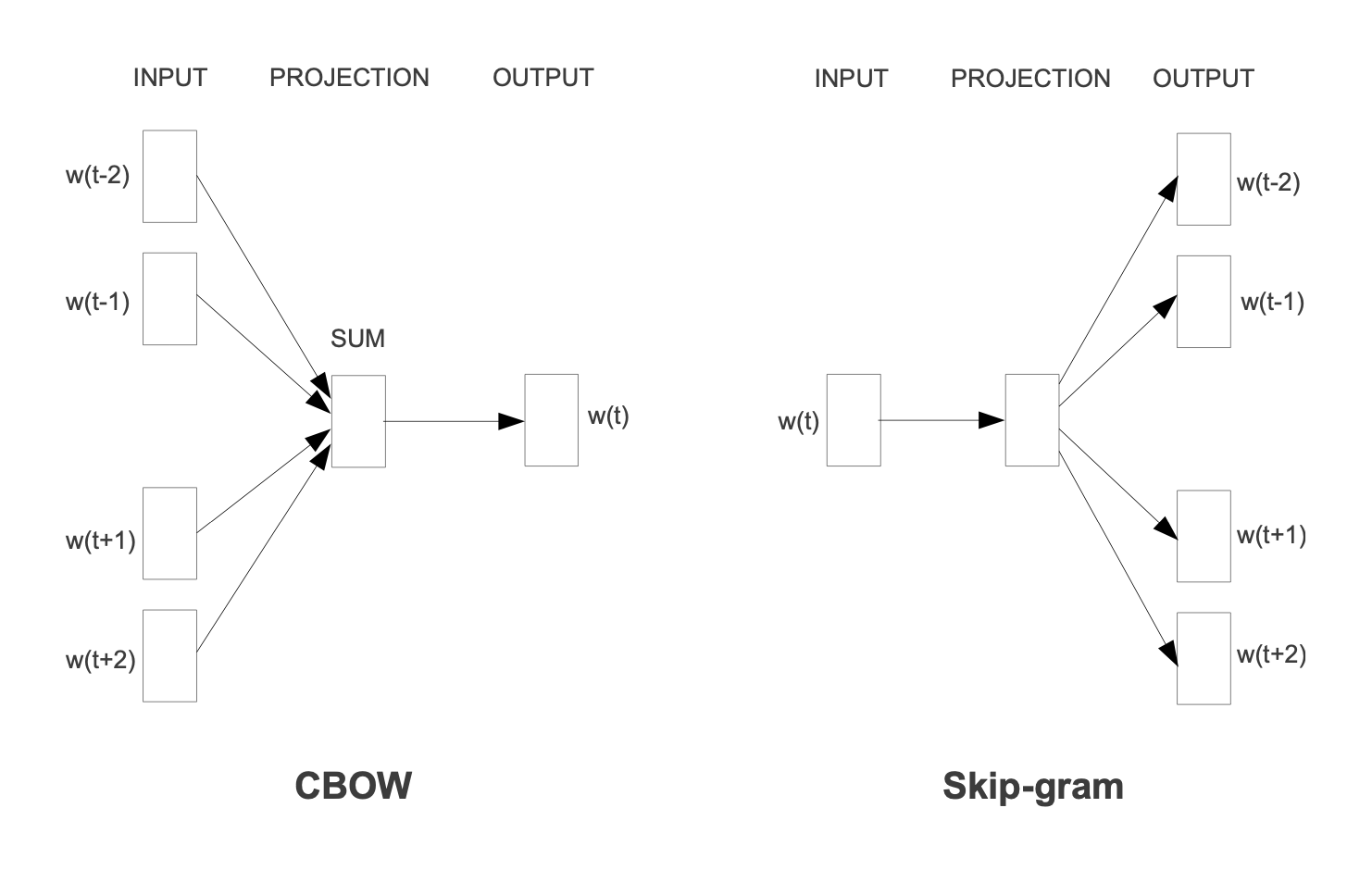
      既然单词可以通过共现关系进行嵌入的表示学习，那么，将图类比成整个语料库，图中的节点类比成单词，是否也可以通过共现关系对图中的节点进行嵌入表示呢？另一个问题则是，对于图，这种共现关系如何描述呢？随机游走的方法主要解决了此问题。

     其中，DeepWalk 和 node2vec 是此类方法的典型代表。DeepWalk 方法首先选择某一特定点为起始点，根据随机游走得到点的序列，然后将这个得到的序列应用与 word2vec 中类似的损失函数来学习，最终训练得到各点的嵌入表示。

      以电商中的商品推荐为例，如下图所示，首先根据用户的购物行为（a）构建出一个图网络（b），随后通过随机游走采样的方式构建出节点序列（例如：一开始在 A 结点，A->B，B 又跳到了它的邻居节点 E，最后到 F，得到 "A->B->E->F" 序列）；在产生多个序列（c）后，便可以采用 Skip-gram 的模型（d）的方式来得到最终的节点向量，通过最大化随机游走得到的序列中的节点出现的概率来保持节点之间的高阶邻近性。

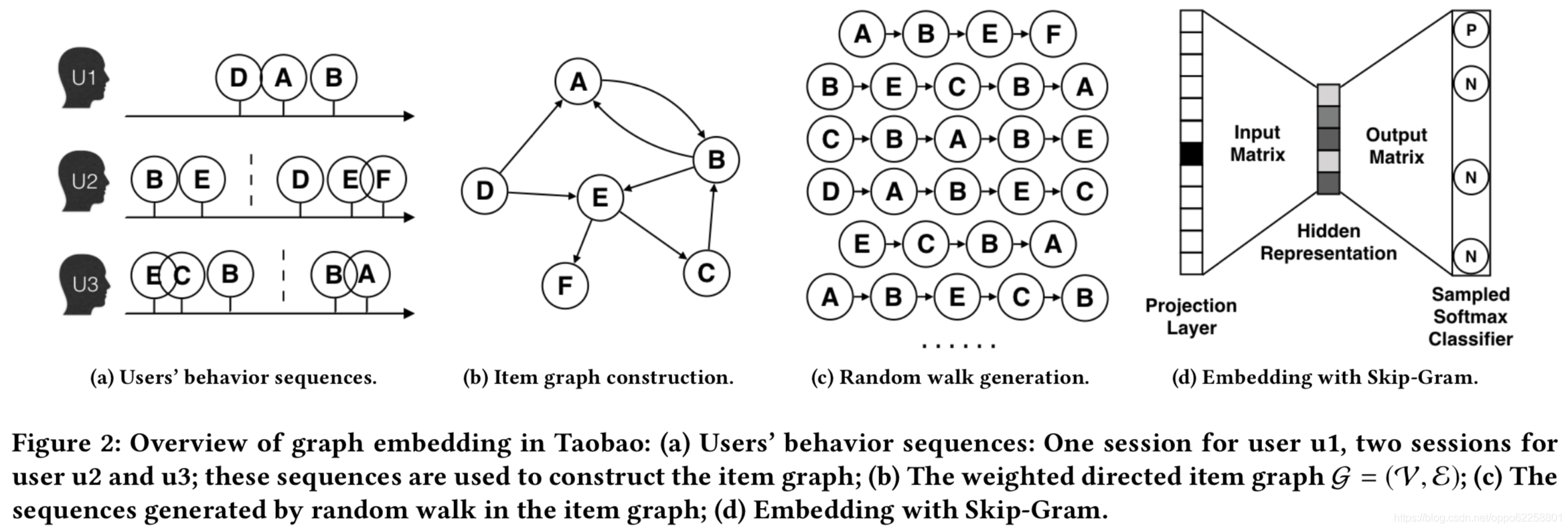
       而与 DeepWalk 基本原理相似的 node2vec 采用了有偏随机游走来采样生成序列，在广度优先搜索（BFS）和深度优先搜索（DFS）之间进行权衡，从而产生比 DeepWalk 更高质量和更多信息量的嵌入。

（3）图神经网络类型

• 图卷积网络（Graph Convolution Networks，GCN）：是一种非常基本的图神经网络结构，将卷积运算从传统数据（例如图像）推广到图数据，其核心是学习一个函数映射，使得图中的节点可以聚合自身特征以及邻居特征，进而生成节点的新表示。GCN 又分为谱域 GCN（Spectral）和空域 GCN（Spatial），其中谱域 GCN 发展较早，主要思想基于图的信号处理，理论方面较难理解，对数学要求较高，但是现在主流方法以空域 GCN（Spatial）为主，因此对前者的学习可量力而行。
• 图注意力网络（Graph Attention Networks）：在图数据学习过程中使用注意力，放大数据中重要的部分的影响，典型代表有 Graph Attention Network (GAT)、Gated Attention Network (GAAN)、Graph Attention Model (GAM)。其中，GAT 和 GAAN 本质上也属于图卷积网络，特点有于它们能够自适应地学习邻居节点的重要性权重。
• 图生成网络（ Graph Generative Networks）：顾名思义，此类网络的目标是在给定一组观察到的图的情况下生成新图。图生成网络的许多方法都是特定于领域的。主要方法有，将生成过程作为节点和边的交替形成因素，或者采用生成对抗训练。
• 图自编码器（ Graph Autoencoders）：指图嵌入方法，其目的是利用神经网络结构将图的顶点表示为低维向量。
• 图时空网络（Graph Spatial-temporal Networks）：同时捕捉时空图的时间与空间相关性。例如，在交通网络中，每个传感器作为一个节点连续记录某条道路的交通速度，其中交通网络的边由传感器对之间的距离决定。图形时空网络的目标可以是预测未来的节点值或标签，或者预测时空图标签。一般将 GCN 与 RNN 或 CNN 结合使用，进行特定任务的处理。

（4）图神经网络典型应用

       图神经网络可以说是处于风口的一项新兴技术，业界普遍认为，其有望解决当前传统神经网络无法处理的因果推理、可解释性等一系列瓶颈问题，是未来神经网络领域的重点研究方向。那么，图神经网络有哪些应用呢？

      1）自然语言处理（NLP）

      GNN 在自然语言处理中的应用包括多跳阅读（Multi-hop Reasoning）、实体识别、关系抽取以及知识图谱中的关系补全或预测等。其中，多跳阅读是指在阅读理解的过程中，需要在多篇文档之间进行多级跳跃式的关联与推理，才能找到正确答案，相较传统单文档问答数据集，更具有开放性与挑战性（如下图所示）。要完成多跳推理任务，离不开对语义实体的识别以及实体之间关系的抽取，而 GNN 能对表征语义关系的网络进行整体建模，学习更加复杂与丰富的语义信息，极大地提高了推理能力。

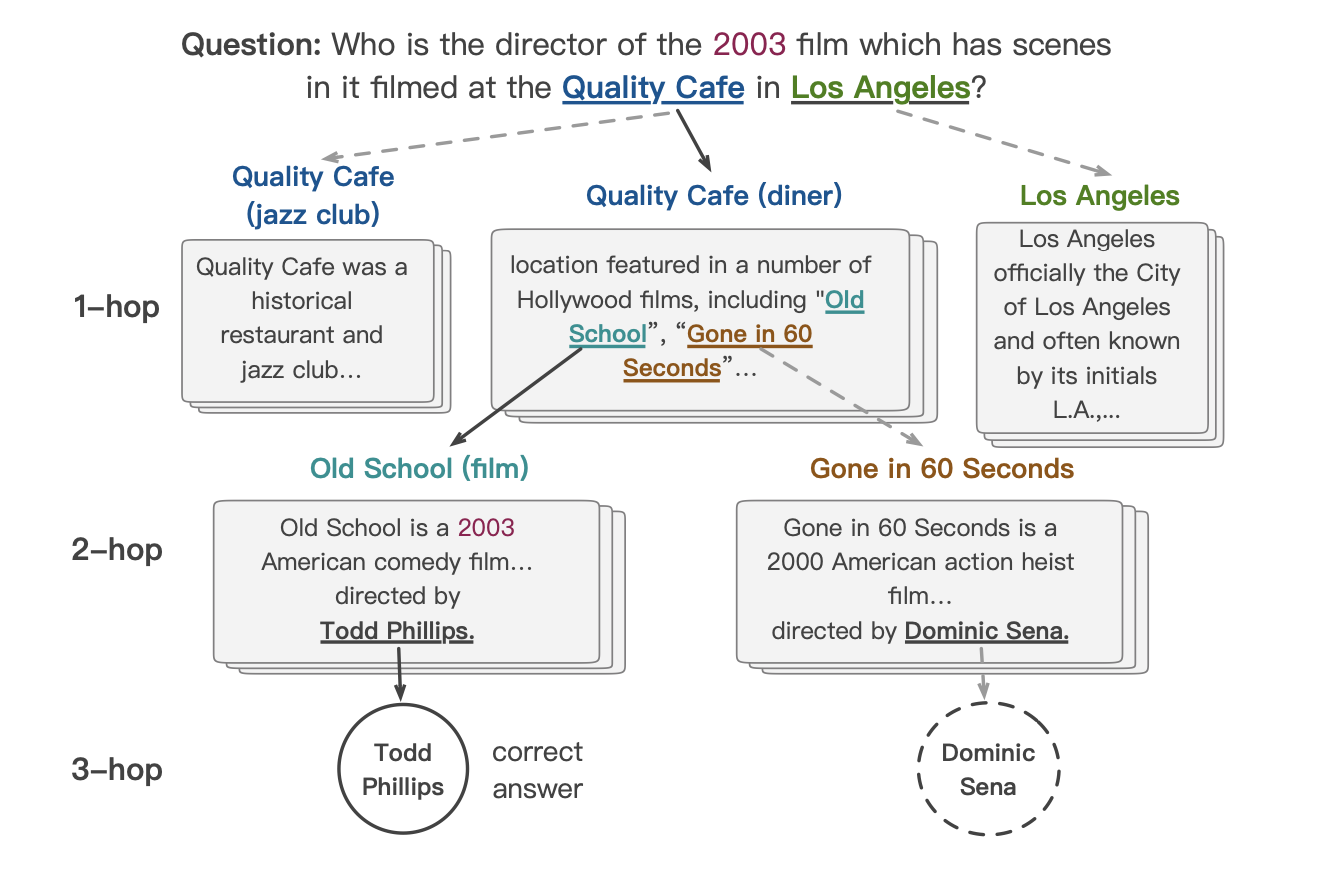
 2） 计算机视觉（CV）

    GNN 在计算机视觉中的应用包括场景图生成、点云分类与分割、动作识别、视觉推理等多个方面。例如，点云数据是 3D 视觉中一种十分常见的数据表示方法，其通常由一组坐标点（x,y,z）表示，映射了现实世界中物体的特征（如下图所示为巴黎圣母院的点云图），因此存在一种内在的表征物体语义的流行结构，而这种结构的学习也正是 GNN 所擅长的。又如，在动作识别中，识别视频中包含的人类动作有助于机器更好地理解视频内容。首先，检测视频剪辑中人体关节的位置，再由骨骼连接的人体关节自然形成图表。如此，给定人类关节位置的时间序列，便可以应用时空神经网络来学习人类行为模式。

 3）推荐系统

     推荐一直是各大互联网公司十分重要的营收手段，如何在推荐系统中有效地融入额外的信息，如用户端社交网络的信息、商品端商品知识图谱的信息等，一直是学界和工业界的研究热点。由于大部分信息本身为错踪复杂的网络结构，图神经网络能够从多方面赋能推荐。比如，用户的购买行为会受到其社交圈的影响，而社交圈可以基于图神经网络进行建模。

4）交通网络

    随着现代化的进程，交通拥堵越来越成为现代城市建设的一个热点难题。准确地预测交通网络中的交通速度、交通量或道路密度，在路线规划和流量控制中至关重要。基于图的时空神经网络方法或许可用来解决这些问题。例如，将交通网路建模为时空图，节点为放置在道路上的传感器，边由阈值以上成对节点的距离表示，每个节点都包含一个时间序列作为特征，目标是预测一条道路在时间间隔内的平均速度。

2. 图嵌入：基于图结构的表示学习

     将网络中的节点（或边）用向量来表征，是一些基本任务，比如网络节点的分类或者链接预测的关键步骤。在本实验中，我们将学习如何基于经典的 node2vec 方法对图中的节点进行有效表征（又称为图嵌入）。

（1）node2vec 原理

      在以复杂网络为基础的数据中，存在一些基本的任务，比如网络节点的分类，也就是将网络中的节点进行聚类，我们关心的是哪些节点具有类似的属性，就将其分到同一个类别中；再比如链接预测， 它的目标是根据已知的节点和边，得到新的边（的权值/特征），也就是预测网络中哪些顶点有潜在的关联。

     要完成诸如以上所述的这些任务，首先要解决的问题便是，如何有效地表示网络嵌入，将网络中的节点（或边）用向量来表征。要设计出能保持节点邻居信息而且又容易训练的模型，Aditya Grover 和 Jure Leskovec 在 2016 年提出了 node2vec, 尝试解决了上述方法的困境。作者认为，节点在网络中中的相似性体现在以下两大方面：

• 很多节点会聚集在一起，这些聚集的点称之为社区（homophily），同一社区内的点具有相似性。
• 网络中两个可能相聚很远的点，在边的连接上有着类似的特征，即结构相似。

    比如在下图中，u,s1​,s2​,s3​,s4​ 就属于一个社区，从邻近的角度而言具备相似性，而 u,s6​ 在结构上有着相似的特征，即结构相似：

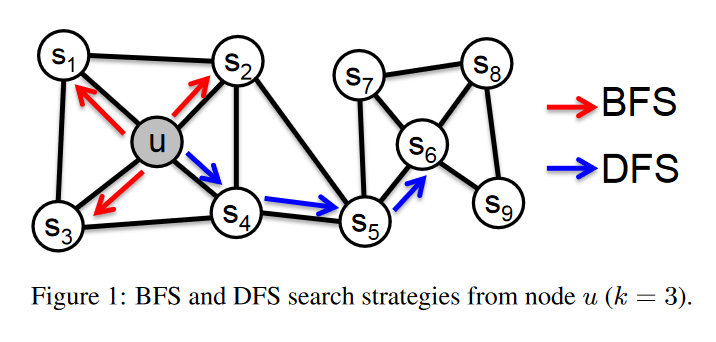
 基于以上逻辑，要设计的网络表示学习算法的目标必须满足以下两点：

• 同质性：同一个社区内的节点表示相似。
• 结构相似性：拥有类似结构特征的节点表示相似，值得注意的是，结构相似的两个点未必相连，可以是相距很远的两个节点。

    图嵌入的学习无非是基于节点之间的联系去进行表征学习，这和自然语言处理 (Natural Language Processing，NLP) 中的 word2vec 非常类似，可以把单词看作节点，单词的周边词汇当作相邻节点。因此，作者借鉴了 word2vec 的训练模型 Skip-gram 的思路，基于当前节点与邻居节点的关系对图嵌入进行训练，损失函数如下：

                               

    其中，f(u) 是当前节点，Ns​(u) 是其邻居节点（以 s 的方式采样得到），为了简便计算，类似 Skip-gram，又引入了两个假设：

• 条件独立（Conditional independence），即采样到的每个邻居相互独立，所以如果要计算采样所有邻居的概率只需要将采样的每个邻居的概率相乘即可。公式表示如下：

                        

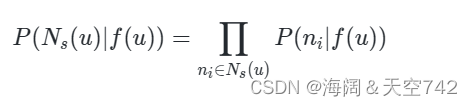
• 特征空间的对称性（Symmetry in feature space），假如一条边连接了 a 和 b，那么映射到特征空间时，a 对 b 的影响和 b 对 a 的影响应该是一样的。

   Ns​(u) 未必是 u 的直接邻居点，只是用 s 方法采样得到的邻居，跟具体的采样方法有关。

    作者首先分析了两种图的游走方式，深度优先游走（Depth-first Sampling，DFS）和广度优先游走（Breadth-first Sampling，BFS）。

• BFS 倾向于在初始节点的周围游走，可以反映出一个节点邻居的微观特性；
• 而 DFS 一般会跑得离初始节点越来越远，可以反映出一个节点邻居的宏观特性。

     能否综合 DFS 和 BFS 的游走方式进行邻居节点采样，既反映节点的微观特性又反映其宏观特性呢？作者引入了两个参数用来控制游走的方式。

     对于一个采样过程中的随机游走，如果上一步采样了 t，而且现在停留在节点 v 上，那么下一个要采样的节点 x 是哪个呢？

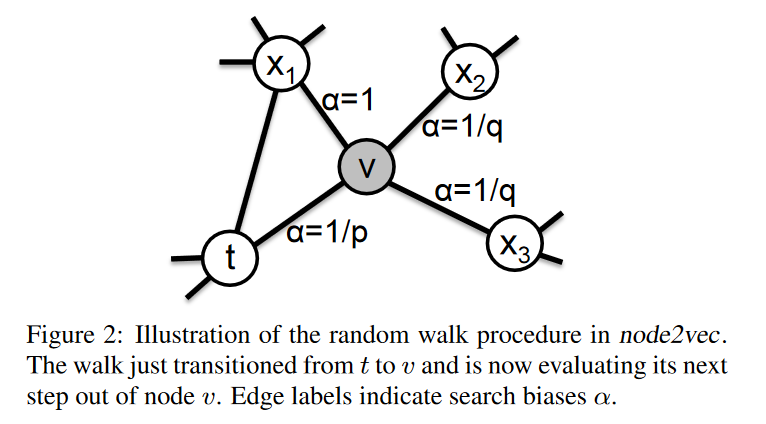
    作者定义了一个权重分布（在这里指的是，一个节点到它的不同邻居的未归一化的转移概率，因此以下和不为 1）：

• 如果 t 即 x，那么采样 x 的权重为 1/p；
• 如果 t 与 x 相连，那么采样 x 的权重为 1；
• 如果 t 与 x 不相连，那么采样 x 权重为 1/q。

  参数 p、q 的意义分别如下：

• 返回概率 p（return rate）：控制重复访问刚刚访问过的节点的概率。如果 p 越大（1/p 会越小），那么采样会尽量不往回走，对应上图的情况，就是下一个节点不太可能是上一个访问的节点 t；如果 p 越小，那么采样会更倾向于返回上一个节点，这样就会一直在起始点周围某些节点来回转来转去。
• 出入参数 q（exploration rate）：控制着游走是向外还是向内。如果 q 越大（1/q 会越小），那么游走会倾向于在起始点周围的节点之间跑，可以反映出一个节点的 BFS 特性；如果 q 越小（1/q 会越大），那么游走会倾向于往远处跑，反映出 DFS 特性。

     通过调节参数 p、q，我们可以设计出不同倾向的游走方式，继而采样出不同的样本对，后续再应用于图嵌入的训练。当 p=q=1 时，去各个点的概率相等，即为随机游走方式。

3.工具包 node2vec 的使用

    首先利用 networkx 随机初始化一个图数据：

import networkx as nx
from matplotlib import pyplot as plt
# 生成一个 G(n,p) 图，其中参数 n 表示有 n 个点，p 表示两个点之间是否连接的概率
graph_example = nx.fast_gnp_random_graph(n=50,p=0.3)nx.draw(graph_example)
plt.show()

结果（可视化数据）：

  

接下来进行图嵌入的训练，调用 node2vec.node2vec 中的 Node2Vec 即可，主要存在以下几个重要参数：

重要参数	说明
graph	networkx 表示的图数据，节点名称类型必须为 integer 或者 string，模型训练完成后节点名称类型均为 string。
dimensions	节点的嵌入维度，默认为 128
walk_length	游走的节点数，默认为 80
num_walks	每个节点的游走次数，默认为 10
p	return rate 参数 p
q	exploration rate 参数 q
workers	并行数

构建模型：

from node2vec.node2vec import Node2Vec 
node2vec_example = Node2Vec(graph=graph_example, dimensions=64, walk_length=30, num_walks=200, workers=4)

 node2vec 模型训练：

model_example = node2vec_example.fit(window=10, min_count=1, batch_words=4)

获取某个节点的嵌入(这里随机初始化的节点名称默认为数字)：

model_example.wv['3']

[ 0.16296327 -0.064733    0.31033048 -0.02240712  0.07323866 -0.07557924-0.10728993 -0.17278731  0.09826993 -0.09025497  0.14007017  0.05262498-0.10548531 -0.05886989  0.12315977  0.05687659  0.14811924 -0.15225178-0.09110078  0.03357899  0.13562164  0.15579402  0.2382454  -0.163913130.07071597  0.210301   -0.22581449 -0.03374222  0.17397945 -0.29411703-0.11668402  0.29578972 -0.04581077 -0.07105486 -0.07536785  0.026976230.11204905  0.15567993  0.09604602  0.07359116 -0.04120783 -0.016491670.24241725 -0.32728148 -0.12040729 -0.11995523 -0.01413647 -0.14618422-0.00721072  0.17487918  0.16142212 -0.07215199  0.06512492  0.10168155-0.20139512  0.1380023  -0.00098967 -0.06365409 -0.08948215 -0.0308280.06372829 -0.15223545 -0.02057695 -0.00462567]

获取某个节点的相似节点：

model_example.wv.most_similar('3')

[('22', 0.5553644299507141), ('18', 0.5418640971183777), ('9', 0.512002170085907), ('24', 0.505357563495636), ('42', 0.5022357702255249), ('15', 0.48660793900489807), ('34', 0.4858168661594391), ('33', 0.4841001331806183), ('29', 0.476712167263031), ('12', 0.4755667746067047)]

4.案例：基于 node2vec 的电影推荐

      我们也可以对自定义的真实图数据进行图嵌入的训练，并应用于下游任务，比如在以下案例中，我们将对一个电影的网络数据进行训练，并且基于训练好的模型进行相似电影的推荐。

      首先准备好数据，

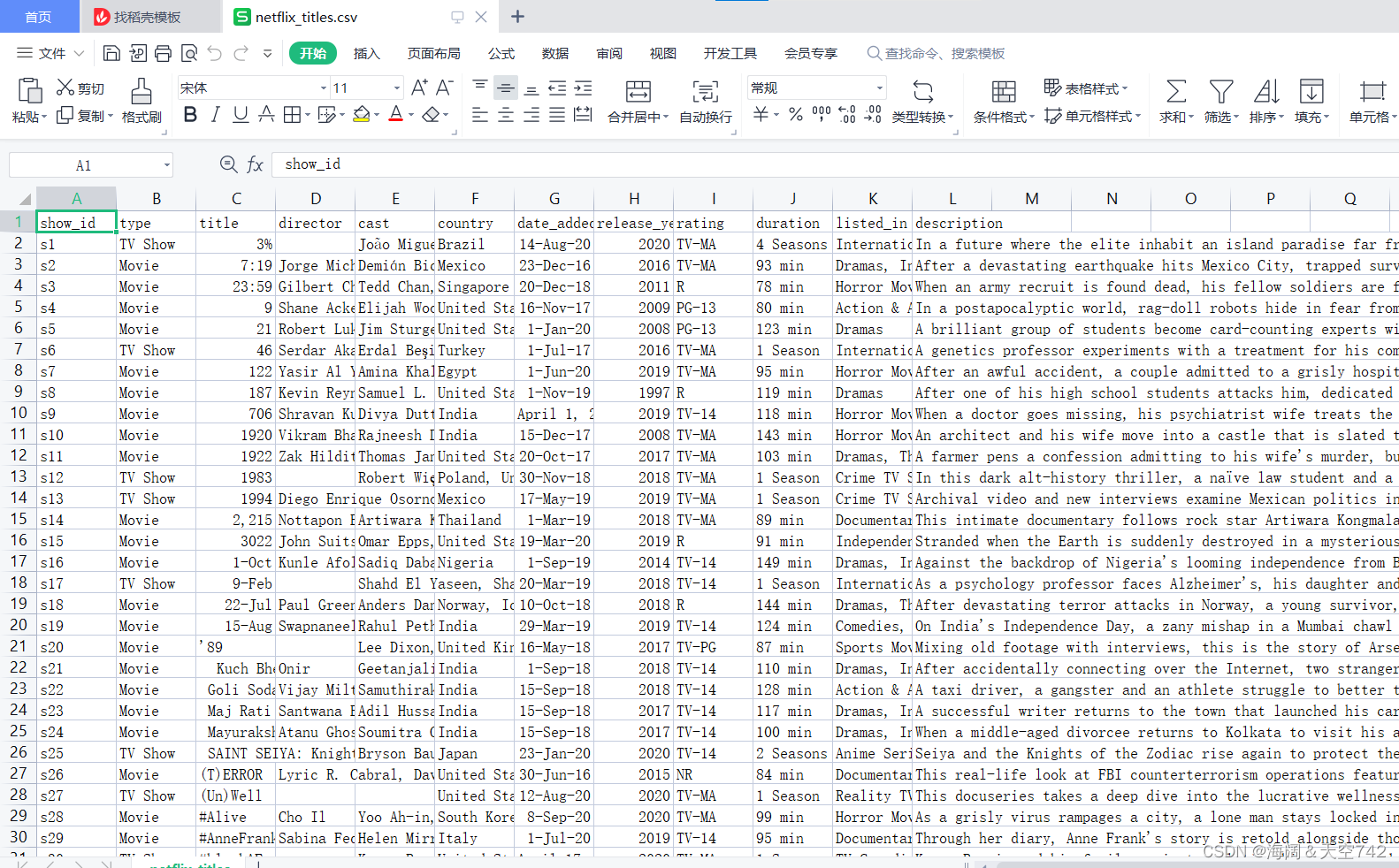
 加载并预处理数据：

import pandas as pdnetflix_df = pd.read_csv("netflix_titles.csv")
netflix_df = netflix_df.dropna() # 丢弃含有缺失值的行
netflix_df = netflix_df.drop(['description'],axis=1) # 去除 description 列
netflix_df.tail()

基于以上数据中的电影名称（title）以及电影类型（genre）构建图。首先定义图构建函数

def create_graph(df):graph = nx.Graph() #建立空图for movie_title in df['title']:#获取影片类型genres = df[df['title'] == movie_title]['listed_in'].values[0].rstrip().lower().split(',')for genre in genres: #构建电影与类型间的链接graph.add_edge(movie_title.strip(),genre)return graph

构建图：

netflix_graph = create_graph(netflix_df)

查看电影 Zoom 的度数（指和该顶点相关联的边数）：

netflix_graph.degree()['Zoom']

查看类型 dramas 的度数：

netflix_graph.degree()['dramas']

训练图嵌入：

netflix_node2vec = Node2Vec(netflix_graph, dimensions=20, walk_length=16, num_walks=10)
netflix_model = netflix_node2vec.fit(window=5, min_count=1)

通过以上步骤，我们完成了电影图数据的图嵌入训练，并基于此根据与某电影最相似的电影，可进行电影推荐，例如，获取如电影 Zombieland 最相关的电影：

netflix_model.wv.most_similar('Zombieland')

[('Scary Movie', 0.9874622225761414), ('Little Evil', 0.9870952367782593), ('The Babysitter', 0.9860270619392395), ('Vampires vs. the Bronx', 0.9822988510131836), ('A Haunted House', 0.9821882843971252), ('Holidays', 0.9743597507476807), ('The Babysitter: Killer Queen', 0.9725714921951294), ('Hubie Halloween', 0.9664759039878845), ('He Never Died', 0.9655413627624512), ('Target', 0.9612836837768555)]Process finished with exit code 0

     当然，在以上的电影图数据中，相关的信息较少（仅有类型），还可以添加更多信息，比如电影演员、电影导演、电影票房、电影语言、电影国家等等，构建更丰富信息的图数据，进而进行更加可靠的电影推荐。

5.总结

   node2vec 的原理和 word2vec 十分类似，当然，word2vec 只需要通过滑动窗口的设定直接找到邻居单词，而在 node2vec 中，邻居节点并不一定都是与当前节点相连的点，也有可能是相距较远，但具备相似结构的节点，因此，node2vec 的邻居节点的采样方式相对比较复杂，综合了 DFS 以及 BFS 的特性。