【优化求解】基于狮群算法LSO求解最优目标matlab源码

1 简介

狮群优化算法（Loin Swarm Optimization, LSO），是于2018年提出的一种新型智能优化算法。基于狮群中狮王、母狮及幼狮的自然分工,模拟狮王守护、母狮捕猎、幼狮跟随3种群智能行为,提出群体智能算法——狮群算法.算法中不同种类的狮子位置更新方式不同.遵循自然界生物"适者生存"的竞争法则,狮王守护领土,优先享用食物,母狮合作捕猎,幼狮分为学习捕猎、饥饿进食和成年被驱逐.狮子位置更新方式的多样化保证算法快速收敛,不易陷入局部最优.最后,将算法应用于6个标准测试函数优化问题,并对比粒子群算法、骨干粒子群算法,测试结果表明,文中算法收敛速度较快,精度较高,能较好地获得全局最优解.

​

2 部分代码

%_________________________________________________________________________%
% 狮群优化算法             %
%_________________________________________________________________________%% 使用方法
%__________________________________________
% fobj = @YourCostFunction       设定适应度函数
% dim = number of your variables   设定维度
% Max_iteration = maximum number of generations 设定最大迭代次数
% SearchAgents_no = number of search agents   种群数量
% lb=[lb1,lb2,...,lbn] where lbn is the lower bound of variable n 变量下边界
% ub=[ub1,ub2,...,ubn] where ubn is the upper bound of variable n   变量上边界
% If all the variables have equal lower bound you can just
% define lb and ub as two single number numbers% To run SSA: [Best_pos,Best_score,curve]=LSO(pop,Max_iter,lb,ub,dim,fobj)
%__________________________________________clear all 
clc
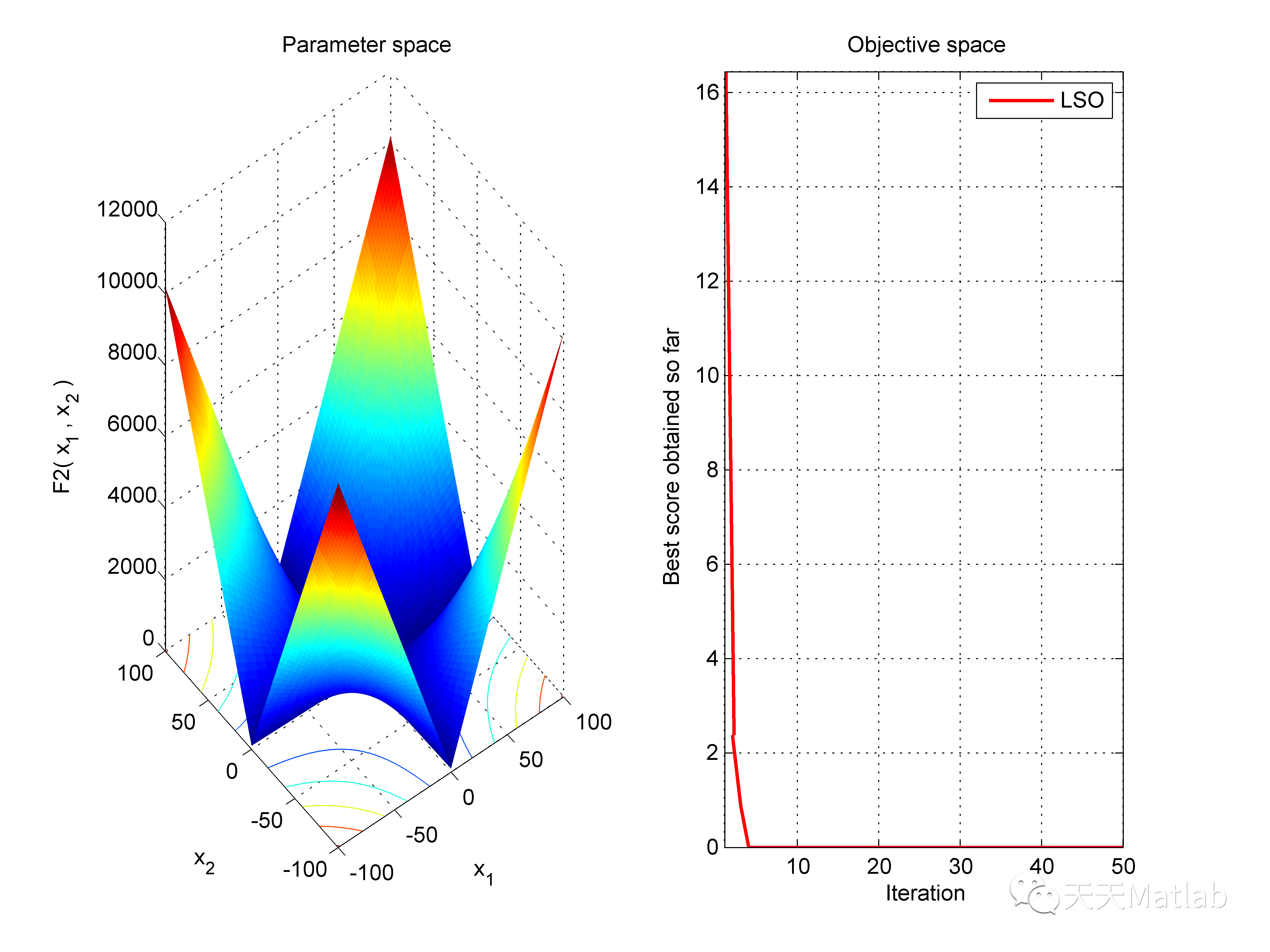
SearchAgents_no=30; % 种群数量Function_name='F2'; % F1 to F23 设定适应度函数Max_iteration=50; % 设定最大迭代次数% 获取适应度函数边界信息等
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);  %设定边界以及优化函数[Best_score,Best_pos,LSO_curve]=LSO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj); %开始优化figure('Position',[269   240   660   290])
%Draw search space
subplot(1,2,1);
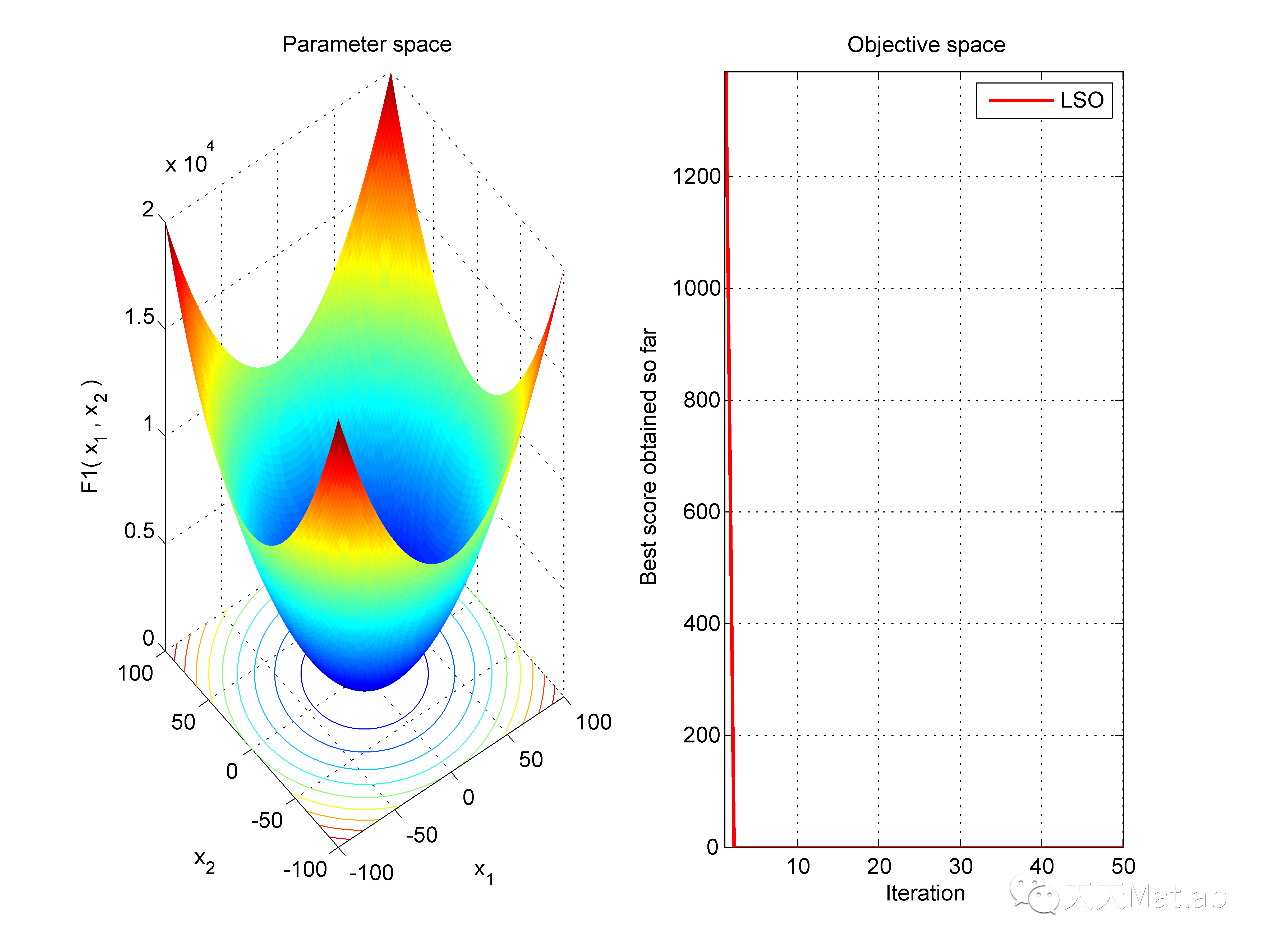
func_plot(Function_name);
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])%Draw objective space
subplot(1,2,2);
plot(LSO_curve,'Color','r','linewidth',1.5)
title('Objective space')
xlabel('Iteration');
ylabel('Best score obtained so far');axis tight
grid on
box on
legend('LSO')display(['The best solution obtained by LSO is : ', num2str(Best_pos)]);
display(['The best optimal value of the objective funciton found by LSO is : ', num2str(Best_score)]);img =gcf;  %获取当前画图的句柄
print(img, '-dpng', '-r600', './运行结果2.png')         %即可得到对应格式和期望dpi的图像    

3 仿真结果

4 参考文献

[1]杨艳, 刘生建, and 周永权. "贪心二进制狮群优化算法求解多维背包问题." 计算机应用 5(2020):1291-1294.