本文主要是介绍SGD、BGD以及负梯度，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
梯度下降举例子推导过程
https://www.jianshu.com/p/c7e642877b0e
是loss函数，对上一级的输入
求导（可以是单变量的，也可以的是多变量的），然后输出
是输入
减去梯度
减去（负号）是因为求导是梯度上升最快的方向，减去就是下降最快的方向
一、梯度下降
对噪声数据的拟合函数
与真实值y之间的误差
（1）将J(theta)对theta求偏导，得到每个theta对应的的梯度
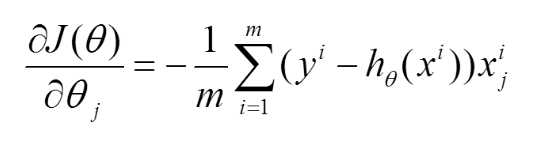
（2）由于是要最小化风险函数，所以按每个参数theta的梯度负方向，来更新每个theta
当上式收敛时则退出迭代（何为收敛，即前后两次迭代的值不再发生变化了）。一般情况下，会设置一个具体的参数，当前后两次迭代差值小于该参数时候结束迭代。注意以下几点：
(1) a 即learning rate，决定的下降步伐，如果太小，则找到函数最小值的速度就很慢，如果太大，则可能会出现overshoot the minimum的现象；
(2) 初始点不同，获得的最小值也不同，因此梯度下降求得的只是局部最小值；
(3) 越接近最小值时，下降速度越慢；
1、批量梯度下降BGD(batch gradient descent)：
批量梯度下降每次学习都使用整个训练集，
优点:每次更新都会朝着正确的方向进行，最后能够保证收敛于极值点(凸函数收敛于全局极值点，非凸函数可能会收敛于局部极值点)
缺点:每次学习时间过长，每更新一次θ值，都要用到训练集所有的数据，如果m很大，那么迭代速度就会非常慢；并且如果训练集很大以至于需要消耗大量的内存，并且全量梯度下降不能进行在线模型参数更新。
因为批量梯度下降会有很多计算冗余，因此引入了随机梯度下降。
2、随机梯度下降SGD（Stochastic gradient descent）
一样的求解公式，但是随机梯度下降每次只取一个样本来更新模型参数，因此速度非常快，可以完成在线更新，但是因为只取一个样本，随机梯度下降的方向不一定是正确的，因此会带来扰动。
图1.随机梯度下降的震荡
但扰动也不全是坏处，它的好处在于对于类似盆地区域（即很多局部极小值点）那么这个波动的特点可能会使得优化的方向从当前的局部极小值点跳到另一个更好的局部极小值点，这样便可能对于非凸函数，最终收敛于一个较好的局部极值点，甚至全局极值点。
由于波动，因此会使得迭代次数（学习次数）增多，即收敛速度变慢。不过最终其会和全量梯度下降算法一样，具有相同的收敛性，即凸函数收敛于全局极值点，非凸损失函数收敛于局部极值点。
3.小批量梯度下降mini-batch GD
小批量梯度下降是批量梯度和随机梯度下降的中和，在迭代次数和迭代速度之间做了一个折衷，每次从总样本中抽取m个（m<n），然后做批量梯度下降。理论上说batch_size越大越容易达到全局最优，一般设置在【50，256】之间，具体需要根据网络尝试。
4、对于上面的linear regression问题，与批量梯度下降对比，随机梯度下降求解的会是最优解吗？
（1）批量梯度下降---最小化所有训练样本的损失函数，使得最终求解的是全局的最优解，即求解的参数是使得风险函数最小。
（2）随机梯度下降---最小化每条样本的损失函数，虽然不是每次迭代得到的损失函数都向着全局最优方向， 但是大的整体的方向是向全局最优解的，最终的结果往往是在全局最优解附近。
如果模型只有一个peak，会收敛到全局最优解，但是往往会有multi-modal，因此得到的是局部最优解，但是一般工程而言，局部最优解的答案已经够用。
5、为什么说负梯度方向是梯度下降最快的方向？
A、B都是向量，向量点乘公式：A⋅B=||A||⋅||B||⋅cos(α)
梯度与切向量不同，例如y=x^2，切向量是y对x求偏导得到的
梯度要写成f(x,y)=x^2-y，梯度是f(x,y）对x,y都求偏导
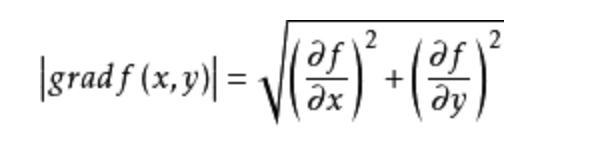
导数最大的方向就是在梯度方向，反之在负梯度方向导数最小
5.学习率的设计
（1）合适的学习率
如果学习速率过小，则会导致收敛速度很慢。如果学习速率过大，那么其会阻碍收敛，即在极值点附近会振荡。
（2）学习速率调整(Learning rate schedules）
在每次更新过程中，改变学习速率，如退火。一般使用某种事先设定的策略或者在每次迭代中衰减一个较小的阈值。
如果数据特征是稀疏的或者每个特征有着不同的取值统计特征与空间，那么便不能在每次更新中每个参数使用相同的学习速率，那些很少出现的特征应该使用一个相对较大的学习速率。
6.动量Momentum
借鉴了物理上动量的概念，积累之前的动量来替代 真正的梯度。
特点：
- 下降初期时，使用上一次参数更新，下降方向一致，乘上较大的
能够进行很好的加速
- 下降中后期时，在局部最小值来回震荡的时候，
，
- 在梯度改变方向的时候，
总结:在更新模型参数时，对于那些当前的梯度方向与上一次梯度方向相同的参数，那么进行加强，即这些方向上更快了；对于那些当前的梯度方向与上一次梯度方向不同的参数，那么进行削减，即这些方向上减慢了。因此可以获得更快的收敛速度与减少振荡。
7.比较各种优化方法
图2.SGD各优化方法在损失曲面上的表现
从上图可以看出， Adagrad、Adadelta与RMSprop在损失曲面上能够立即转移到正确的移动方向上达到快速的收敛。而Momentum 与NAG会导致偏离(off-track)。同时NAG能够在偏离之后快速修正其路线，因为其根据梯度修正来提高响应性。
图3.SGD各优化方法在损失曲面鞍点处上的表现
从上图可以看出，在鞍点（saddle points）处(即某些维度上梯度为零，某些维度上梯度不为零)，SGD、Momentum与NAG一直在鞍点梯度为零的方向上振荡，很难打破鞍点位置的对称性；Adagrad、RMSprop与Adadelta能够很快地向梯度不为零的方向上转移。
从上面两幅图可以看出，自适应学习速率方法(Adagrad、Adadelta、RMSprop与Adam)在这些场景下具有更好的收敛速度与收敛性。
重点参考（写的非常详细，非常好，受益很多）：http://www.sohu.com/a/131923387_473283
阅读：
参考：https://blog.csdn.net/lilyth_lilyth/article/details/8973972
参考：https://www.jianshu.com/p/0412e8d7b55d
参考：https://blog.csdn.net/red_stone1/article/details/80212814
这篇关于SGD、BGD以及负梯度的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
