本文主要是介绍计算机图形学Viewing视图变换理论和公式推导,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Viewing变换总结(Model+View+Projection+ViewPort)
文章目录
- Viewing变换总结(Model+View+Projection+ViewPort)
- 基本变换过程和理论
- Model transformation 模型变换
- View/Camera transformation 摄像机变换
- Projection transformation 投影变换
- 正交投影变换 Orthographic Projection Transformation
- 透视投影变换 Perspective Projection Transformation
- ViewPort transformation 视口变换
- 变换矩阵的证明过程
- ModelView变换公式推导
- 正交投影变换公式推导
- 透视投影变换公式推导
- 视口变换矩阵公式推导
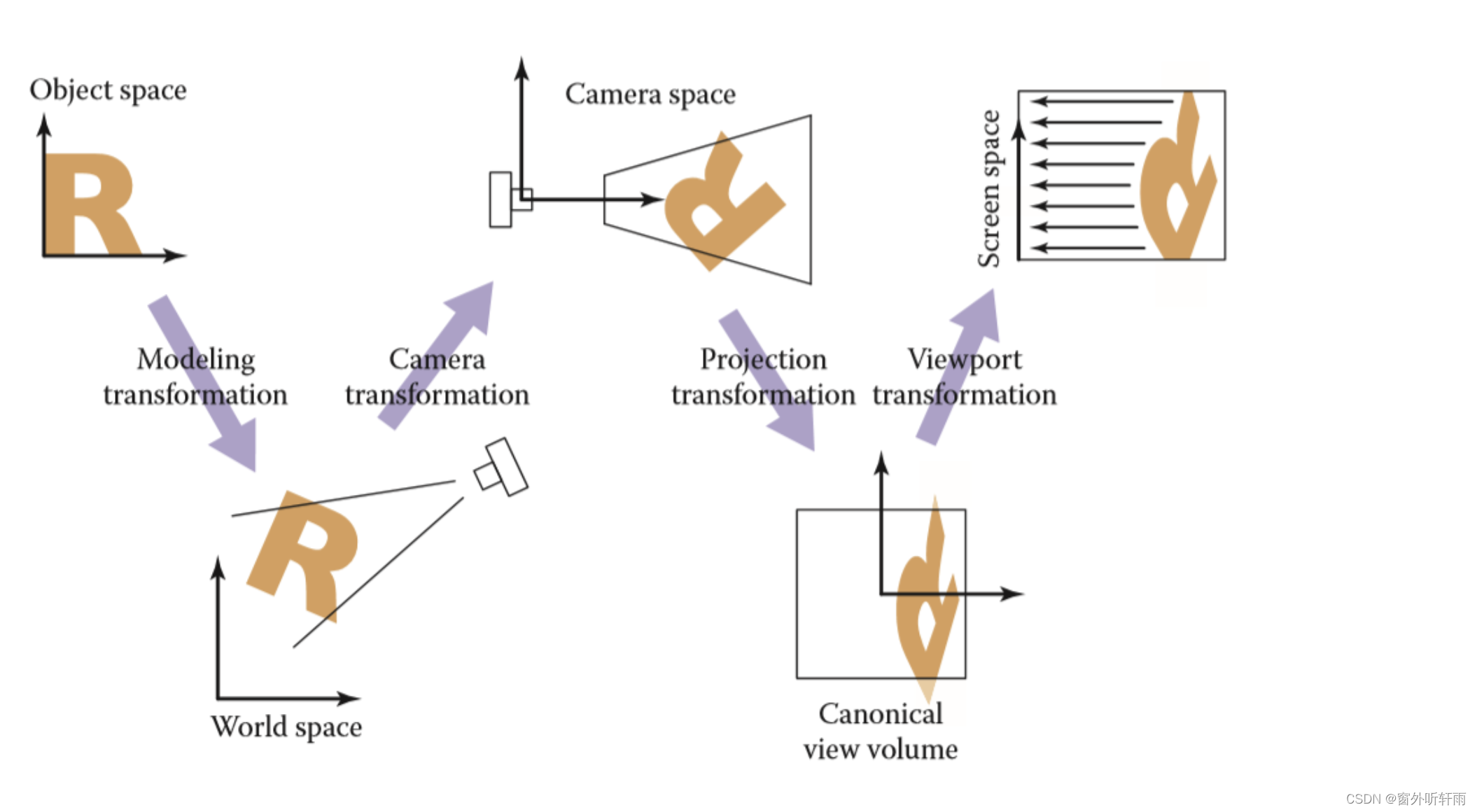
基本变换过程和理论
Model transformation 模型变换
模型和摄像机的相对位置在变换时要保持一致,在实际操作中需要对两者进行相同的变换,在摄像机变换中会进行介绍
View/Camera transformation 摄像机变换
- 原位置e(Xe,Ye,Ze,0)T 变换到原点(0,0,0,0)T
- 原朝向g(Xg,Yg,Zg,1)T 变换到-z轴方向(0,0,-1,1)T
- 原向上方向t(Xt,Yt,Zt,1)T 变换到y轴方向(0,1,0,1)T
- 原X方向g×t(Xg×t,Yg×t,Zg×t,1)T 变换到x轴方向(1,0,0,1)T
变换过程
- 先将相机移动到原点位置Tview位移变换矩阵
- 再将相机的三个轴向分别转换为x y -z轴方向
- 技巧性,将任意轴转换到标准的xyz方向不容易,但将标准的xyz方向转到任意轴相对容易。而此过程正好是互逆的,可以通过求原转换的逆矩阵,再转换回去简单的求解。
- 而且旋转矩阵还是正交矩阵,即矩阵的逆等于矩阵的转置,更加方便求解。
变换矩阵公式
Mview = Rview Tview
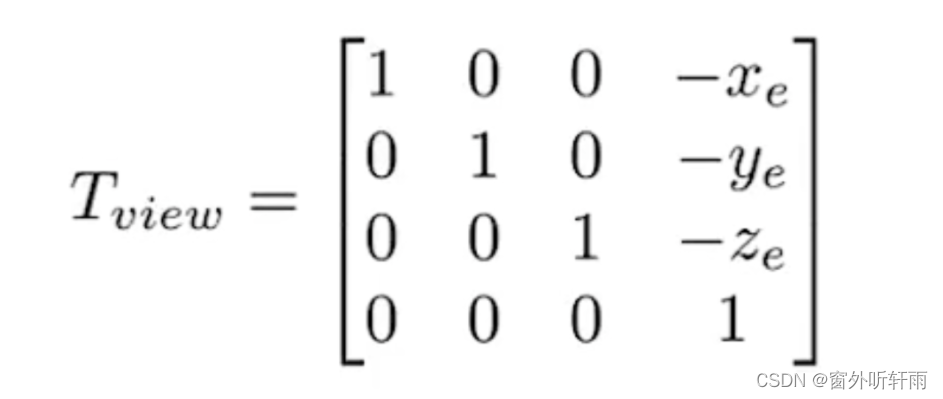
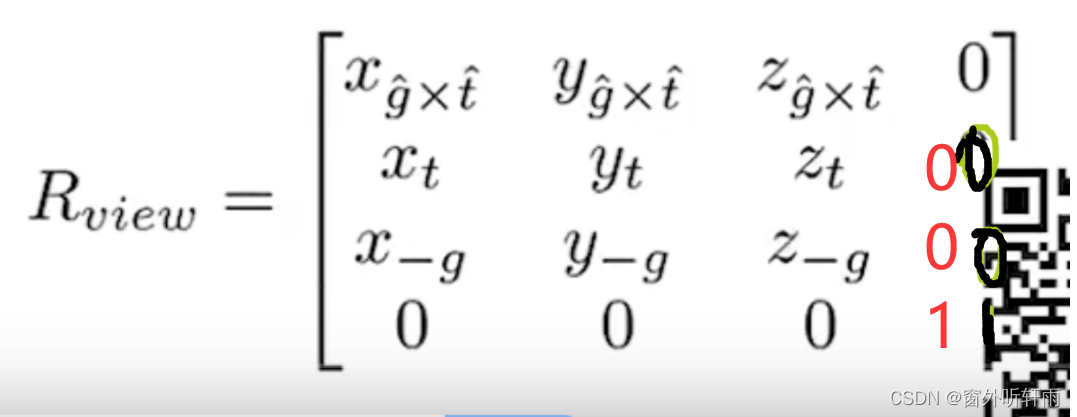
一般情况下,Model和Camera都要一并一齐转换,而Camera的目标位置和方向其实已经明确,直接就可以进行赋值而不用乘以相关转换矩阵,只需要对Model乘以此转换矩阵(因为Model的目标位置并不明确)
所以一般以上两步转换都是一块的,称作ModelView变换
Projection transformation 投影变换
正交投影变换 Orthographic Projection Transformation
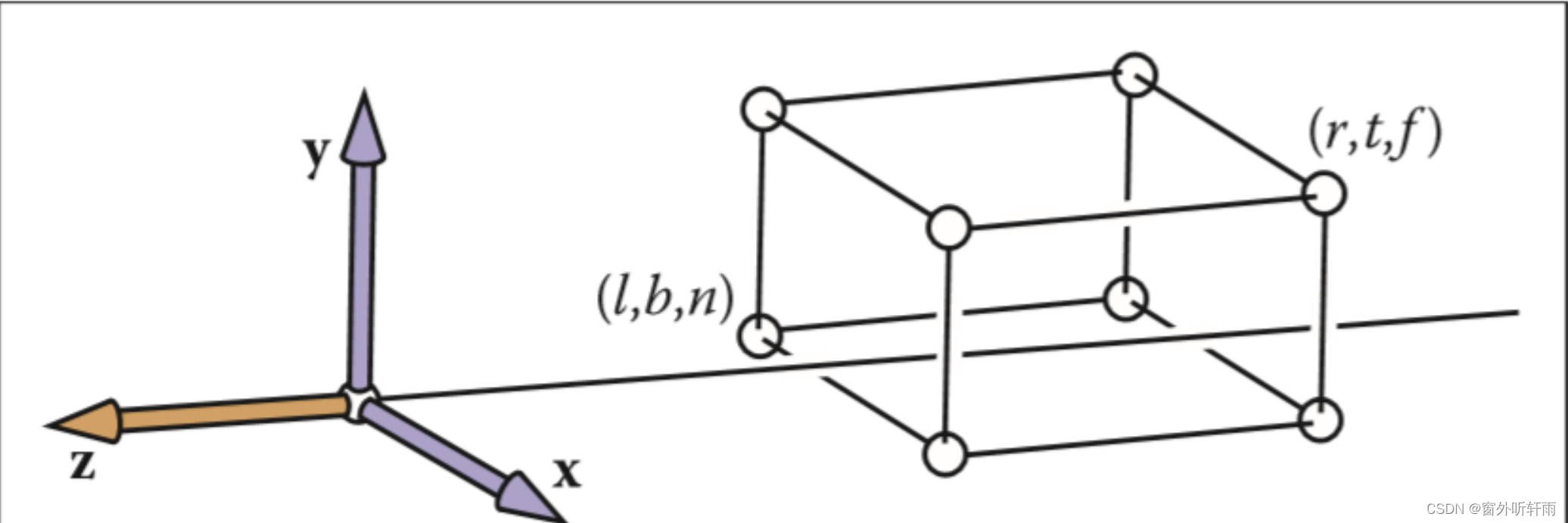
经过ModelView变换后,可以得到上图的情况,Model处于任意位置。
正交投影变换是为了将Model转换到以原点为中心的各个轴的范围都是[-1,1]长度为2的canonical cube(标准正方体中)
转换过程如下图所示 X:Left,Right Y:Top,Bottom,Z:front,Back
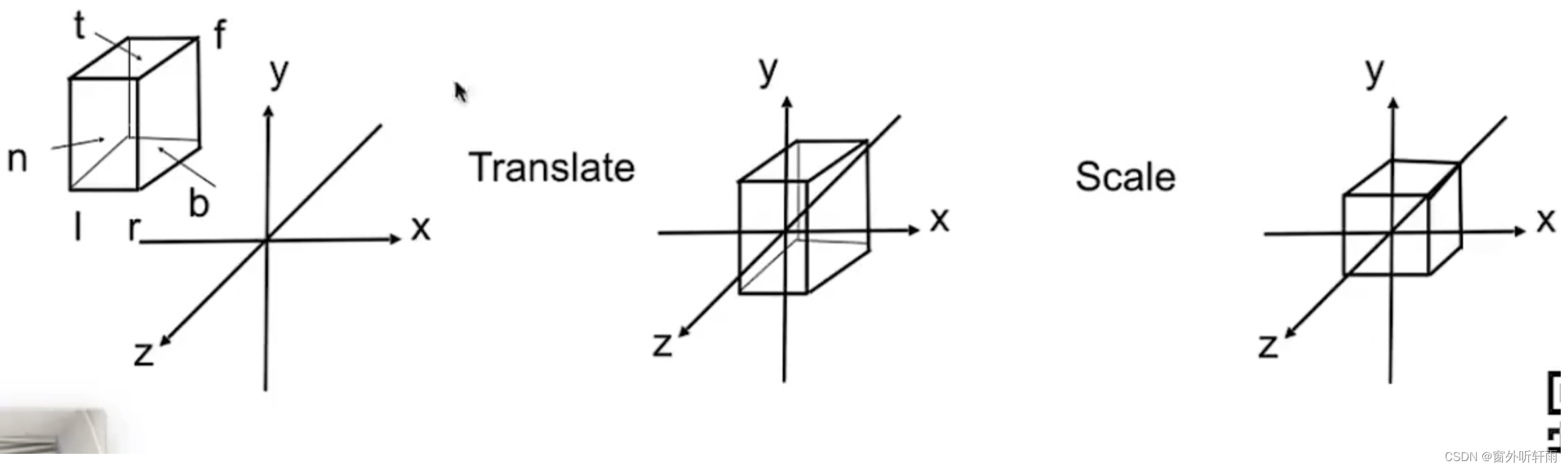
- 将Model的中心( (l+r)/2 , (t+b)/2 , (n+f)/2 , 0)T 平移到原点位置(0,0,0,0)T
- 将Model缩放(拉伸)到每个轴都是[-1,1]的范围内
注意这里是先位移再进行线性变换缩放,不能将变换矩阵合并
变换矩阵公式如下
Mortho = Sorthor Tortho

透视投影变换 Perspective Projection Transformation
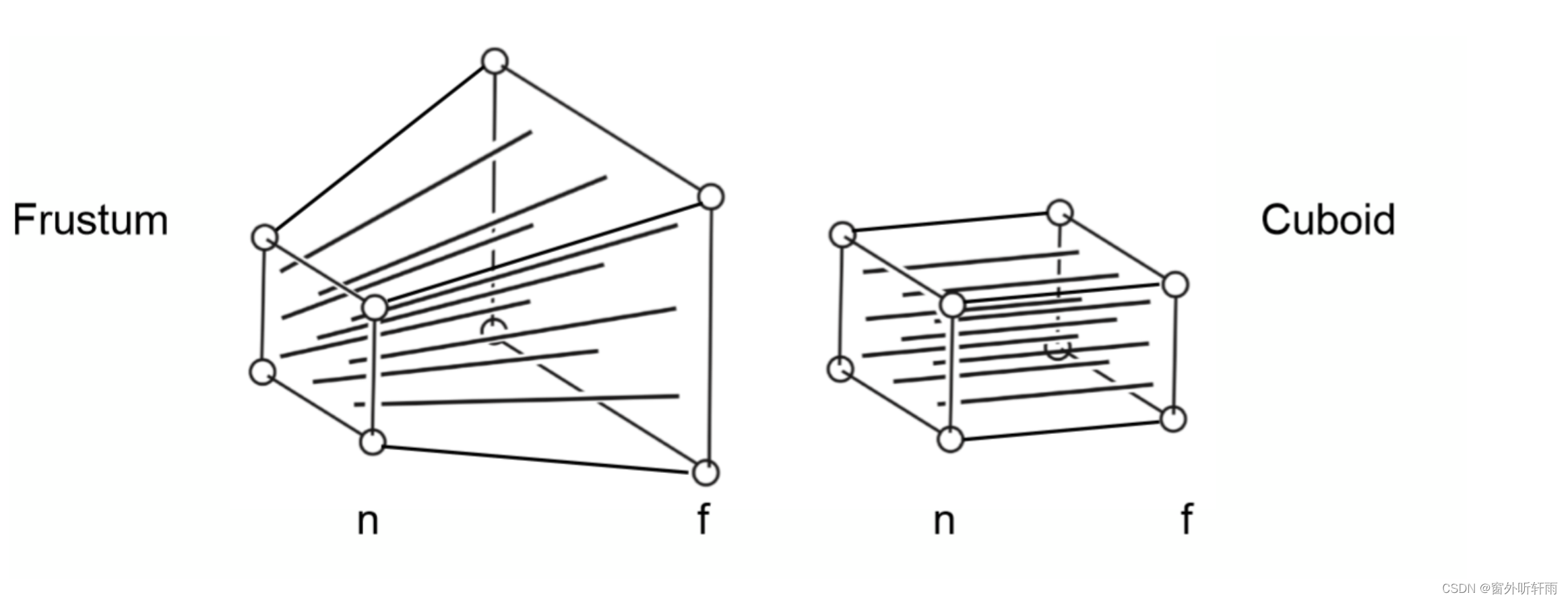
Mpersp = Mortho Mfrustum->cuboid
投影变换其实就是先将Frustum压缩成Cuboid后在进行一次正交投影变换的过程 这里主要介绍一下压缩的变换过程和公式推导
y坐标的变换
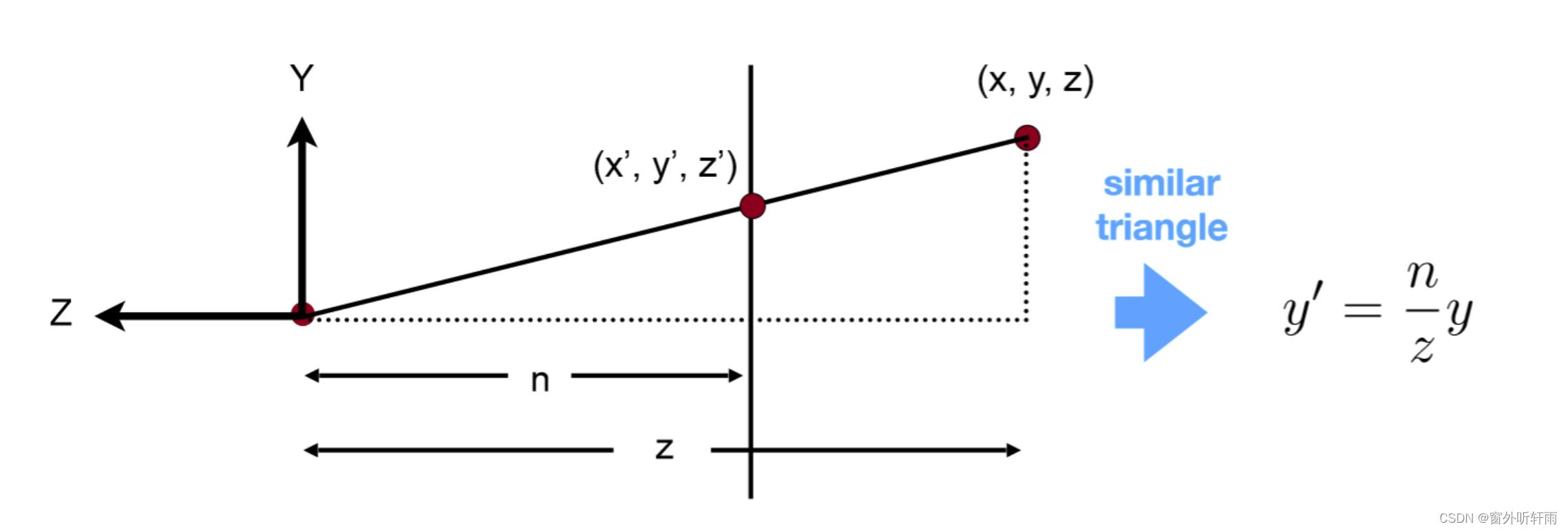
从侧面望去,利用相似三角形的性质即可求出y到y’的转换公示
x坐标的变换
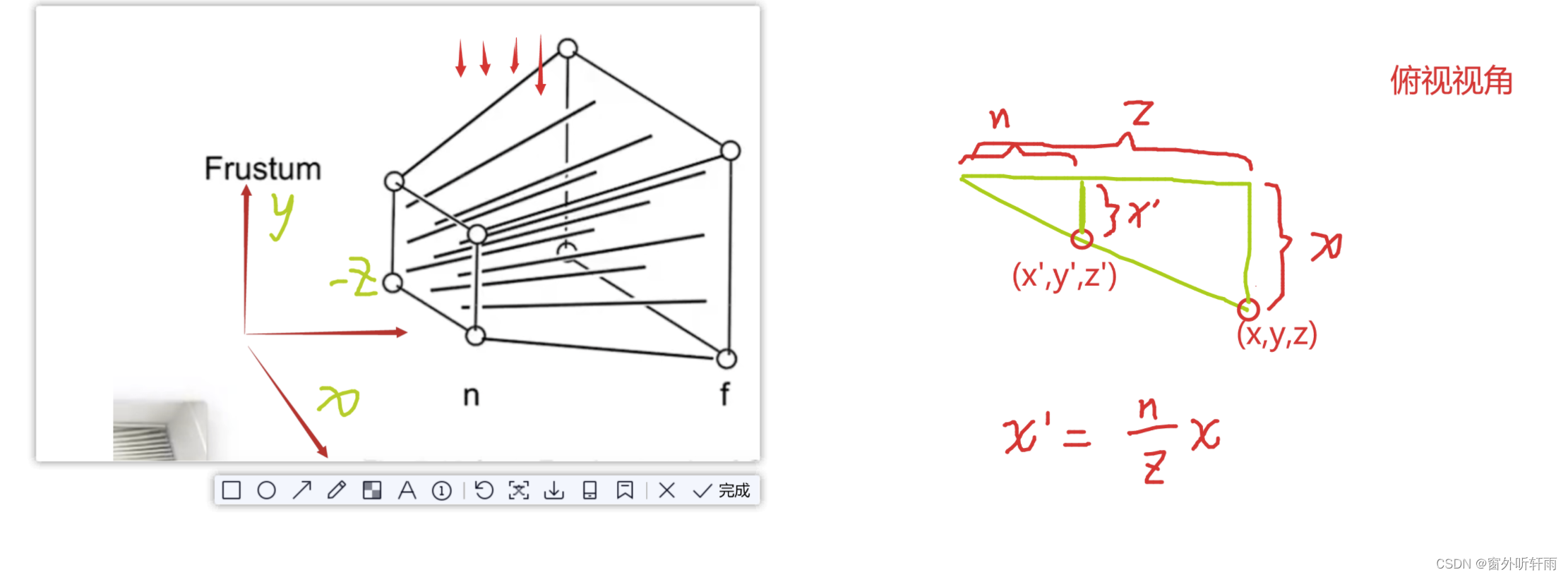
从上向下俯视望去,和y坐标同理可得x到x’的转换公式
z坐标的转换
根据x和y已经能求出绝大部分的矩阵的元素,但是关于z的转换的那一列仍是未知的,主要思路为根据几个特性代入特殊值求解。
- 近平面(z=n)的所有坐标在转换前后,位置坐标不变
- 远平面的中心点(z=f,x=y=0)在转换后,位置坐标不变
根据以上两个特效即可求出最终的结果,具体证明过程参考后面
变换公式
压缩矩阵 Mfrustum->cuboid如下
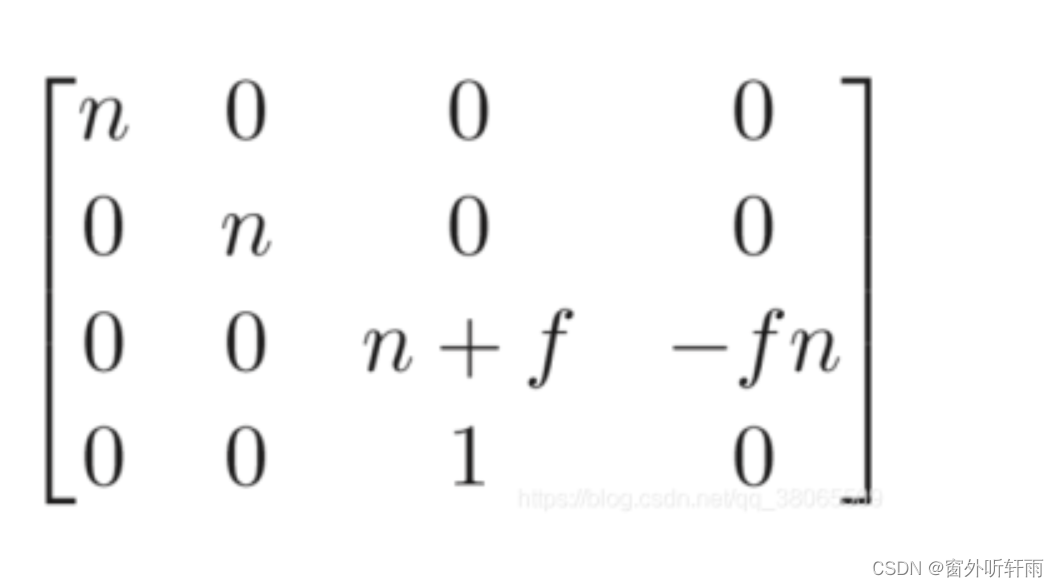
Mper = MorthoMpersp->ortho

投影变换矩阵结果公式结果如上图
ViewPort transformation 视口变换
视口变换是为了将原标准立方体,忽略z轴并变换到屏幕空间,即原来的x和y的范围[-1,1]变换成x:[0,width] y:[0,height]
变换过程
- 忽略z轴
- 先将原标准[-1,1]立方体拉伸至[-width/2,width/2] [-height/2,height/2]
- 然后将立方体的左下角(-width/2,-height/2)移动到原点处(为了和屏幕空间坐标系对应)
视口变换矩阵
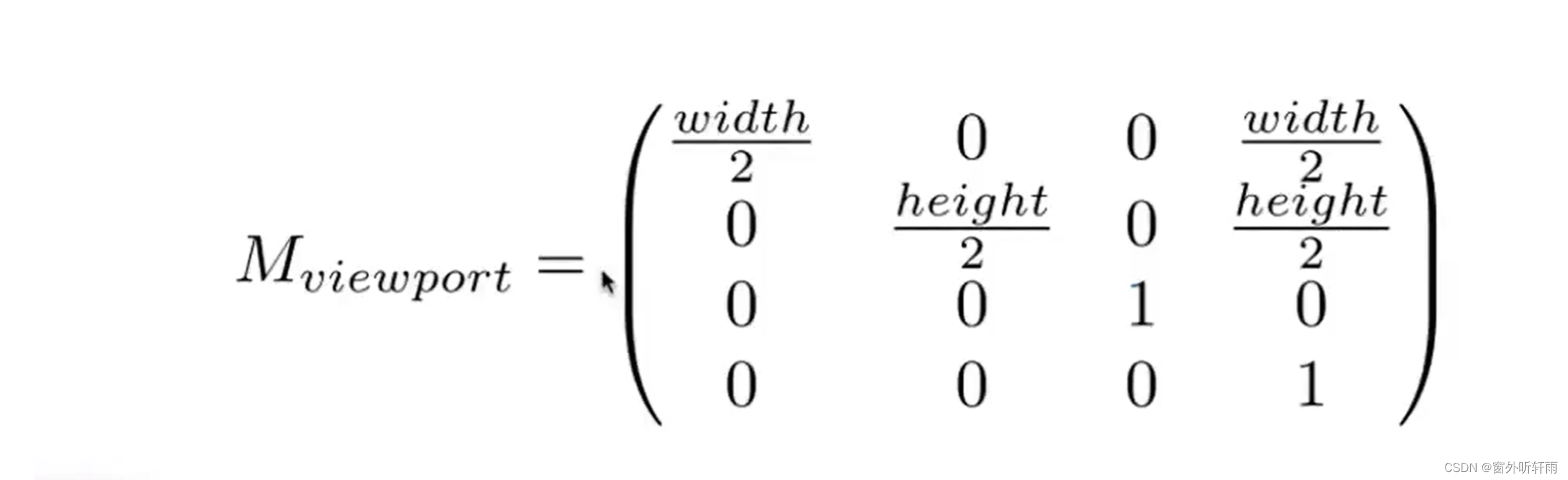
总结转换

变换矩阵的证明过程
ModelView变换公式推导

正交投影变换公式推导
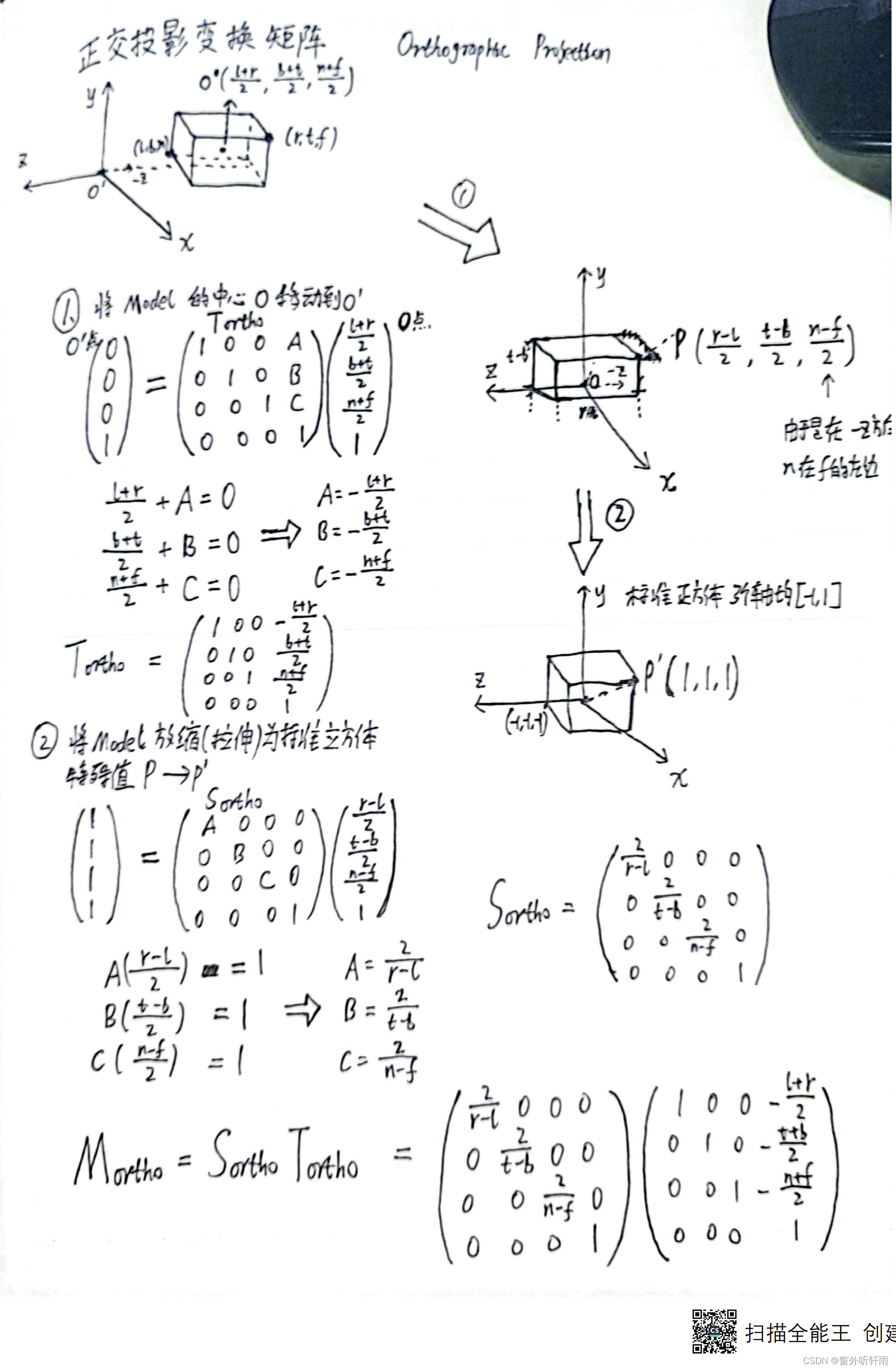
透视投影变换公式推导
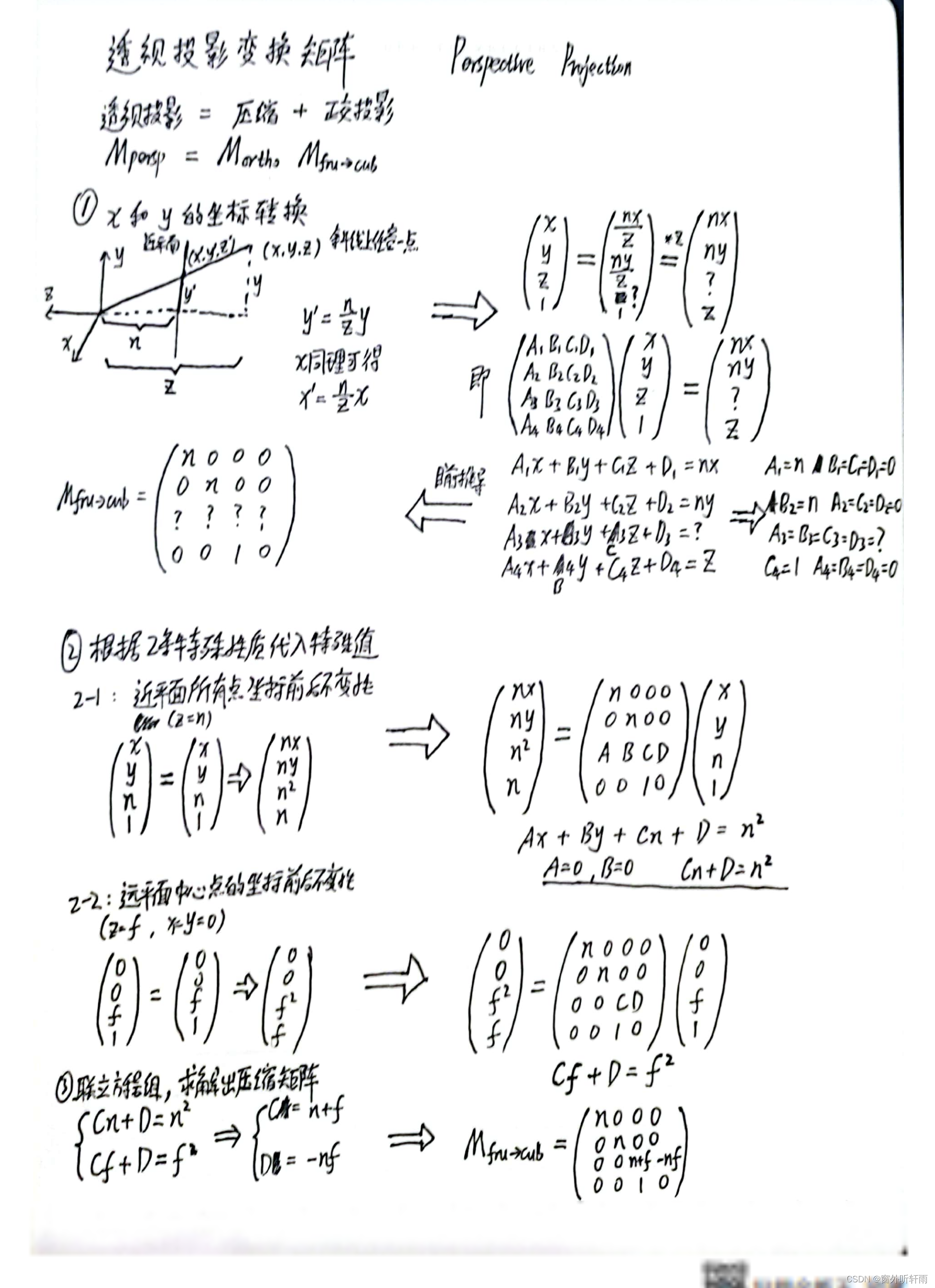
视口变换矩阵公式推导
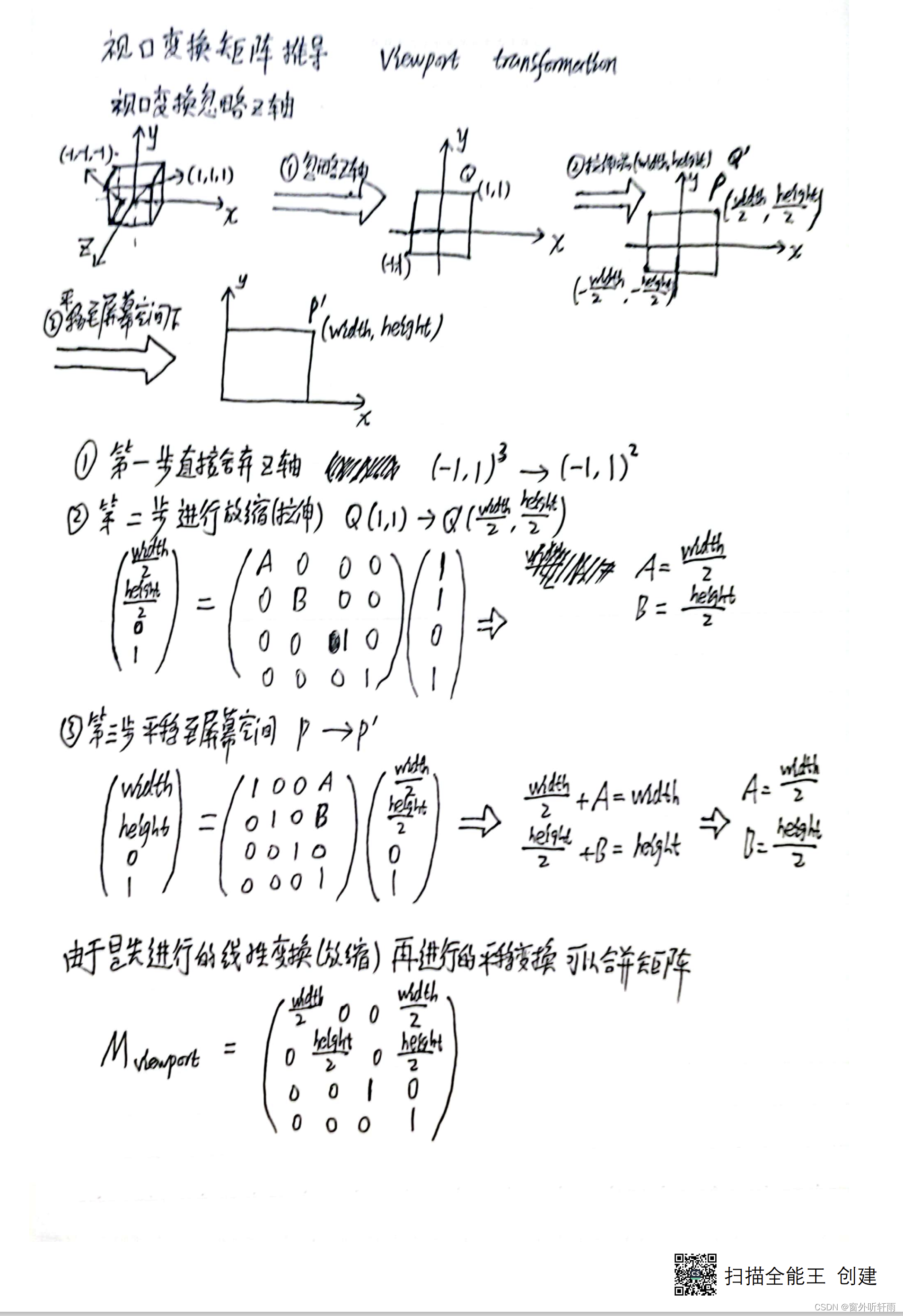
这篇关于计算机图形学Viewing视图变换理论和公式推导的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








