Lecture 3: Independence

前言：本文讲了事件之间的独立性
独立性定义
韦恩图不能表述独立性
条件对独立性的影响
独立和两两独立的关系

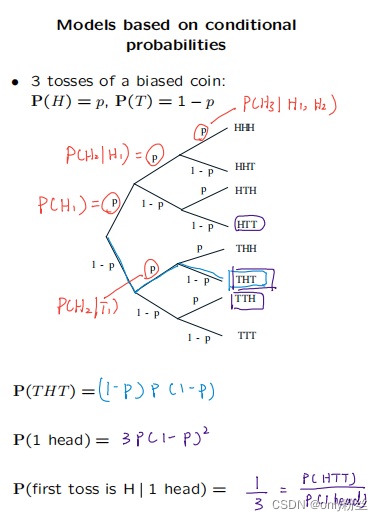
第二次掷硬币的概率不会被第一次投掷的结果所影响，都是P
independence： the first event whether or not occour, will not bring any information that affect the second event

第一种定义
A的出现不会影响任何对于B的判断。
这种定义里$P(A)$ 一定大于0， 不然条件概率没有意义
第二种定义：
两个事件AB同时发生的概率是两个事件发生概率的乘积

A 和 B完全不是独立事件，如果A 发生 B一定不发生，韦恩图不能判断事件是否独立

当被告知event C已经发生的时候，所有发生的outcome只会落在C中，所以we have a new universe, 然而在这个新的universe中，A和B是disjoint的，由上文可知，一定不是独立的。

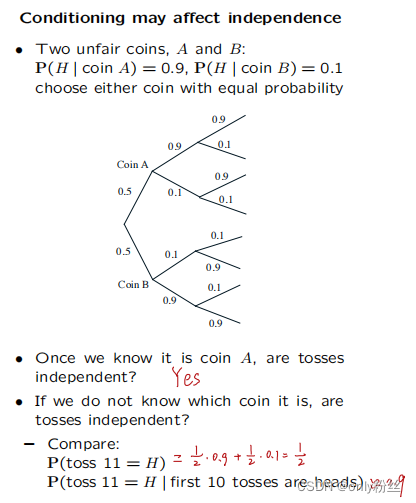
如果知道前十次都是head很大可能是coinA，所以在这个例子里，第十一次是head和前十次都是head是不独立的，是会互相影响的。

举例：
如果 n = 3
$$\begin{gathered} P(A_1\cap A_2\cap A_3)=P(A_1)P(A_2)P(A_3) \\ P(A_1\cap A_2)=P(A_1)P(A_2) \\ P(A_1\cap A_3)=P(A_1)P(A_3) \\ P(A_2\cap A_3)=P(A_2)P(A_3) \end{gathered}$$
上面这个就是3个事件完全独立。
还有一种独立是两两独立（pairwise independence），和完全的独立是不一样的，对于上面的例子$P(A_1\cap A_2\cap A_3)=P(A_1)P(A_2)P(A_3)$这个条件不是trivial的

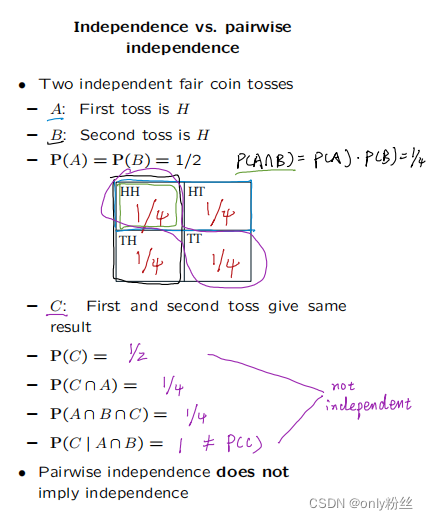
这个例子里：A发生没有对C产生影响，B发生没有对C产生影响，但是AB同时发生就会对C产生影响。

moral: 寓意
impose a requirement
precedence：领先; 优先权; 地位先后