本文主要是介绍【计算机视觉】Lecture 16：平面单应变换，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
动机：在平面上的点
回顾：正向投影
世界坐标系到相机坐标系的变换
透视矩阵方程（相机坐标系到成像坐标系）
成像坐标系到像素坐标系
从成像坐标（x，y）到像素坐标（u，v）的二维仿射变换Maff
平面上点的投影
单应性矩阵H（平面投影变换）
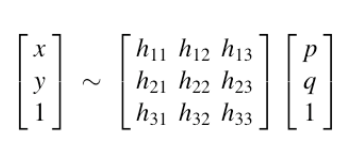
单应性矩阵H（平面投影变换）
对于平面，3D到2D的透视投影降为2D到2D的变换。，并且此变换是可逆的
特殊情况：正平面
如果平面垂直于光轴（相机坐标系的Z轴），怎么办？
世界坐标系旋转矩阵简化为：
所以正平面的单应性简化为：
是一个相似变换
转换到像素坐标系
平面投影图
总结：平面投影
应用单应性变换去除透视畸变
针对平面建筑面，4组匹配点对足以
鸟瞰图的单应性变换
图像拼接的单应性变换
两个实际问题
-
给定四个或更多匹配点对，如何估计对应的单应性矩阵（将会用最小二乘法推导）
-
如何（反向）映射图像像素值以生成新图片（上一节课讲的）
估计单应性矩阵
矩阵形式：
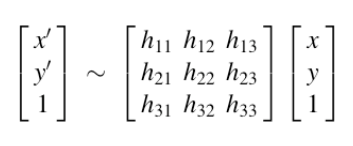
方程形式：
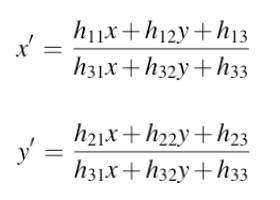
自由度？
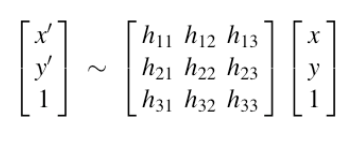
这里有有个变量 h11，…，h33，所以自由度是9？
并不是。
注意，我们可以将所有 hij 乘以非零常数 k，而不必改变方程组
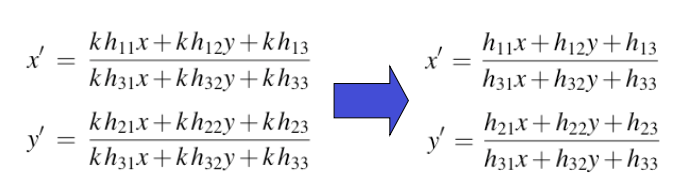
采用8自由度
一种方法：设 h33 = 1
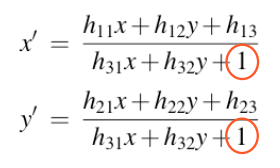
第二方法：增加单位向量约束
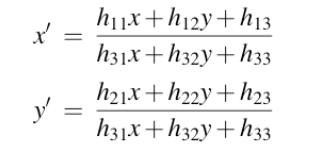
单位向量约束：
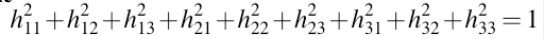
代数距离的最小二乘
设 h33 = 1 ：
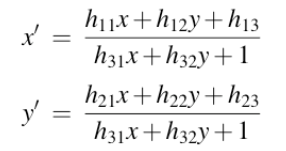
乘以分母：
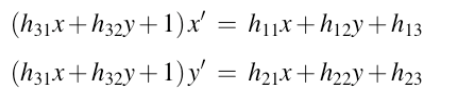
整理：
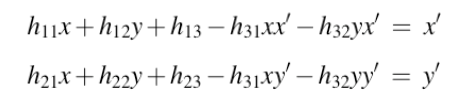
线性方程：
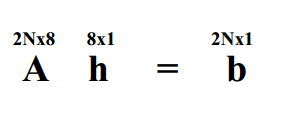
解：
Matlab：
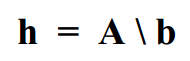
注意：数值调节
R.Hartley: “In Defense of the Eight Point Algorithm”
八点法Eight Point Algorithm
观察：根据点对应关系对射影变换参数进行线性估计时，常常会遇到矩阵条件差（poor “conditioning” ）的问题。这意味着这样的解法对对应点的噪声敏感（即使没有外点）。
为了得到更好的答案，通过对每个点集进行规范化来对矩阵进行预处理，方法是：
- 将点集质心平移为原点
- 缩放，使点集与原点的平均距离为sqrt（2）。
- 对每个点集独立进行标准化
Hartley的预处理
更一般的方法
设 h33 = 1 可能会产生什么问题？
如果 h33 实际上等于0，我们就不能得到正确的答案。
代数距离，||h||=1
||h||=1：
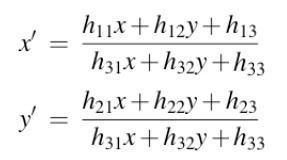
乘以分母：
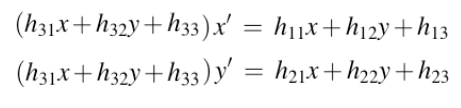
整理：
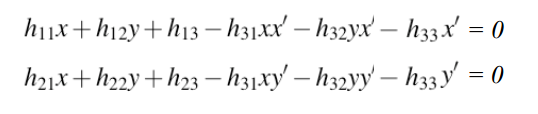
齐次方程：
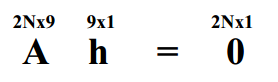
解：
设 h 为与矩阵 D 中最小特征值相关联的矩阵 U 的列（也就是单位特征向量）
（注：如果只有4个点，则该特征值为0）
这篇关于【计算机视觉】Lecture 16：平面单应变换的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
