本文主要是介绍【计算机视觉】Lecture 19:本质矩阵和基础矩阵,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
对极几何

左边
极点:相机1所看到的相机2的位置。
右边
极点:相机2所看到的相机1的位置
对极几何

对应点位于共轭极线上
对极几何

给定一幅图像中的一个点,我们如何确定在第二幅图像中要搜索的对应极线?
本质矩阵Essential Matrix
本质矩阵和基础矩阵都是 3x3 的矩阵,用于“编码”两个视图的对极几何。
动机:给定一张图像中的一个点,乘以本质/基础矩阵将告诉我们在第二个视图中沿着哪个极线搜索。
本质矩阵

R,T是旋转和平移
S是平移T的反对称矩阵
E = RS,称为本质矩阵
本质矩阵性质

- rank为2,有左和右零空间(nullspace)
- 仅取决于外参(R和T)
Longuet-Higgins方程

 上式和观察射线(相机坐标系坐标)相关
上式和观察射线(相机坐标系坐标)相关
下式和二维成像(成像平面上)点有关
Longuet-Higgins意义
成像点也可以被认为是射线。 它们是等价的。
(u, v)二维成像点
(u, v, f)成像平面上的三维点
k(u, v, f )进入场景的观察射线
k(X, Y, Z)通过场景中点P的射线
注意:k = f / Z,并且u=fX/Z, v=fY/Z
极线
l为图像中的一条直线:
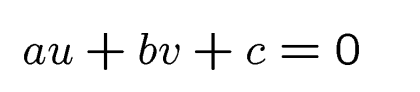
使用齐次坐标:
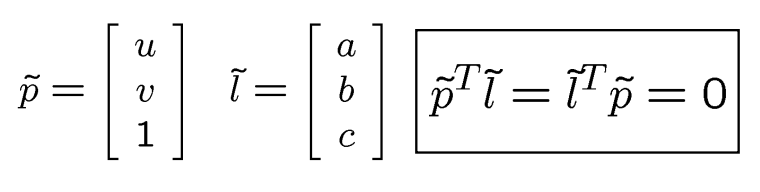
记住:
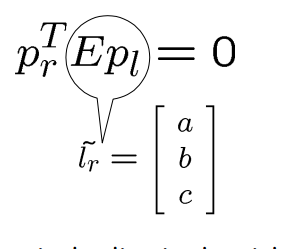
对于pr,右图像中的极线被定义为:
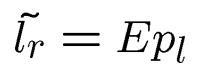
记住:
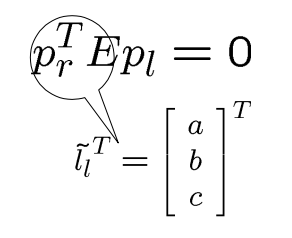
对于pl,左图像中的极线被定义为:
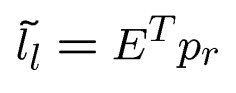
极点
记住:极点属于极线
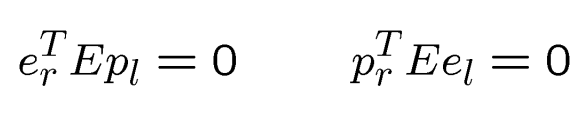
它们属于所有的极线
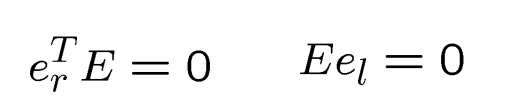
这可以用来计算极点的位置
本质矩阵总结
Longuet-Higgins方程
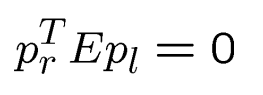
极线:
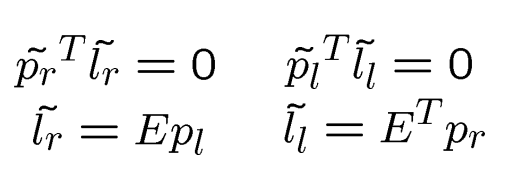
极点:
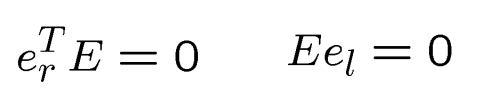
基础矩阵Fundamental Matrix
本质矩阵(essential matrix)是使用相机坐标(或者成像坐标)
为了使用图像(像素)坐标,我们必须考虑相机内参


简而言之:总结中的方程也同样适用于像素坐标!
基础矩阵性质
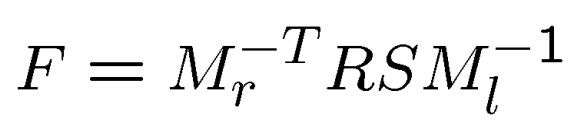
-
rank为2
-
取决于内参和外参(内参:f,偏移ox,oy,尺度s;外参:R和T)
类似于本质矩阵。基础矩阵也说明了每个图像中的像素(点)如何与另一个图像中的极线相关。
例子


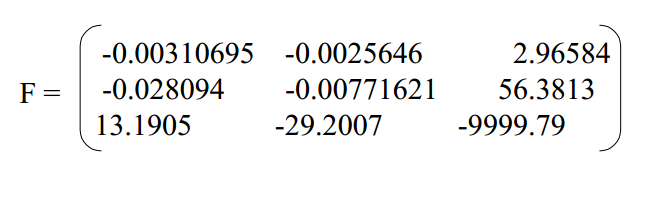

归一化,使前两项的平方和为1(可选)



左极点在哪里?

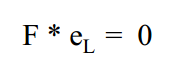
矩阵 F 的右零空间中的向量
但是,由于噪声的存在,F可能不是奇异的。
因此,这种情况最好的就是与F的最小特征值相关的特征向量

右极点在哪里?

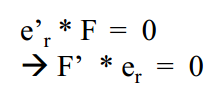
矩阵 F’ 的右零空间中的向量
但是,由于噪声的存在,F’ 可能不是奇异的。
因此,这种情况最好的就是与 F’ 的最小特征值相关的特征向量

这篇关于【计算机视觉】Lecture 19:本质矩阵和基础矩阵的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






