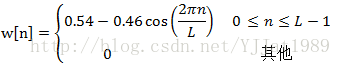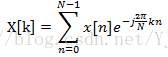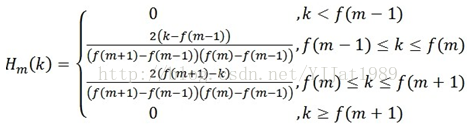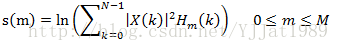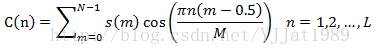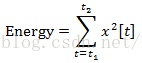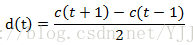本文主要是介绍声音特征提取:MFCC向量,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
模数转换就是把模拟信号转换为数字信号,包括两个步骤:采样和量化,即以一定的采样率和采样位数把声音连续波形转换为离散的数据点。由于日常生活中的声音一般都在8kHz以下,根据Nyquist定律,16kHz采样率足以使得采样出来的数据包含大多数声音信息。16kHz意味着1s的时间内采样16k个样本,这些样本都是以幅度值存储,为了有效存储幅度值,需要将其量化为整数。对于16位采样位数来说,可以表示-32768~32767之间的整数值,所以可以将采样幅度值量化为最近的整数值。
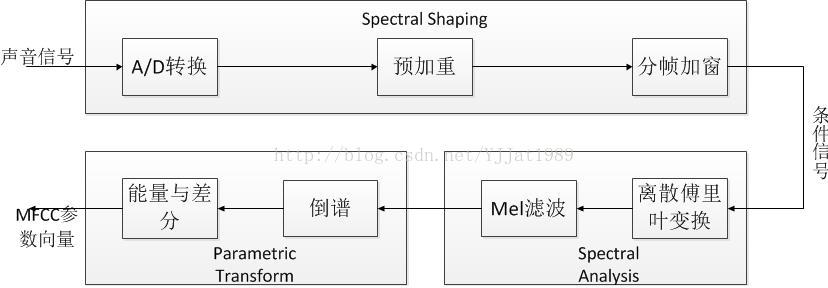
采样和量化后的波形表示为x[n],其中n是时间索引。然后可以对x[n]做MFCC特征提取,算法流程图如图:
一、预加重
MFCC特征提取的第一步是增加声音高频部分的能量。对于声音信号的频谱来说,往往低频部分的能量高于高频部分的能量,每经过10倍Hz,频谱能量就会衰减20dB,而且由于麦克风在采集声音信号时电路本底噪声的影响,也会增加低频部分的能量,为使高频部分的能量和低频部分能量有相似的幅度,需要预加强采集到声音的高频能量。加强高频部分的能量能使声学模型更好的利用高频共振峰,从而提高识别准确率。
预加重可以通过一个一阶高通滤波器实现,在时域,如果输入信号是x[n]并且0.9<=a<=1.0,滤波器表示为y[n]=x[n]-ax[n-1];在频域则表示为H(z)=1-a*z-1。
二、加窗
日常生活中的声音一般是非平稳信号,其统计特性不是固定不变的,但在一段相当短的时间内,可以认为信号时平稳的,这就是加窗。窗由三个参数来描述:窗长(单位毫秒)、偏移和形状。每一个加窗的声音信号叫做一帧,每一帧的毫秒数叫做帧长,相邻两帧左边界的距离叫帧移。
从信号s[n]中提取一帧的过程可表示为y[n]=w[n]s[n],如果w[n]是矩形窗,则信号会在边界处切断,这些不连续会对傅里叶分析造成影响。因此在MFCC中,加窗一般使用边缘平滑降到0的汉明窗,表达式如下:
其中L为帧长。
三、离散傅里叶变换
在得到加窗的每一帧信号后,需要知道此帧信号在不同频段的能量分布。从一个离散信号(采样信号)中提取离散频段频谱信息的工具就是离散傅里叶变换(DFT)。DFT的输入是一帧帧加窗后的信号x[n]…x[m],输出则是包含N个频带的复数X[k],表示原始信号中某一频率成分的幅度和相位。DFT的定义如下:
计算DFT常用的一个算法是快速傅里叶变换(FFT),它非常高效但是一般要求N是2的幂。
四、 Mel滤波器组
FFT的结果包含此帧信号在每一频带的能量信息。但是,人耳听觉对不同频带的敏感度是不同的,人耳对高频不如低频敏感,这一分界线大约是1000Hz,在提取声音特征时模拟人耳听觉这一性质可以提高识别性能。在MFCC中的做法是将DFT输出的频率对应到mel刻度上。一mel是一个音高单位,在音高上感知等距的声音可以被相同数量的mel数分离[18]。频率(单位Hz)和mel刻度之间的对应关系在1000Hz以下是线性的,在1000Hz以上是对数的,其计算公式如下:

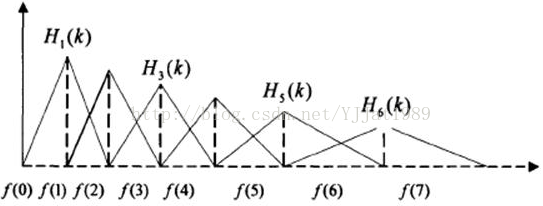
在计算MFCC时,将FFT频谱通过一组mel滤波器组就可以转换为mel频谱。Mel滤波器组一般是一组mel刻度的三角形滤波器组,1000Hz以下的10个滤波器线性相隔,1000Hz以上的剩余滤波器对数相隔。定义一个有M个滤波器的滤波器组,采用的滤波器为三角滤波器,中心频率为f(m),m=1,2,…,M,M通常取22-26(滤波器的个数和临界带个数相近)。各f(m)之间的间隔随着m值的减小而缩小,随着m值的增大而增宽,如图:
每个三角滤波器的频率响应为:
式中
使用三角带通滤波器,可以对频谱进行平滑,并消除谐波的作用,突显原始声音的共振峰。因此一段声音的音调或音高,不会反应在MFCC参数内,也就是说以MFCC作为声学特征,并不会受到输入声音的音调不同而对识别结果有所影响。此外,还可以降低运算量。
在得到mel频谱后,计算每个滤波器组输出的对数能量。一般人对声音声压的反应呈对数关系,人对高声压的细微变化敏感度不如低声压。此外,使用对数可以降低提取的特征对输入声音能量变化的敏感度,因为声音与麦克风之间的距离是变化的,因而麦克风采集到的声音能量也是变化的。每个滤波器输出的对数能量为:
五、倒谱:离散余弦变换
尽管可以用mel频谱本身作为声音特征,但使用倒谱有其优点并且可以提高识别性能。抛开预加重和mel刻度转换,倒谱的定义可以看做是频谱对数的频谱,即将标准幅度谱的幅度值先取对数,然后形象化对数谱使其看起来像声音波形。倒谱这个单词cepstrum正是将单词spectrum(频谱)的前四个字母颠倒而来,频谱是将时域信号变换为频域信号,倒谱则是将频域信号又变换回时域信号;在波形上,倒谱与频谱有相似的波形,即如果频谱在低频处有个峰值,则倒谱在低倒谱系数上也有峰值,如果频谱在高频处有个峰值,则倒谱在高倒谱系数上也有峰值。所以如果是为了检测音元,可以用低倒谱系数;如果是检测音高,则可以用高倒谱系数。倒谱系数的优点是其不同系数的变化是不相关的,意味着高斯声学模型(高斯混合模型GMM)无需表现所有MFCC特征的协方差,因而大大减少了参数数量。
利用滤波器的对数能量,倒谱系数可以由离散余弦变换获得:
式中L指MFCC阶数,通常12阶就可以代表声学特征;M指三角滤波器个数。
六、能量和差分
某一帧的能量定义为某一帧样本点的平方和,对于一个加窗信号x,其从样本点t1到样本点t2的能量为:
实际应用中也可以将上式取以10为底的对数值,再乘以10。若要加入其他声音特征如音高、过零率及共振峰等也可以在这一阶段加入。
以上提取的特征每一帧单独考虑,是静态的,而实际声音是连续的,帧与帧之间是有联系的,因而需要增加特征来表示这种帧间的动态变化,这通常通过计算每一帧13个特征(12个倒谱特征加上1个能量)的一阶差分甚至二阶差分来实现。一个简单计算差分的方法就是计算当前帧前后各一帧的13个特征的差值:
如果不考虑二阶差分,最终每一帧的MFCC特征为26维度:12维倒谱系数、12维倒谱系数差分、1维能量和1维能量差分。
这篇关于声音特征提取:MFCC向量的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!