Bresenham算法的推导和改进（适应第一象限的任意斜率任意方向）

简述

在游戏的寻路中或者射线找最远可达点经常会用到Bresenham算法。引用别人的文章来介绍一下Bresenham算法的推导过程。并会给出一个在第一象限的全方向版Bresenham算法的java版本。

原文链接 http://blog.chinaunix.net/uid-21228455-id-2406397.html

直线光栅化

直线光栅化是指用像素点来模拟直线. 比如下图中用蓝色的像素点来模拟红色的直线. 图中坐标系是显示器上的坐标系: x轴向右, y轴向下.

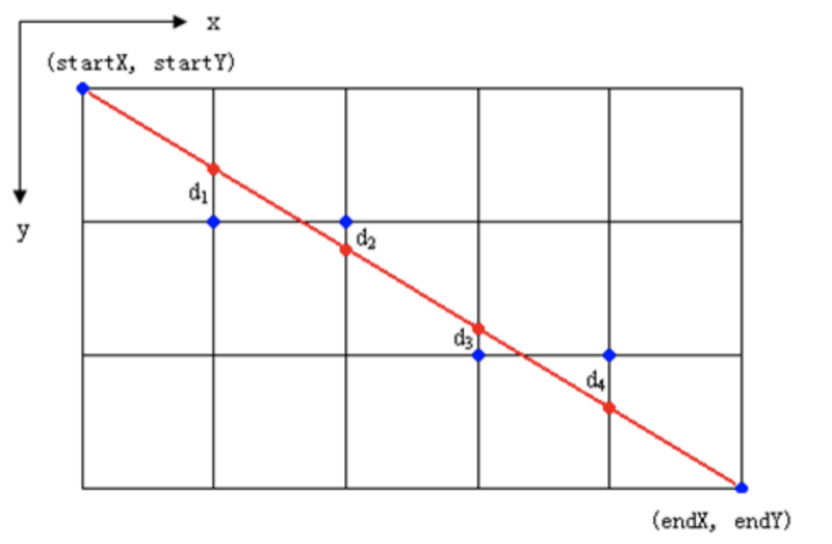
设deltaX = endX – startX, deltaY = endY – startY. 那么斜率为k = deltaY / deltaX. 我们先考虑简单的情况: 当 0 < k < 1即直线更贴近x轴. 在这种情况下deltaY < deltaX, 所以在光栅化的过程中, 在y轴上描的点比在x轴上描点少. 那么就有一个很直观的光栅化算法:

line_bresenham(startX, startY, endX, endY) {deltaX = endX - startX;deltaY = endY - startY;k = deltaY / deltaX;for (x = startX, y = startY; x <= endX; ++x) {if (满足一定条件) {++y;}drawPixel(x, y);}
}

基于斜率 / 距离的两个简单直线光栅化算法
好了，貌似很简单, 就剩一个问题: “满足一定条件”是什么? 可以用斜率判断, 也可以用上图中直线与光栅线交点 (红点) 与光栅点 (蓝点) 的距离来判断. 继续用伪代码说话:

// 算法1: 用斜率判断
void line_bresenham_k(startX, startY, endX, endY) {deltaX = endX - startX;deltaY = endY - startY;k = deltaY / deltaX;for (x = startX, y = startY; x <= endX; ++x) {if (x - startX != 0) {// 计算当前斜率currentK = (y - startY) / (x - startX);// 如果当前斜率 < k, 则增加y坐标if (currentK < k) {++y}}drawPixel(x, y);}
}

// 算法2: 用距离判断. 计算直线与光栅线交点y坐标我们需要用到
// 直线方程 y = k (x - startX) + startY
line_bresenham_dist(startX, startY, endX, endY) {deltaX = endX - startX;deltaY = endY - startY;k = deltaY / deltaX;for (x = startX, y = startY; x <= endX; ++x) {// 计算直线与光栅线交点的y坐标, 以及与光栅点的距离ptY = k * (x - startX) + startY;dist = ptY - y;// 如果距离 > 0.5或者 < -0.5, 说明我们需要增加y以// 将距离的绝对值控制在0.5之类if (dist > 0.5 || dist < -0.5) {++y;}drawPixel(x, y);}
}

消灭浮点数!

以上都是很直观的算法, 下面不直观的来了 – 上面的算法都需要在循环体内执行乘法, 准确的说, 是进行浮点数的乘法. 我们怎么能减少这些浮点数的乘法开销呢? 以基于距离的算法2为例: 首先, k是一个浮点数, 0.5也是浮点数. 我们可以通过将这些表达式都乘以2 * deltaX (整数) 来解决浮点数的问题. 伪代码:

// 算法3: 在算法2的基础上消灭浮点数!
line_bresenham_dist(startX, startY, endX, endY) {deltaX = endX - startX;deltaY = endY - startY;for (x = startX, y = startY; x <= endX; ++x) {// 计算直线与光栅线交点的y坐标, 以及与光栅点的距离ptY1 = deltaY * (x - startX) + startY * deltaX;dist1 = ptY1 - y * deltaX;dist1 = dist1 << 1; // dist1 = dist1 * 2// 如果距离 > 0.5或者 < -0.5, 说明我们需要增加y以// 将距离的绝对值控制在0.5之类if (dist1 > deltaX || dist < -deltaX) {++y;}drawPixel(x, y);}
}

消灭乘法!

圆满解决浮点数运算问题! 不过…乘法运算还在. 消灭乘法问题的办法比较不直观, 让我们想一想: 还有什么办法能简化运算. 直线方程已经不能再简化, 所以唯一的突破口就是能不能利用递推 / 用上一次循环的计算结果推导下一次循环的计算结果.
首先我们来看看在算法2的基础上 (因为算法2计算红点蓝点之间的距离, 比较直观), 怎么通过第n – 1次循环计算出的dist值 (设为d1) 来推导出第n次循环的dist值 (设为d2). 先回顾一下: dist = 直线与光栅线交点的y坐标 – 相应光栅点的y坐标. 我们从几何上直观地考虑: 在第n次循环中, 我们先根据上一次循环所计算出来的d1, 暂时令d2 = d1 + k, 因为我们要保证-0.5 < d2 < 0.5, 而d1 + k满足d1 + k > –0.5, 所以我们只需要考虑当d1 + k > 0.5时, 我们需要将光栅点y坐标增加1, 并且将d2减去1. 显然, 设y1是第n – 1次循环中光栅点的y坐标, y2是第n次循环中光栅点的y坐标. 我们有

1. d2 = d1 + k – (y2 – y1)
2. 当d1 + k > 0.5时y2 = y1 + 1, 否则y2 = y1
   我们已经能根据上面的两个关系式写出算法, 不过为了消除乘法和浮点数, 我们将这两个关系式两端同时乘以2 * deltaX, 并且设e = 2 * deltaX * d, 则我们有
3. e2 = e1 + 2 * deltaY – 2 * deltaX * (y2 – y1)
4. 当e1 + 2 * deltaY > deltaX时y2 = y1 + 1, 否则y2 = y1
   终于, 没有了乘法 (2 * deltaY在循环体外计算且被简化为左移一位的运算), 没有了浮点数, 根据关系式3) 和 4), 写出算法:

// 算法4: 在算法2, 3的基础上利用递推消灭乘法和浮点数!
line_bresenham(startX, startY, endX, endY) {deltaX = endX - startX;deltaY = endY - startY;e = 0;deltaX2 = deltaX << 1;deltaY2 = deltaY << 1;drawPixel(startX, startY);for (x = startX + 1, y = startY; x <= endX; ++x) {// 关系式3) e2 = e1 + 2 * deltaY – 2 * deltaX * (y2 – y1)// 关系式4) 当e2 + 2 * deltaY > deltaX时y2 = y1 + 1, 否则y2 = y1e += deltaY2;if (e > deltaX) {e -= deltaX2;++y;}drawPixel(x, y);}
}

消灭浮点数! 代数推导

上面递推关系的推导过程是从图形上”直观”地分析得来的, 但是不严密. 我们能不能形式化地证明关系式1), 2), 3), 4)呢? 因为关系式3), 4)和1), 2)能互相推导, 我们只证明3), 4)如下:
在算法3的基础上设第n – 1次循环计算出的dist1值为e1, 对应的y值为y1, 第n次循环计算出的dist1值为e2, 对应的y值为y2. 根据算法3,
dist1 = 2 * deltaY * (x – startX) + 2 * startY * deltaX – 2 * y * deltaX, 则
e2 – e1
= 2 * deltaY * (x – startX) + 2 * startY * deltaX – 2 * y2 * deltaX – [2 * deltaY * (x – 1 – startX) + 2 * startY * deltaX – 2 * y1 * deltaX ]
= – 2 * y2 * deltaX + 2 * deltaY + 2 * y1 * deltaX
= 2 * deltaY – 2 * deltaX * (y2 – y1)
所以e2 = e1 + deltaY – deltaX * (y2 – y1). 所以我们有关系式

1. e2 = e1 + 2 * deltaY – 2 * deltaX * (y2 – y1)
2. –deltaX < e1 < deltaX
3. –deltaX < e2 < deltaX
4. y2 – y1 = 0 或者 1
   我们根据e1 + 2 * deltaY的取值范围进行讨论. 首先, 因为不等式6), 我们有
   2 * deltaY – deltaX < e1 + 2 * deltaY < 2 * deltaY + deltaX
   情况1: 如果2 * deltaY – deltaX < e1 + 2 * deltaY < deltaX, 则
   2 * deltaY – deltaX – 2 * deltaX * (y2 – y1) < e2 < deltaX– 2 * deltaX * (y2 – y1)
   反证: 若y2 – y1 = 1, 则 2 * deltaY – deltaX – 2 * deltaX < e2 < deltaX – 2 * deltaX = -deltaX, 所以y2 – y1 = 1不成立. 即情况1中y2 = y1.
   情况2: 如果 deltaX < e1 + 2 * deltaY < 2 * deltaY + deltaX, 则
   deltaX – 2 * deltaX * (y2 – y1) < e2 < 2 * deltaY + deltaX – 2 * deltaX * (y2 – y1)
   反证: 若y2 – y1 = 0, 则 deltaX < e2 < 2 * deltaY + deltaX 所以y2 – y1 = 0不成立. 即情况2中y2 = y1 + 1.
   打了这么多字, 累…以上就是当0 < k < 1的情况, 剩余几种情况 (k > 1, –1 < k < 0, k < –1. 不要挑剔我不用”>=”这种符号…) 都可以通过简单的x, y交换以及正负交换来搞定.

第一象限全方向版Bresenham算法

java版本实现如下

void lineBresenham(int startX, int startY, int endX, int endY) {int deltaX = endX - startX;int deltaY = endY - startY;int e = 0;int deltaX2 = Math.abs(deltaX << 1);int deltaY2 = Math.abs(deltaY << 1);print(startX, startY, false);boolean isSteep = deltaX>=0 ? Math.abs(deltaX)<Math.abs(deltaY) : Math.abs(deltaX)>Math.abs(deltaY);int forX0 = startX; int forY0 = startY; int forX1 = endX; int forY1 = endY;int forDeltaX2 = deltaX2; int forDeltaY2 = deltaY2;int xStep = deltaX<0 ? -1 : 1; int yStep = deltaY<0 ? -1 : 1;// 陡峭和(deltaX<0)的异或来确定是否需要做X, Y运算步骤的反转boolean isSwap = isSteep^(deltaX<0);if(isSwap) {forX0 = startY; forY0 = startX; forX1 = endY; forY1 = endX;forDeltaX2 = deltaY2; forDeltaY2 = deltaX2;xStep = deltaY<0 ? -1 : 1; yStep = deltaX<0 ? -1 : 1;}// 以长边来运算，即X必须是长边for (int x = forX0+xStep, y = forY0; (xStep>0 ? x<=forX1 : x>=forX1); x+=xStep) {e+=forDeltaY2;if(e>Math.abs(deltaX)) {e-=forDeltaX2;y=y+yStep;}print(x, y, isSwap);}
}