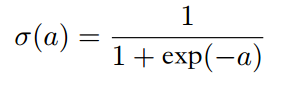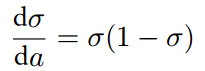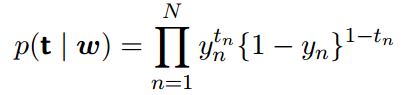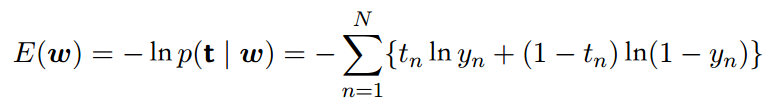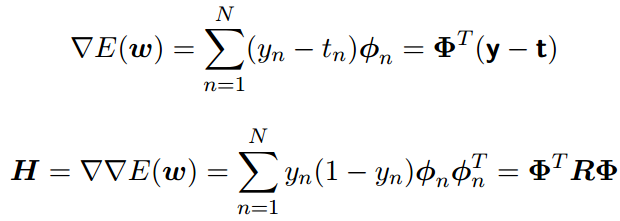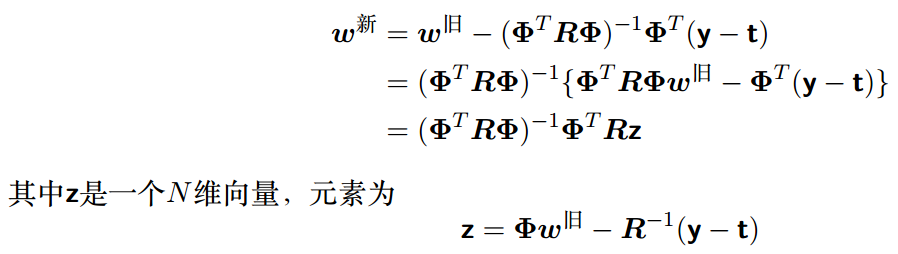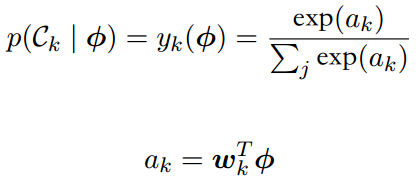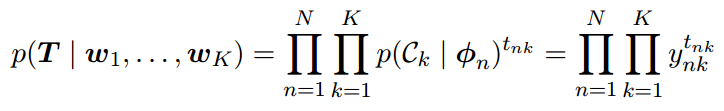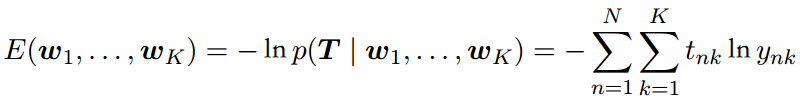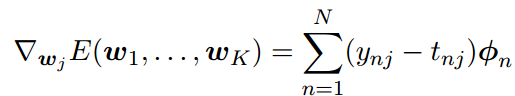分类的线性模型：概率判别式模型之逻辑回归LR

本文主要是介绍分类的线性模型：概率判别式模型之逻辑回归LR，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

http://blog.csdn.net/pipisorry/article/details/78831441

逻辑回归Logistic Regression

逻辑回归是一种线性分类模型，而不是回归模型。也就是说，输入的因变量target y是离散值，如分类类别1，0等等，而不是连续型的数据。

判别式训练的⼀种形式：在直接⽅法中，我们最⼤化由条件概率分布p(Ck j x)定义的似然函数。判别式⽅法的⼀个优点是通常有更少的可调节参数需要确定。并且预测表现也会提升，尤其是当类条件概率密度的假设没有很好地近似真实的分布的时候更是如此。

分类问题不用回归来做是因为使用回归对异常点会相当敏感。[Machine Learning - VI. Logistic Regression逻辑回归 (Week 3) ]

⾮线性变换：固定基函数

⾸先使⽤⼀个基函数向量ϕ(x)对输⼊变量进⾏⼀个固定的⾮线性变换。最终的决策边界在特征空间ϕ中是线性的，因此对应于原始x空间中的⾮线性决策边界。在特征空间ϕ(x)线性可分的类别未必在原始的观测空间x中线性可分。

对于许多实际问题来说，类条件概率密度p(x j Ck)之间有着相当⼤的重叠。这表明⾄少对于某些x的值，后验概率p(Ck j x)不等于0或1。在这种情况下，最优解可以通过下⾯的⽅式获得：对后验概率精确建模，然后使⽤第1章中讨论的标准的决策论。需要注意的是，⾮线性变换ϕ(x)不会消除这些重叠。实际上，这些变换会增加重叠的程度，或者在原始观测空间中不存在重叠的地⽅产⽣出新的重叠。然⽽，恰当地选择⾮线性变换能够让后验概率的建模过程更简单。

某小皮

逻辑回归Hypothese（二元）

⽣成式⽅法的讨论中，我们看到在⼀些相当⼀般的假设条件（指数族分布）下，类别C1的后验概率可以写成作⽤在特征向量ϕ的线性函数上的logistic sigmoid函数的形式，即

Hypothese:

σ(·)是logistic sigmoid函数：

其导数：

sigmoid 原函数及导数图形如下：

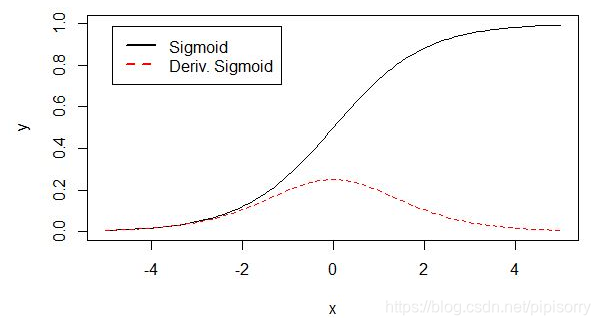
[Sigmod/Softmax变换]

对于⼀个M维特征空间ϕ，这个模型有M个可调节参数。logistic回归⽅法参数数量M是线性依赖的。

逻辑回归形式的由来：

从分类的生成式模型中可以看出，对于⼀⼤类的类条件概率密度p(x j Ck)的选择，类别C1后验概率分布可以写成作⽤于x的线性函数上的logistic sigmoid函数的形式。类似地，对于多分类的情形，类别Ck的后验概率由x的线性函数的softmax变换给出。

其它可能原因：

1 预测的是离散的类label，或者预测位于[0,1]区间的后验概率分布。所以加上非线性函数（激活函数，如sigmod）对θ的线性函数进行变换。

2 sigmoid使预测位于[0,1]，使用newton迭代求参时，Hessian矩阵正定，这样误差函数是参数的凸函数，从而具有唯一解。

3 求导方便；函数光滑什么的。广义线性？

4 根据上图，可能是可以将0-1分类更好区分，如预测4.6时就基本接近1了，loss不会有什么惩罚。感觉就像是svm只关注支持向量一般（只是LR还以小概率关注了非支持向量）。

LR的误差函数

最⼤似然MLE⽅法确定logistic回归参数

对于⼀个数据集ϕn, tn，其中tn ∈ {0;1}且ϕn = ϕ(xn)，并且n = 1, ..., N，似然函数可以写成

其中t = (t1, ...,tN)T 且yn = p(C1 | ϕn)。

另一种由来参考[对数线性模型：逻辑斯谛回归和最大熵模型]

交叉熵（ cross-entropy）误差函数

由来：通过取似然函数的负对数的⽅式，定义⼀个误差函数。这种⽅式产⽣了交叉熵（ cross-entropy）误差函数：

其中yn = σ(an)且an = wT ϕn。两侧关于w取误差函数的梯度，我们有

对数似然函数的梯度的形式⼗分简单。特别地，数据点n对梯度的贡献为⽬标值和模型预测值之间的“误差”yn − tn与基函数向量ϕn相乘。函数形式与线性回归模型中的平⽅和误差函数的梯度的函数形式完全相同。

MLE方法解LR的缺陷

正则化和欠约束：机器学习中许多线性模型，包括线性回归和 PCA，都依赖于求逆矩阵 s⊤s。只要 s⊤s 是奇异的这就是不可能的。每当数据生成分布的一些方向上确实没有差异时，或因为例子较少（即相对输入特征（ s 的列）来说）而在一些方向没有观察到方差，这个矩阵就是奇异的。在这种情况下，正则化的许多形式对应于求逆 s⊤s + αA。这个正则化矩阵可以保证是可逆的。

相关矩阵可逆时，这些线性问题有闭式解。没有闭式解的问题也可能是欠定的。一个例子是应用于线性可分问题的逻辑回归。如果权重向量 r 能够实现完美分类，那么 2r 也会以较高似然实现完美分类。类似随机梯度下降的迭代优化算法将持续增加 r 的大小，理论上永远不会停止。在实践中，数值实现的梯度下降最终会达到导致数值溢出的超大权重，此时的行为将取决于程序员如何处理这些不是真正数字的值。

[深度学习]

最⼤似然⽅法对于线性可分的数据集会产⽣严重的过拟合现象。这是由于最⼤似然解出现在超平⾯对应于σ = 0.5的情况，它等价于wT ϕ = 0。最⼤似然解把数据集分成了两类，并且w的⼤⼩趋向于⽆穷⼤（lz: 为了使最大似然更大）。这种情况下， logistic sigmoid函数在特征空间中变得⾮常陡峭，对应于⼀个跳变的阶梯函数，使得每⼀个来⾃类别k的训练数据都被赋予⼀个后验概率p(Ck j x) = 1。此外，通常这些解之间存在连续性，因为任何切分超平⾯都会造成训练数据点中同样的后验概率，正如图10.13。最⼤似然⽅法⽆法区分某个解优于另⼀个解，并且在实际应⽤中哪个解被找到将会依赖于优化算法的选择和参数的初始化。

注意，即使与模型的参数相⽐数据点的数量很多，只要数据是线性可分的，这个问题就会出现。通过引⼊先验概率，然后寻找w的MAP解，或者等价地，通过给误差函数增加⼀个正则化项，这种奇异性就可以被避免。

[PRML]

LR的参数学习

误差函数是凸函数，因此有⼀个唯⼀的最⼩值。

梯度下降法

参考[Machine Learning - VI. Logistic Regression逻辑回归 (Week 3) ]

迭代重加权最⼩平⽅（IRLS，iterative reweighted least squares）

Newton-Raphson迭代最优化框架，使⽤了对数似然函数的局部⼆次近似。lz：应该就是牛顿迭代法在LR学习上的应用吧。

权值的更新的形式

H是⼀个Hessian矩阵，它的元素由E(w)关于w的⼆阶导数组成。

把Newton-Raphson更新应⽤到logistic回归模型的交叉熵误差函数上。误差函数的梯度和Hessian矩阵为

我们引⼊了⼀个N × N的对⾓矩阵R，元素为Rnn = yn(1 − yn) 。我们看到Hessian矩阵不再是常量，⽽是通过权矩阵R依赖于w。这对应于误差函数不是⼆次函数的事实。使⽤性质0 < yn < 1（这个性质来⾃于logistic sigmoid函数形式），我们看到对于任意向量u都有uT Hu > 0，因此Hessian矩阵H是正定的。因此误差函数是w的⼀个凸函数，从⽽有唯⼀的最⼩值。

这样， logistic回归模型的Newton-Raphson更新公式就变成了

由于权矩阵R不是常量，⽽是依赖于参数向量w，因此我们必须迭代地应⽤规范⽅程，每次使⽤新的权向量w计算⼀个修正的权矩阵R（与加权的最⼩平⽅问题⼀样，对⾓矩阵R可以看成⽅差）。由于这个原因，这个算法被称为迭代重加权最⼩平⽅（ iterative reweighted least squares），或者简称为IRLS（ Rubin, 1983）。

某小皮