动态规划简述；斐波那契数列自顶向下和自底向上

本文主要是介绍动态规划简述；斐波那契数列自顶向下和自底向上，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

概述

动态规划就是把一个问题分解为若干子问题，把子问题的解累加起来，就是当前问题的值。

斐波那契数列（自顶向下）

一个很好的演示demo，
在进行运算时，要用上备忘录（缓存），不然会有重复计算，速度会很慢

public static void main(String[] args) {long n = 1000;Map<Long,Long> cache = new HashMap<>();StopWatch stopWatch = new StopWatch();stopWatch.start();System.out.println(calc(n, cache));stopWatch.stop();System.out.println(stopWatch.getTime() + "毫秒");
}public static long calc(Long n, Map<Long,Long> cache){if(n == 0 || n == 1) return 1;if(null != cache.get(n)) return cache.get(n);long result = calc(n - 1, cache) + calc(n - 2, cache);cache.put(n, result);return result;
}

捞一张大佬的斐波那契数列分解图

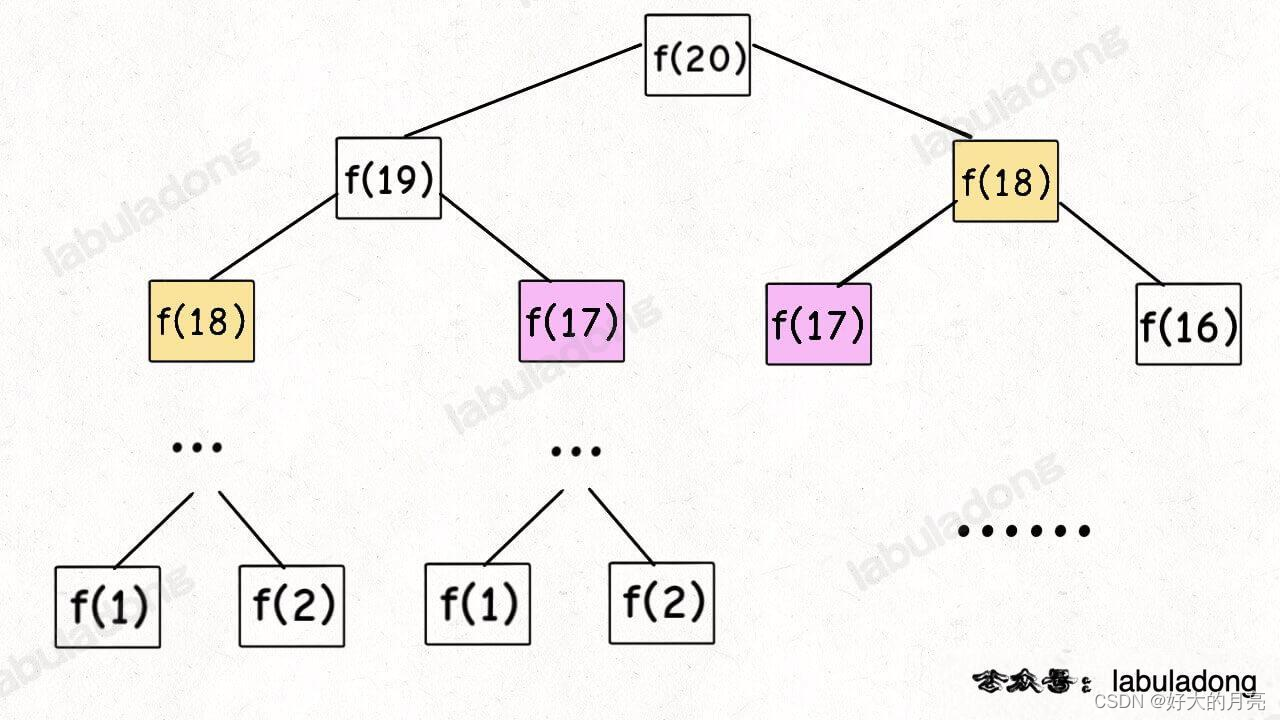
斐波那契数列（自底向上）

意思就是从基础开始计算，直到计算得到目标值

 public static void main(String[] args) {StopWatch stopWatch = new StopWatch();stopWatch.start();System.out.println(calcFloor2Up(5000));stopWatch.stop();System.out.println(stopWatch.getTime() + "毫秒");
}public static Long calcFloor2Up(int n){long[] dp = new long[n+1];dp[0] = 0;dp[1] = 1;for (int i = 2; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];
}public static void main(String[] args) {StopWatch stopWatch = new StopWatch();stopWatch.start();System.out.println(calcFloor2UpV2(1000));stopWatch.stop();System.out.println(stopWatch.getTime() + "毫秒");
}//更快的版本，空间复杂度O(1)
public static int calcFloor2UpV2(int n){if (n == 0 || n == 1) {// base casereturn n;}// 分别代表 dp[i - 1] 和 dp[i - 2]int dp_i_1 = 1, dp_i_2 = 0;for (int i = 2; i <= n; i++) {// dp[i] = dp[i - 1] + dp[i - 2];int dp_i = dp_i_1 + dp_i_2;// 滚动更新dp_i_2 = dp_i_1;dp_i_1 = dp_i;}return dp_i_1;
}

这篇关于动态规划简述；斐波那契数列自顶向下和自底向上的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---