底向上专题
专题---自底向上的计算机网络(计算机网络相关概述)
目录 计算机网络相关概述 物理层 数据链路层 网络层 运输层 应用层 网络安全 1.计算机网络相关概述(具体细节http://t.csdnimg.cn/NITAW) 什么是计算机网络? 计算机网络是将一个分散的,具有独立功能的计算机系统,通过通信设备与线路连接起来,由功能完善的软件实现资源共享和信息传递的系统。 计算机网络有什么组成? 从不同角度出发看待计算机网络的组成,结
动态规划之钢条切割问题自底向上发的实现(算法导论第15章)
看算法导论的同学应该知道第15章在讲动态规划,以钢条切割问题作为引论,那么钢条切割问题实际的C代码是怎么实现的呢?图表和题目我就不叙述了,直接看代码 // steercut.cpp : Defines the entry point for the console application.//// 钢条切割问题.cpp : Defines the entry point for the c
ABAQUS软件实训(六):Mesh模块之自底向上的网格划分
所谓自底向上网格划分,就是从二维的网格划分,拉伸或扫掠成三维的网格。 一、绘制实体 先新建一个实体: 得到实体: 二、自底向上的网格划分 设置网格划分为Bottom-up,如图所示: (我悄悄把旋转角度改成了180度,纯粹看着舒服点) Sweep Method 如果把几何体当做扫掠,选择Sweep: 选择完成后,点击mesh即可: 还可以对网格划分密度
python自底向上的执行单元测试
在上一篇博客(python自顶向下的设计方法进行体育竞技分析,网址:http://blog.csdn.net/sxingming/article/details/51235650)中, 我们学习了自顶向下的设计:从顶层开始分解问题为更小的问题进行求解。程序写好后,需要通过运行程序进行测试, 测试的好方法也是分成小部分进行展开,即自底向上的执行:从底层模块开始一个一个进行测试,直至整个系统测试完
LeetCode 2673.使二叉树所有路径值相等的最小代价:自顶向下的DFS 或 自底向上的递推
【LetMeFly】2673.使二叉树所有路径值相等的最小代价:自顶向下的DFS 或 自底向上的递推 力扣题目链接:https://leetcode.cn/problems/make-costs-of-paths-equal-in-a-binary-tree/ 给你一个整数 n 表示一棵 满二叉树 里面节点的数目,节点编号从 1 到 n 。根节点编号为 1 ,树中每个非叶子节点 i 都有两个孩
《自底向上从零实现数字化工厂》作者:吴占校
始于2024-02-07 22:10(“伴山听雨”-“归来”) 由于业余时间创作,当前您看到的仅为草稿,可能会随时修改,敬请谅解。 本书适合从事数字化工厂软件开发人员、分析和设计人员,适合制造型企业数字化转型的决策人员,适合将新建数字化工厂的企业。 第一章 数字化工厂概述 摘要 本书旨在实现工厂数字化,将从技术层面到业务层甚至到企业战略层面,对制造业数字化进行代码层面的实现,将以Java代
二叉树自顶向下递归和自底向上递归
二叉树自顶向下递归 自顶向下(top-down) 和前序遍历紧密关联(根->左->右)当前节点的情况依赖于其父节点的情况考虑完父节点,再考虑当前节点 LeetCode 104. 二叉树的最大深度 class Solution {int ans;public int maxDepth(TreeNode root) {ans = 0;dfs(root, 0);return ans;}// 自顶
U4_3 语法分析-自底向上分析-LR0/LR1/SLR分析
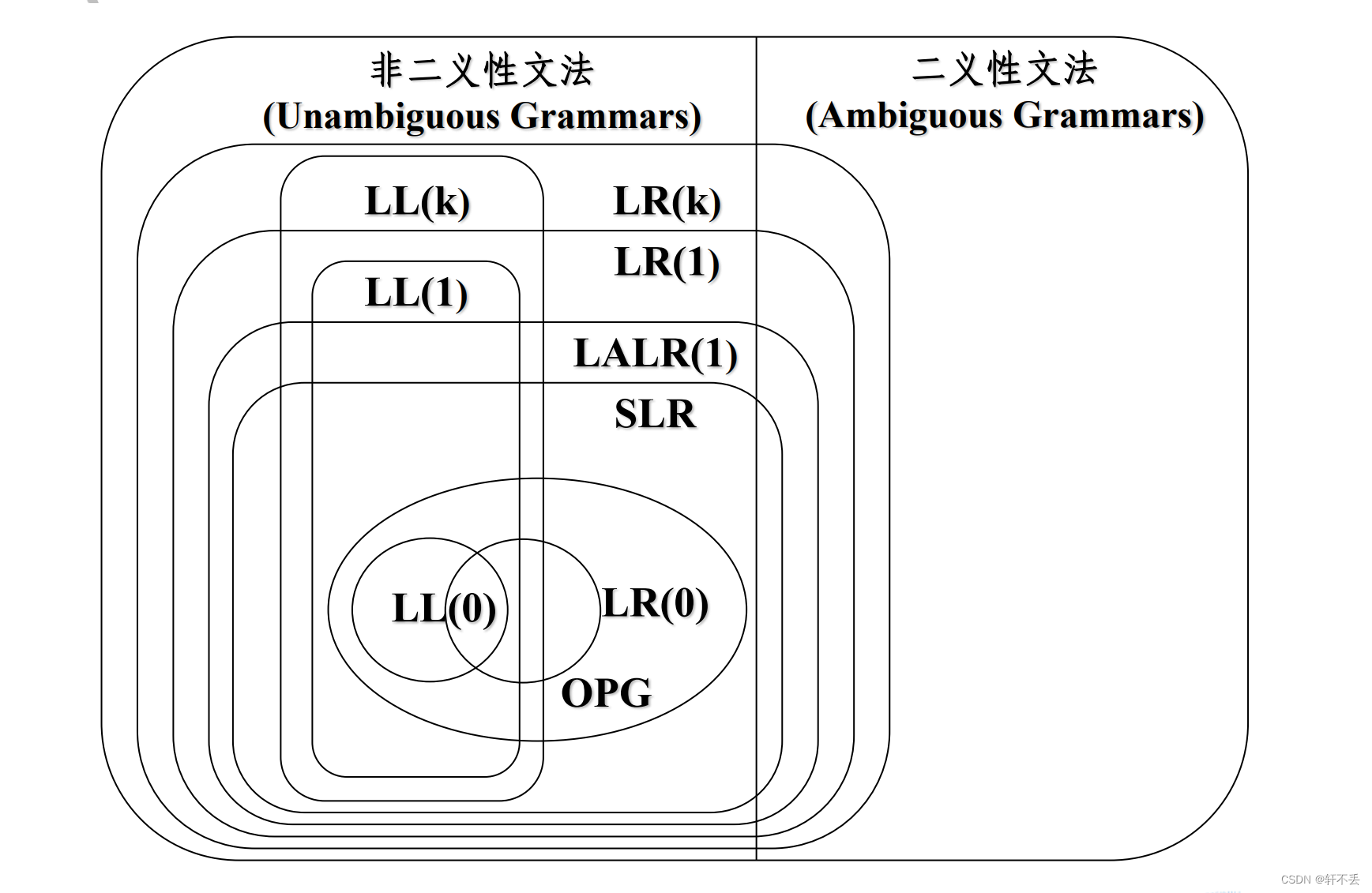
文章目录 一、LR分析法1、概念2、流程3、LR分析器结构及分析表构造1)结构2)一些概念 二、LR(0)分析法1、流程2、分析动作1)移近2)归约(reduce) 3、总结1)LR分析器2)构造DFA3)构造LR(0)的方法(三步) 4、局限性 三、LR(1)分析法四、SLR(1):简单LR分析法1、基本思想2、分析思路1)构建表2)SLR求ACTION表 3、局限性 五、彩蛋
编译原理----算符优先级的分析(自底向上)
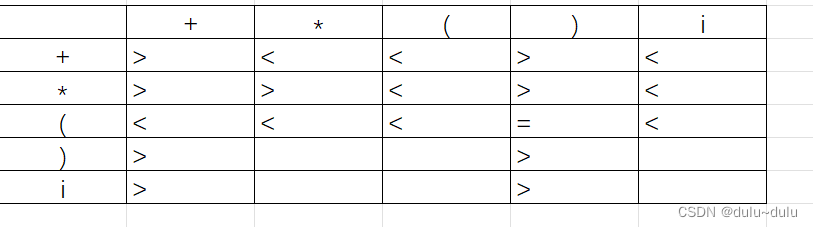
自底向上分析的分类如下所示: 算符优先分析 算符优先分析只规定算符之间的优先关系,也就是只考虑终结符之间的优先关系。 (一)若有文法G,如果G没有形如A->..BC..的产生式,其中B和C为非终结符,则称G为算符文法。 以下例子中G就是算符文法(没有连在一起的非终结符) E->T|E+T|E-T T->F|T*F|T/F F->(E)|i (二) 这里就用=,< 和 >
9月5日关键点检测学习笔记——人体骨骼点检测:自底向上
文章目录 前言一、堆叠沙漏网络 Stacked Hourglass Networks1、Hourglass Module2、Heat map 二、自顶向下的问题三、自底向上1、OpenPose 四、OpenPose 实战 前言 本文为9月5日关键点检测学习笔记——人体骨骼点检测:自底向上,分为四个章节: 堆叠沙漏网络 Stacked Hourglass Networks;自
动态规划简述;斐波那契数列自顶向下和自底向上
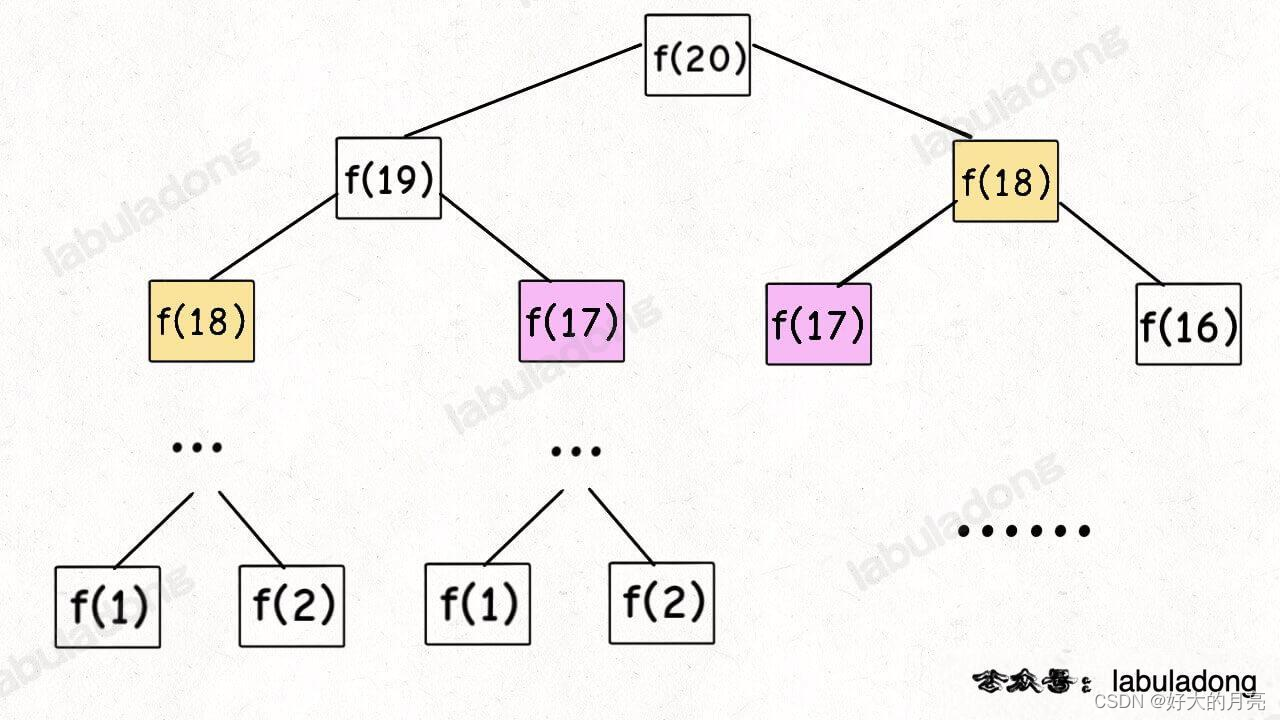
概述 动态规划就是把一个问题分解为若干子问题,把子问题的解累加起来,就是当前问题的值。 斐波那契数列(自顶向下) 一个很好的演示demo, 在进行运算时,要用上备忘录(缓存),不然会有重复计算,速度会很慢 public static void main(String[] args) {long n = 1000;Map<Long,Long> cache = new HashMap<>();