2D凸包算法（一）：Jarvis' March （ Gift Wrapping Algorithm ）

Jarvis’ March 图示

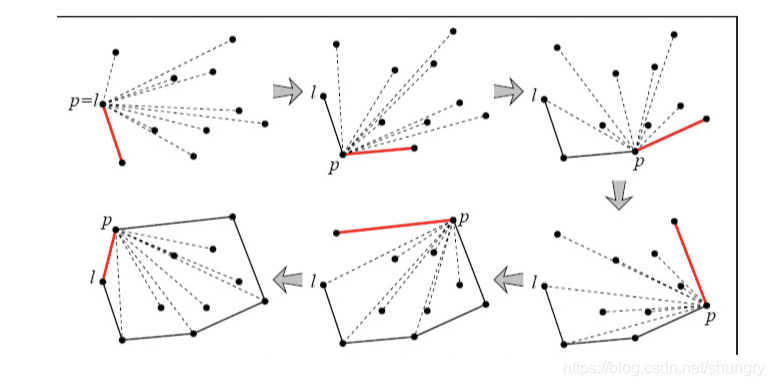
先从一个凸包上的顶点开始，顺着外围绕一圈。
每当寻找下一个要被包围的点，则遍历平面上所有点，找出最外围的一点来包围。可以利用叉积运算来判断。

• 时间复杂度为 O(NM) ， N 为所有点的数目， M 为凸包的顶点数目。

具体思想：

1. 先确定边界上的点v1和与下一个点v2
2. 在点集里去寻找下一个点v3，使得v1 v3 v2满足CCW
3. 如果满足，这就说明v3是更外围的点
4. 把v3的值覆盖v2，即v2 = v3
5. 重复的3步，直到所有点都访问过，即为找到了下一个最外边的点
6. 将v2的值覆盖v1，即v1 = v2
7. 重复第2步，直到下一个点回到起点

CCW：counterclockwise 以逆时针方向旋转

Jarvis’ March 代码

typedef vector<pair<double, double>> vpdd;
typedef pair<double, double> pdd;bool ccw(pdd a, pdd b, pdd c)
{return ((c.first - a.first) * (b.second - a.second) - (c.second - a.second) * (b.first - a.first)) < 0;
}
void jarvis_march(const vpdd &input)
{int n = input.size();int left = 0;for (int i = 0; i < n; i++){if (input[i].first < input[left].first){left = i;}}int first_point = left;int third_point;do{hull_jmarch.push_back(input[first_point]);// cout<<"here\n";third_point = (first_point + 1) % n;for (int i = 0; i < n; i++){if (ccw(input[first_point], input[i], input[third_point])){third_point = i;}}first_point = third_point;} while (first_point != left);
}