wrapping专题
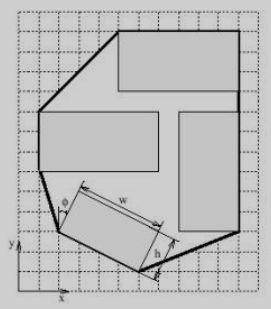
【UVA】10652-Board Wrapping(凸包问题)
又增加了2个模板。 #include <iostream>#include <cstdlib>#include <cstdio>#include <string>#include <cstring>#include <cmath>#include <vector>#include <queue>#include <stack>#include <algorithm>usi
8. Wrapping Chocolate
题目链接:Wrapping Chocolate n n n 盒巧克力和 m m m 个盒子有各自的长和宽,巧克力只能放进长宽均不小于自己的盒子,不能转过来放,问能不能把所有巧克力都放进去。 只要想办法把一个维度消掉,就很容易解决这个问题。 可以把盒子和巧克力放一起,对宽度从大到小排序,盒子永远放在最前面。这样枚举的时候宽度的要求就直接满足了,然后维护一下可用的盒子的长度即可。 #inc
uva 10652 Board Wrapping
原题: The small sawmill in Mission, British Columbia, has developed a brand new way of packaging boards for drying. By fixating the boards in special moulds, the board can dry efficiently in a drying r
凸包(Convex Hull)问题求解--Gift-Wrapping 算法
凸包问题(Convex Hull)求解--卷包裹(Gift-Wrapping) 算法 1.前言 最近在做MIT 6.031的问题集0时遇到了要计算凸包的问题,题中提示要用Gift Wrapping算法。作为一个在实际工程中需要应用的求解算法来讲它并不是最好的,因为它有着的时间复杂度,但是我们依然可以通过它更好地理解问题的实质。更好地学习和应用这个基本算法。 2.Conv
abc E - Wrapping Chocolate
题目传送门:E - Wrapping Chocolate 题目大意: 有n块给出长和宽的巧克力和m个给出长和宽的盒子,要求能把巧克力都装进盒子里。 思路:长和宽二维合起来考虑的话将会非常困难,所以应将盒子和巧克力的数组合起来对一个元素作为主键排序,然后从最大开始,每次遇到盒子的数组就把非主键元素放入集合,遇到巧克力数组就以其非主键元素在集合内查找,找到最小的且不小于当前元素的值并删除,找不到就代表
cgal教程 3D Alpha Wrapping
文章目录 3D Alpha Wrapping (3D alpha 包裹)1 介绍2 方法2.1 算法2.2 保证 3 接口4 选择参数4.1 alpha4.2 Offset4.3 关于“双面”包裹的注意事项 5 性能6 例子 3D Alpha Wrapping (3D alpha 包裹) 原文地址: https://doc.cgal.org/latest/Alpha_wrap_
2D凸包算法(一):Jarvis' March ( Gift Wrapping Algorithm )
Jarvis’ March 图示 先从一个凸包上的顶点开始,顺着外围绕一圈。 每当寻找下一个要被包围的点,则遍历平面上所有点,找出最外围的一点来包围。可以利用叉积运算来判断。 时间复杂度为 O(NM) , N 为所有点的数目, M 为凸包的顶点数目。 具体思想: 先确定边界上的点v1和与下一个点v2在点集里去寻找下一个点v3,使得v1 v3 v2满足CCW如果满足,这就说明v
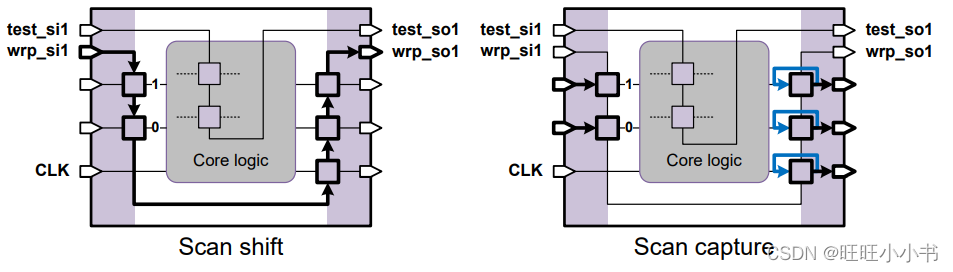
可测试性设计原理:Wrapping Core (Ⅱ)
Wrapping core 本文主要讲述了The Simple Core Wrapping Flow的基本原理,区别于The Maximized Reuse Core Wrapping Flow实现更为简单,但会引入更大的timing和area的影响。参考(翻译)自《Synopsys® TestMAX™ DFT User Guide》,FYI。 The Simple Core Wra