uva 10652 Board Wrapping

本文主要是介绍uva 10652 Board Wrapping，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

原题：
The small sawmill in Mission, British Columbia, has developed a brand new way of packaging boards for drying. By fixating the boards in special moulds, the board can dry efficiently in a drying room.Space is an issue though. The boards cannot be too close, because then the drying will be too slow.On the other hand, one wants to use the drying room efficiently.Looking at it from a 2-D perspective, your task is to calculate the fraction between the space occupied by the boards to the total space occupied by the mould. Now, the mould is surrounded by an aluminium frame of negligible thickness, following the hull of the boards’corners tightly. The space occupied by the mould would thus be the interior of the frame.

Input
On the first line of input there is one integer, N ≤ 50,giving the number of test cases (moulds) in the input. After this line, N test cases follow. Each test case starts with a line containing one integer n, 1 < n ≤ 600, which is the number of boards in the mould.
Then n lines follow, each with five floating point numbers x, y, w, h, ϕ where 0 ≤ x,y,w,h ≤ 10000
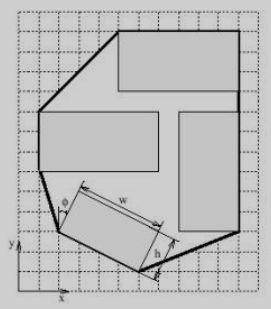
and −90 ◦ < ϕ ≤ 90 ◦ . The x and y are the coordinates of the center of the board and w and h are the width and height of the board, respectively. ϕ is the angle between the height axis of the board to the y-axis in degrees, positive clockwise. That is, if ϕ = 0, the projection of the board on the x-axis would be w. Of course, the boards cannot intersect.
Output
For every test case, output one line containing the fraction of the space occupied by the boards to the total space in percent. Your output should have one decimal digit and be followed by a space and a percent sign (‘%’).
Note: The Sample Input and Sample Output corresponds to the given picture
Sample Input
1
4
4 7.5 6 3 0
8 11.5 6 3 0
9.5 6 6 3 90
4.5 3 4.4721 2.2361 26.565
Sample Output
64.3 %

中文：
给你一堆矩形，然后告诉你矩形的长宽，以及矩形的中心坐标，以及矩形绕着自身中心的旋转度数。让你把这些矩形用直线圈起来。最后问你这些矩形占你圈出来的面积的百分比。

#include <bits/stdc++.h>
#define Vector Point
using namespace std;
//fstream in,out;
const int maxn=2405;
const double PI=acos(-1);
double torad(double deg)
{return deg/180*PI;
}
struct Point
{double x,y;Point(double x=0,double y=0):x(x),y(y){}
};bool operator < (const Point &a,const Point &b)
{return a.x<b.x||(a.x==b.x&&a.y<b.y);
}
Vector operator +(Vector A,Vector B){return Vector(A.x+B.x,A.y+B.y);}
Vector operator -(Vector A,Vector B){return Vector(A.x-B.x,A.y-B.y);}
double Cross(Vector A,Vector B)
{return A.x*B.y-A.y*B.x;
}
int ConvexHull(Point *p,int n,Point *ch)
{sort(p,p+n);int m=0;for(int i=0;i<n;i++){while(m>1&&Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0)m--;ch[m++]=p[i];}int k=m;for(int i=n-2;i>=0;i--){while(m>k&&Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0)m--;ch[m++]=p[i];}if(n>1)m--;return m;
}
Vector Rotate(Vector A,double rad)//旋转
{return Vector(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));
}
double PolyonArea(Point* p,int n)//多边形面积
{double area=0;for(int i=1;i<n-1;i++)area+=Cross(p[i]-p[0],p[i+1]-p[0]);return area/2;
}
int main()
{ios::sync_with_stdio(false);int t,n;Point P[maxn],ch[maxn];cin>>t;while(t--){int pc=0;double x,y,w,h,j,ang,board,hull;board=hull=0;cin>>n;for(int i=0;i<n;i++){cin>>x>>y>>w>>h>>j;Point o(x,y);ang=-torad(j);P[pc++]=o+Rotate(Vector(-w/2,-h/2),ang);P[pc++]=o+Rotate(Vector(w/2,-h/2),ang);P[pc++]=o+Rotate(Vector(-w/2,h/2),ang);P[pc++]=o+Rotate(Vector(w/2,h/2),ang);board+=w*h;}int m=ConvexHull(P,pc,ch);hull=PolyonArea(ch,m);cout<<fixed<<setprecision(1)<<board*100/hull<<" %"<<endl;}return 0;
}

解答：
我的第一道凸包题目，这题就是裸题，代码来自刘汝佳的白书。很好的模板，凸包算法为andrew算法，非常好理解，自己在纸上画一画就能明白。

这篇关于uva 10652 Board Wrapping的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---