开源代码分享(6)—考虑实时市场联动的电力零售商鲁棒定价策略(附matlab代码)

本文主要是介绍开源代码分享(6)—考虑实时市场联动的电力零售商鲁棒定价策略(附matlab代码)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

摘要：电力零售商作为连接电力批发市场与零售市场的桥梁，是电力市场化改革中的重要主体，其经营效率直接决定了市场化改革的成败。然而电力零售商在运营过程中面临着用电量需求和价格双重不确定性的市场风险，亟需通过优化市场行为以保障自身的利益。为此提出了考虑实时市场联动

的电力零售商鲁棒定价策略，以提升其抗风险能力。首先，考虑电力零售商日前定价、日前购电、实时能量管理、电动车用户需求响应和电力市场统一出清价格等因素，建立了考虑电动汽车不确定性的电力零售商鲁棒定价模型。然后，通过线性化方法将鲁棒定价模型转化为两阶段混合整数规

划，并通过列与约束生成算法迭代求解。最后，在 IEEE-33节点测试系统上进行了仿真，结果表明所提策略充分考虑了市场不确定性因素的影响，利用对冲机制降低了市场风险，提高了电力零售商的经营效率。

关键词：电力现货市场；需求响应；零售定价；鲁棒优化

DOI ： 10.13335/j.1000-3673.pst.2021.2157

1 电力零售商鲁棒定价模型陈述

以电动汽车运营商为例，电力零售商典型的运营模式如图 1 所示。

在图 1 中，由于电力零售商自身不具备发电资源，因此其需要通过日前电力市场与实时电力市场向上级电网购买电能。另一方面，电力零售商向电动汽车等电力用户发布零售电价，并保证用户电能计划的顺利完成。同时，在实际运行中电力零售商能通过能量管理系统控制储能系统的充放电量，从而具备向实时电力市场售电的能力。在此过程中，零售商与上级电网的电能交换将按照其所在配电网电气位置的 DLMP 结算，而零售商与电力用户的电能交换则按照零售电价结算。零售商需要考虑的问题是：零售电价必须在日前发布，而电力用户的属性无法未卜先知，难以针对性的设计零售电价。为此，论文假设零售用户为电动汽车用户，考虑实际参与零售市场的电动汽车集合不确定性，建立了如图 2 所示的电力零售商鲁棒定价模型，旨在帮助电力零售商规避风险。

如图 2 所示，鲁棒定价模型的目标是使得零售商收益最大化，决策变量包括日前购电量和零售电价，并需要满足日前市场交易规则约束、零售市场定价约束和电能平衡约束。在此过程中，日前市场出清模型作为边界条件，描述了日前购电决策与出清价格的映射关系；用户需求响应模型同样作为边界条件，描述了零售电价与电能计划的映射关系。实时决策作为模型中的子问题，通过优化储能和实时购售电量实现了实时阶段的电能调整，其中实时市场的电价曲线由先验知识确定，作为模型中的外生变量。最后，论文考虑了零售用户集合的不确定性，建立了鲁棒优化模型，从而计算最不利条件下的零售商决策与收益。

1.1 电力零售商日前决策模型

在日前(day-ahead，DA)阶段，电力零售商需要决策其在日前电力市场中的购电量并发布其零售价格，以期实现自身的收益最大化，因此其目标函数由式 (1) 描述，其包含日前购电成本与实时

(real-time ， RT) 运行期望收益两部分。

1.2 电力零售商实时决策模型

在实时阶段，电力零售商的能量管理系统将根据实际电动汽车 (electric vehicle ，EV)充放电量优化电能计划，包括储能系统(energy storage system，ESS)的充放电量以及对实时电力市场的购售电量。另一方面，由于实时电价无法未卜先知，因此电力零售市场将考虑实时电价的随机性，建立期望效用模型。电力零售商的实时期望收益如式(5)所示，其包含电动汽车的支付费用、实时购电成本和实时售电收入。

1.3 电动汽车不确定集的描述

由上述模型可知电力零售商日前发布的零售价格决定了电动汽车用户的需求响应行为，然而实际电动汽车的行为偏好无法未卜先知，因此电力零售商日前定价决策中需要考虑的不确定变量为电动汽车集合 $N^{EV}$ ，以确保在电动汽车信息不确定的情况下仍能够签订合适的日前购电合同以及制定最优的零售电价。

不同于风电出力等不确定变量，电动汽车集合包含有多种属性，且不同属性间有着强烈的相

关性。同时电动汽车的数量庞大，因此电动汽车集合的不确定空间难以刻画。为此本文借助多离

散场景分布鲁棒优化的思想，根据历史数据将电动汽车聚类为 $N_{type}$ 类，从而考虑每类电动汽车概率的不确定性，从而由式(13)描述电动汽车集群的充放电量。

由于聚类所使用的样本数量有限，其得到的经验分布与实际分布存在误差，因此本文通过式(14)描述有限类型电动汽车占比构成的不确定空间 [25] 。

至此，式(1)对应的鲁棒定价模型转化为式(15)所示模型，其物理意义为：电力零售商根据经验将电动汽车分为 $N_{type}$ 种类型，并考虑每类电动汽车数量的不确定性，决策其日前购电量和零售价格，使得在电动汽车最坏组合的情况下零售商能实现最大收益。

2 基于列与约束生成算法的两阶段鲁棒优化求解策略

上述模型构成了两阶段鲁棒优化问题[27]，本节将基于 CCG 算法求解上述模型。

2.1 模型的紧凑形式

首先根据文献[14] 和 [28] 中的方法消除式 (8)和式 (11) 的非线性，进一步利用场景法处理实时

DLMP 的不确定性，将期望算子退化为有限场景的求和算子，从而得到电力零售商鲁棒定价的紧凑形式，如式 (16) 所示。

2.2 模型求解过程

上述模型构成了多阶段多层规划，无法直接求解。因此本文将其分解为鲁棒优化主问题和子问题，并利用 CCG 算法迭代求解。

鲁棒优化主问题定义见附录 C，其物理意义为：在给定的电动汽车组合下，电力零售商优化日前购电量和零售电价，从而实现自身的收益最大化。鲁棒优化子问题的定义见附录 D，其物理意义为：在已知日前购电合同和零售价格的条件下，考虑能量管理系统的实时优化调度，找到最坏的电动汽车组合。

由此，电力零售商优化其日前购电量和零售价格的步骤如下所示。

文献[29] 证明了 CCG 算法具有良好的收敛性，能够在有限次迭代后得到最优解。

需要注意的是，上述流程中默认了鲁棒优化子问题均存在可行解。当鲁棒优化子问题不可行时，需要引入松弛变量重新求解子问题，并向主问题返回不可行割[30]。然而本文所研究的场景假设零售商所在电气节点的配变有足够的容量，不存在实时电能需求无法满足的情况，因此忽略了鲁棒优化子问题不可行的情况。

3 数值仿真分析

本文在 IEEE 33 节点配电系统[31]中进行了数值仿真分析，以验证所提鲁棒定价策略的有效性。。仿真是在 64 位 Windows 10操作系统中通过 MATLAB R2014a 编程并调用YALMIP 和 GUROBI 9.0[32]完成的，仿真时段为24h。仿真系统的参数如下。

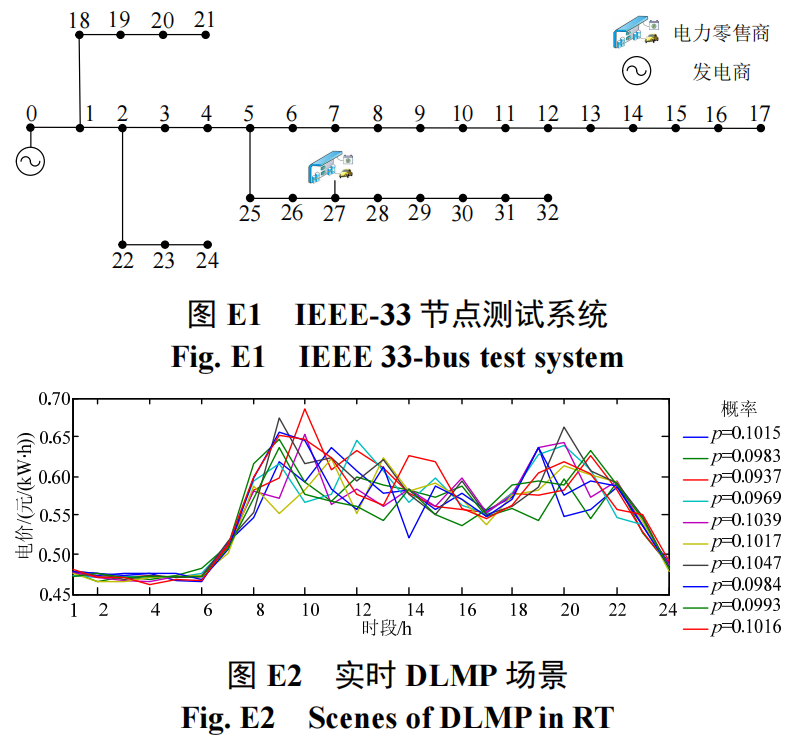
IEEE 33节点配电系统共有32个配电变压器，32条支路，其电压等级为12.66kV，功率基准值为100MVA，最大基础负荷为3715+j2300kVA，节点0为平衡节点，其电压为1.05 p.u.，其拓扑结构如图1所示，线路与配变参数如表1所示。

表1 IEEE 33节点配电系统参数

节点i	节点 j	阻抗 (Ω)	负荷 (kVA)	节点i	节点j	阻抗 (Ω)	负荷 (kVA)
0	1	0.0922+j0.047	100+j60	16	17	0.3720+j0.5740	90+j40
1	2	0.4930+j0.2511	90+j40	1	18	0.1640+j0.1565	90+j40
2	3	0.3660+j0.1864	120+j80	18	19	1.5042+j1.3554	90+j40
3	4	0.3811+j0.1941	60+j30	19	20	0.4095+j0.4784	90+j40
4	5	0.8190+j0.7070	60+j20	20	21	0.7089+j0.9373	90+j40
5	6	0.1872+j0.6188	200+j100	2	22	0.4512+j0.3083	90+j50
6	7	0.7114+j0.2351	200+j100	22	23	0.8980+j0.7091	420+j200
7	8	1.0300+j0.7400	60+j20	23	24	0.8960+j0.7011	420+j200
8	9	1.0440+j0.7400	60+j20	5	25	0.2030+j0.1034	60+j25
9	10	0.1966+j0.0650	45+j30	25	26	0.2842+j0.1447	60+j25
10	11	0.3744+j0.1238	60+j35	26	27	1.0590+j0.9337	60+j20
11	12	1.4680+j1.1550	60+j35	27	28	0.8042+j0.7006	120+j70
12	13	0.5416+j0.7129	120+j80	28	29	0.5075+j0.2585	200+j600
13	14	0.5910+j0.5260	60+j10	29	30	0.9744+j0.9630	150+j70
14	15	0.7463+j0.5450	60+j20	30	31	0.3105+j0.3619	210+j100
15	16	1.2890+j1.7210	60+j20	31	32	0.3410+j0.5362	60+j40

配电网的基础负荷曲线如图2所示，其中时段1代表00:00-01:00。

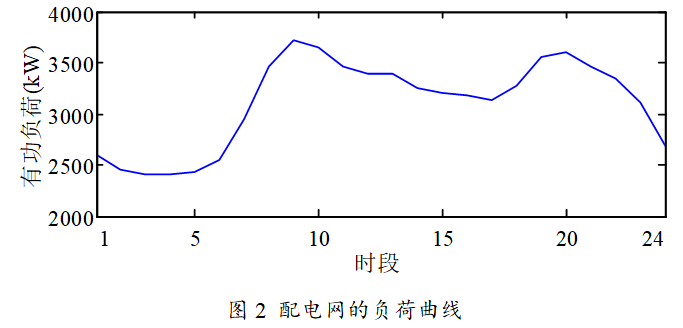
表2 日前电力批发市场基础电价

时段	1	2	3	4	5	6	7	8
电价(元/kWh)	0.4148	0.3931	0.3875	0.3856	0.3900	0.4062	0.4664	0.5442
时段	9	10	11	12	13	14	15	16
电价(元/kWh)	0.5836	0.5718	0.5432	0.5324	0.5321	0.5122	0.5066	0.5028
时段	17	18	19	20	21	22	23	24
电价(元/kWh)	0.4933	0.5168	0.5572	0.5651	0.5442	0.5258	0.4911	0.4278

电力零售商拥有一个容量为 1000kW . h 的储能系统，其最大充放电功率均为 250kW，储能系统的充放电效率均为 0.95，储能系统荷电状态的安全范围为 20% 至 95% ，在 08:00 时储能系统的电量为500kW . h。同时电力零售商代理充电站参与市场交易，其零售电价的下限为 DLMP 的 0.8 倍，零售电价的上限为 DLMP 的 1.2 倍，零售电价的平均值等于全天 DLMP 的平均值。电力零售商通过电气节点27 接入配电网，其最大日前购电量为 500kW . h，最大实时购售电量均为 500kW . h 。

论文将 1000 个历史电动汽车数据聚类成 10 类，并假设充电站平均每天服务的电动汽车数量为 50，电动汽车的充放电效率均为 0.95，电动汽车电池荷电状态的安全范围为 20% 至 95%，假设电动汽车的期望电量均为 95%的电池容量，电动汽车的单位效用均为 1 元 /(kW . h) 。置信度 α 1 和 α ∞ 均为 0.99 。