矩陣的運算

2023-10-12 01:08

文章标签 矩陣運算

本文主要是介绍矩陣的運算，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

http://blog.csdn.net/as3_flash/article/details/2378453

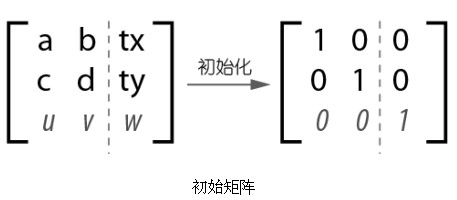
把一組數字記錄成矩陣形式是沒有意義的，學習矩陣的關鍵在於掌握矩陣之間的運算。

1．矩陣加法運算

矩陣之間也可以相加。把兩個矩陣對應位置的單個元素相加，得到的新矩陣就是矩陣加法的結果。由其運算法則可知，只有行數和列數完全相同的矩陣才能進行加法運算。

矩陣之間相加沒有順序，假設A、B都是矩陣，則A+B=B+A。通常認為矩陣沒有減法，若要與一個矩陣相減，在概念上是引入一個該矩陣的負矩陣，然後相加。A-B是A+(-B)的簡寫。圖演示了兩個三行三列矩陣的加法。

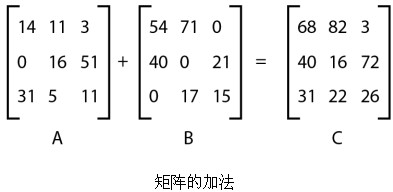
矩陣加法在圖像位移運算時經常用到。

2．矩陣乘法運算

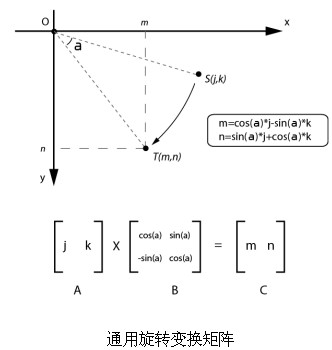
矩陣之間也可以進行乘法運算，但其運算過程相對複雜得多。與算術乘法不同，矩陣乘法並不是多個矩陣之和，它有自己的邏輯。其算法的具體描述為：假設m行n列的矩陣A和r行v列的矩陣B相乘得到矩陣C，則首先矩陣A和矩陣B必須滿足n=r，也就是說，第一個矩陣的列數必須和第二個矩陣的行數相同。在運算時，第一個矩陣A的第i行的所有元素同第二個矩陣B第j列的元素對應相乘，並把相乘的結果相加，最終得到的值就是矩陣C的第i行第j列的值。

這個過程用數學公式描述為：

C(i，j)=A(i1，i2，i3……in)×B(j1，j2，j3……jv)

進而推出：

C(i，j)= i1×j1+i2 ×j2+i3×j3……+in×jv

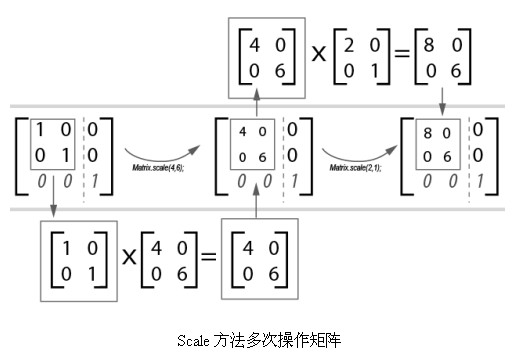
從矩陣的乘法運算過程可以看出，矩陣A和矩陣B相乘的產生的矩陣C，必然是m行v列的。例如，一個5×3的矩陣同一個3×7的矩陣相乘，結果必然是產生一個5×7的矩陣。而一個5×3的矩陣同一個5×7的矩陣，則無法相乘。圖演示了兩組矩陣的乘法運算。

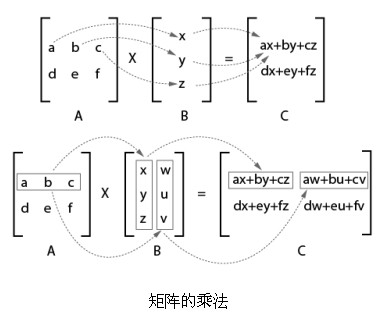
在圖形變換時，經常用到多次變換，這會造成多個矩陣相乘。如果多個矩陣相乘，則等價於前兩個矩陣相乘的結果再乘以第三個矩陣，以此向後類推。例如，假設ABCD都是矩陣，則A×B×C×D=((A×B)×C)×D。矩陣乘法同數字乘法不同，其運算的先後順序十分敏感，矩陣A乘矩陣B的結果可能完全不同於矩陣B乘矩陣A的結果，有時甚至根本無法相乘。