矩陣分析-基礎-常見矩陣

單位陣（Identity Matrix）

定義：單位陣是對角元素為1，其它元素為0的方陣。

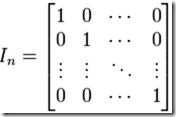，也可表示為I_n = diag(1,1,...,1)

性質：

AI_n = A 且 I_nB = B

對稱陣（symmetric matrix）

定義：對稱陣為其轉置和自身相等的方陣，即元素以主對角線（（左上至右下）為軸進行對稱，A^T = A

斜對稱陣（skew-symmetric matrix）

定義：對稱陣為其轉置和自身加法逆相等的方陣，A^T = − A。

性質：

• • • 1）斜對稱矩陣自身相乘的積是對稱矩陣。
    • 2）任意矩陣A，A^T − A是斜對稱矩陣。
    • 3）若A是斜對稱矩陣，x是向量，x^TAx = 0
    • 4）斜對稱矩陣的主對角線元素必是零，所以其跡數為零。

初等矩陣（Elementary Matrix）

接近問題時，常將復雜問題分解為一些基礎模塊。這裡要介紹的就是如何將一個矩陣分解為一系列初等矩陣的乘積。

定義：一個 n 階單位矩陣 E 經過一次初等行變換或一次初等列變換所得矩陣稱為 n 階初等矩陣。

初等矩陣分為3種類型，分別對應著3種不同的行/列變換。

1）類型1，互換行/列：  。如下互換第 i,j行 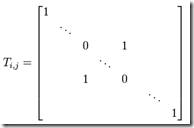                                        2）類型2，把某行/列乘以一非零常數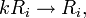：  其中  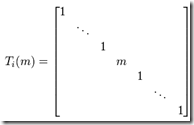                                     3）類型3，把第  i 行（列）加上第  j 行（列）的  k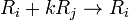  倍：                                     

性質：

• 1）；| T_ij | = − 1； | T_ijA | = − | A | 。
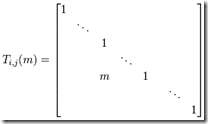
  • 2），此矩陣及其逆矩陣均為對角矩陣；|T_i(m) | = m， | T_i(m)A | = m | A | 。
    • 3） T_ij(m) ^{− 1} = T_ij( − m)，此矩陣及其逆矩陣均為三角矩陣；| T_ij(m) | = 1， | T_ij(m)A | = | A | 。

作用：左乘初等矩陣相當於對矩陣行進行初等變換；右乘初等矩陣相當於對矩陣列進行初等變換。