矩陣分析-線性系統-1 定義、方程組解的表現形式和性質

本文主要是介绍矩陣分析-線性系統-1 定義、方程組解的表現形式和性質，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

http://www.cnblogs.com/pegasus/archive/2011/07/31/2121792.html

1. 定義

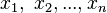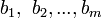線性系統（線性方程組）的一般形式如下，其中 $x_1,\ x_2,...,x_n$ 是未知數, $a_{11},\ a_{12},...,\ a_{mn}$ 是系數, $b_1,\ b_2,...,b_m$ 是常量。

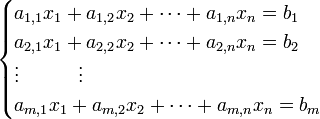
$\begin{cases}a_{1,1}x_{1} + a_{1,2}x_{2} + \cdots + a_{1,n}x_{n}= b_{1} \\ a_{2,1}x_{1} + a_{2,2}x_{2} + \cdots + a_{2,n}x_{n}= b_{2} \\ \vdots \quad \quad \quad \vdots \\ a_{m,1}x_{1} + a_{m,2}x_{2} + \cdots + a_{m,n}x_{n}= b_{m} \end{cases}$

線性方程組的列向量形式如下。從這個角落來看，常量b是系數列向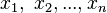量{a1,a2…,an}基於未知數 $x_1,\ x_2,...,x_n$ 的加權線性組合（linear combination）。這讓我們能夠利用向量空間（vector spaces）理論來分析問題。例如，系數列向量{a1,a2…,an}所有線性組合的集合稱為它們張成的空間。如果在這個空間上僅有唯一的線性組合，那麼這個方程有唯一解。

$x_1 \begin{bmatrix}a_{11}\\a_{21}\\ \vdots \\a_{m1}\end{bmatrix} + x_2 \begin{bmatrix}a_{12}\\a_{22}\\ \vdots \\a_{m2}\end{bmatrix} + \cdots + x_n \begin{bmatrix}a_{1n}\\a_{2n}\\ \vdots \\a_{mn}\end{bmatrix} = \begin{bmatrix}b_1\\b_2\\ \vdots \\b_m\end{bmatrix}$

線性方程組的矩陣形式 $A\bold{x}=\bold{b}$ 。The number of vectors in a basis for the span is now expressed as the rank of the matrix.

$A=\begin{bmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\a_{21} & a_{22} & \cdots & a_{2n} \\\vdots & \vdots & \ddots & \vdots \\a_{m1} & a_{m2} & \cdots & a_{mn}\end{bmatrix},\quad\bold{x}=\begin{bmatrix}x_1 \\x_2 \\\vdots \\x_n\end{bmatrix},\quad\bold{b}=\begin{bmatrix}b_1 \\b_2 \\\vdots \\b_m\end{bmatrix}$

2. 方程組的解

2.1 幾何解釋

對於兩個變量（x 和 y) 的系統，每個線性等式對應xy-平面上的一條線，線上的點滿足此線性公式。對於這個線性系統（線性方程組），它的解必須滿足所有線性公式，因此它的解是所有線的交集，從而有三種情況：1）交集是一個點，有唯一解；2）是一條直線，有無窮個解；3）是空集，不存在解。

當有3各變量時，每個線性方程對於一個三維空間上的面。當有n各變量時，每個線性方程對於一個n維空間上的超平面。

圖.2變量-2線性公式-唯一解圖。3變量-2線性公式-無窮解

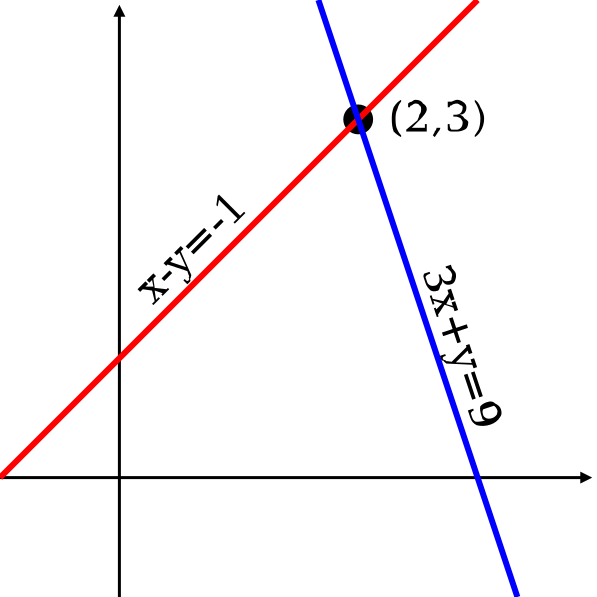
2.2 解的表現形式

線性方程組的表現取決於方程組個數和未知數個數：

1）通常，方程個數m<未知數個數n時，有無窮多解，在某些情況下有唯一洗漱解（感知壓縮，Compressed Sensing)。這樣的系統稱為欠定系統（underdetermined system）

2）通常，方程個數m=未知數個數n時，有唯一解。這樣的系統稱為恰定系統。

3）通常，方程個數m>未知數個數n時，沒有解。這樣的系統稱為超定系統（overdetermined system）。