本文主要是介绍矩陣變形方法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
http://blog.csdn.net/as3_flash/article/details/2378571
用戶在代碼中可以創建矩陣類的實例,並通過手動設置矩陣的內部屬性a、b、c、d、tx和ty,純手工的創造或改變一個變換矩陣。如果用戶具備豐富的圖形學知識,可以自己算出位移,縮放,旋轉,斜切等變形所需要的二次變換矩陣值,那麼使用這種方法就足夠了。高級用戶使用這種方式將會相當的高效。
但是,顯然大多數用戶並不瞭解矩陣數學和計算機圖形學算法。對它們而言,直接操作Matrix類的屬性是很不容易的。所以為了簡化用戶操作,AS3中的Matrix類綁定了一些內部方法。初級用戶完全可以不顧及矩陣數學和圖形學算法,通過使用這些內建的方法,修改它們的參數,累加它們的效果,最終得到想要的結果。
表所示為AS3中Matrix類內建的變形方法:
表Matrix類內建變形方法
| 名稱 | 詳情 |
| translate(tx, ty) | 實現顯示對象的移動。 其中的tx,ty描述的是顯示對像移動的差值,而不是目標點的最終坐標。 |
| scale(sx, sy) | 實現顯示對象的放大和縮小。 sx:倍數,對應x坐標。 sy:倍數,對應y坐標。 |
| rotate(q) | 旋轉一個對象的 q:對象的旋轉量。這是一個弧度值。 |
為了瞭解矩陣類的實際使用,下面介紹一個最簡單的實例。新建AS3項目,在代碼編輯器中直接輸入以下代碼:
var myMatrix:Matrix=new Matrix;
trace(myMatrix.toString());
//使用translate()方法修改矩陣
myMatrix.translate(5,13);
trace(myMatrix.toString());
//新建一個點
var myp:Point=new Point(5,5);
trace(myp.toString());
//新建一個目標點,用於接受位移後的坐標
var mypt:Point;
//應用位移矩陣
mypt=myMatrix.transformPoint(myp);
//輸出目標點的坐標
trace(mypt.toString());
以上代碼較為簡單,註釋也很清楚,不再贅述。運行這段代碼,可以得到輸出:
(a=1, b=0, c=0, d=1, tx=0, ty=0)//初始變換矩陣
(a=1, b=0, c=0, d=1, tx=5, ty=13)//修改後的變形矩陣
(x=5, y=5)//原坐標
(x=10, y=18)//目標坐標
至此,矩陣類的運行流程就很清楚了。聲明一個矩陣類就建立了一個初始變換矩陣,初始矩陣如圖所示:
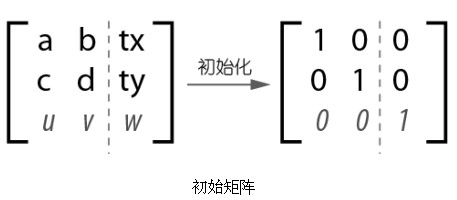
使用矩陣類的方法其本質是修改這個初始矩陣,應用矩陣類其實就是用該變形矩陣代入仿射變形公式進行運算的過程。
有的用戶覺得這些方法使用起來並不方便,因為它們都是相對值。例如,其中的translate(tx,ty)方法,並不能將對像直接移動到目標點,其真實作用是在水平方向上移動tx距離,在垂直方向上移動ty距離。如果想把顯示對像移動到某點,用戶必須自己進行計算前後的距離差。
其實這是矩陣的內部機製造成的。Matrix類的這些方法都是基於矩陣操作的,遵循的是數學思維。當用戶使用translate(tx,ty)方法時,本質上構建一個產生位移的數學矩陣。矩陣提供了一種仿射變形的映射。AS3執行時,將這個矩陣應用在顯示對像內部的每一個點,令它們在水平方向上移動tx距離,在垂直方向上移動ty距離。假設能夠指定最終的目標值,則運算後,顯示對象的每一個點都會被映射到這同一個點,則顯示對象就被扭曲壓縮了,這顯然是不正確的。
如果用戶從人的思維去考慮,覺得這些內建方法不方便,可以自己寫一組自定義函數,擴展它們的功能。
这篇关于矩陣變形方法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



