相关文章
Codeforces Round #113 (Div. 2) B 判断多边形是否在凸包内
题目点击打开链接 凸多边形A, 多边形B, 判断B是否严格在A内。 注意AB有重点 。 将A,B上的点合在一起求凸包,如果凸包上的点是B的某个点,则B肯定不在A内。 或者说B上的某点在凸包的边上则也说明B不严格在A里面。 这个处理有个巧妙的方法,只需在求凸包的时候, <= 改成< 也就是说凸包一条边上的所有点都重复点都记录在凸包里面了。 另外不能去重点。 int
【Godot4.3】多边形的斜线填充效果基础实现
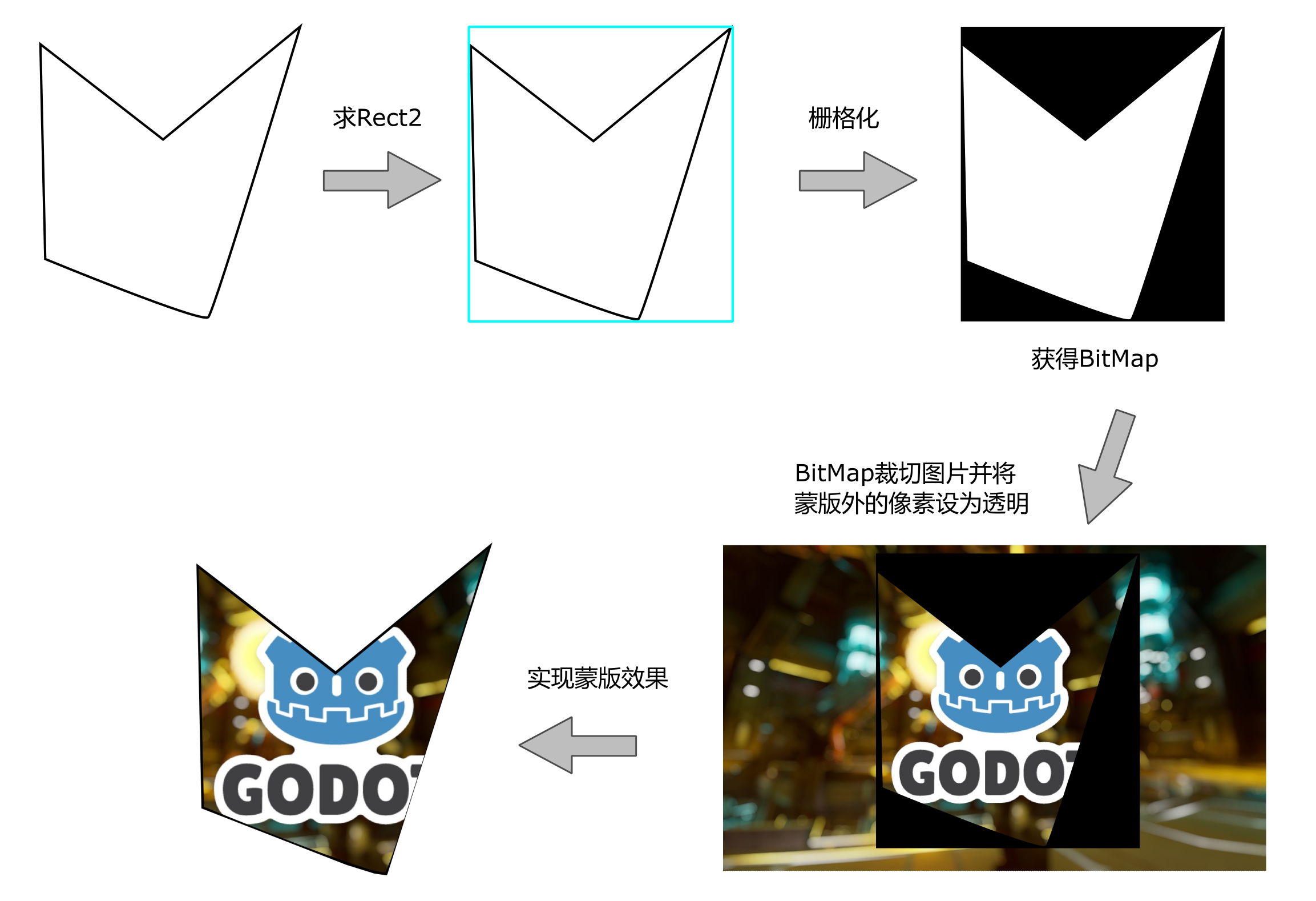
概述 图案(Pattern)填充是一个非常常见的效果。其中又以斜线填充最为简单。本篇就探讨在Godot4.3中如何使用Geometry2D和CanvasItem的绘图函数实现斜线填充效果。 基础思路 Geometry2D类提供了多边形和多边形以及多边形与折线的布尔运算。按照自然的思路,多边形的斜线填充应该属于“多边形与折线的布尔运算”范畴。 第一个问题是如何获得斜线,这条斜线应该满足什么样
代码随想录刷题day25丨491.递增子序列 ,46.全排列 ,47.全排列 II
代码随想录刷题day25丨491.递增子序列 ,46.全排列 ,47.全排列 II 1.题目 1.1递增子序列 题目链接:491. 非递减子序列 - 力扣(LeetCode) 视频讲解:回溯算法精讲,树层去重与树枝去重 | LeetCode:491.递增子序列_哔哩哔哩_bilibili 文档讲解:https://programmercarl.com/0491.%E9%80%92%E
模拟退火判断一个圆是否可以放在一个多边形内
/*给定n个点的一个多边形,一个圆的半径,判断圆是否可以放在多边形里*//* ***********************************************Author :rabbitCreated Time :2014/7/3 22:46:38File Name :2.cpp**********************************************
天然药物化学史话:“四大光谱”在天然产物结构鉴定中的应用-文献精读46
天然药物化学史话:“四大光谱”在天然产物结构鉴定中的应用,天然产物化学及其生物合成必备基础知识~ 摘要 天然产物化学研究在药物研发中起着非常重要的作用,结构研究又是天然产物化学研究中最重要的工作之一。在天然药物化学史话系列文章的基础上,对在天然产物结构研究中起绝对主导作用的“四大光谱”分析技术,即红外光谱、紫外光谱、质谱、核磁共振波谱在天然产物结构鉴定中的应用历史进行回顾与总结,并对其发展
利用向量积(叉积)计算三角形的面积和多边形的面积(hdu2036)
开始撸计算几何题目了。。。。。。。 预备知识:叉乘求多边形面积 参考证明资料: 公式证明: http://www.cnblogs.com/xiexinxinlove/p/3708147.html 高中知识: http://wenku.baidu.com/view/867e6edfad51f01dc281f11a.html #include<stdio.h>#inclu
HDU 2036 求多边形面积
题目: http://acm.hdu.edu.cn/showproblem.php?pid=2036 对用(按逆时针排列)描述的多边形,其面积为: 若按顺时针排列,取负数即可。 资料链接: http://zh.wikipedia.org/wiki/%E5%A4%9A%E8%BE%B9%E5%BD%A2 不知道这公式是咋推导的,网上找不到,先留着。 #
图形几何-如何将凹多边形分解成若干个凸多边形
凹多边形的概念 凹多边形是指至少有一个内角大于180度的多边形。与之相对,凸多边形的所有内角均小于或等于180度,且任意两点之间的连线都完全位于多边形内部。将凹多边形分解成若干个凸多边形是计算几何中的一个重要问题。 分解原理 将凹多边形分解为凸多边形的基本原理是通过绘制对角线来消除凹角。对角线是连接多边形两个非相邻顶点的线段。通过适当选择对角线,可以将凹多边形
LeetCode 46 Permutations + LeetCode 47 Permutations II
题意: 给出一串(46题)不重复or(47题)有重复的数字,要求输出所有排列。 思路: 有没有重复不影响思路 = =。 代码展示为46题提交结果,47题一样过…… 可以偷懒用next_permutation方法也可以自己实现,实现方法为从后往前找第一个出现的nums[i] < nums[i+1],从i后面找出比nums[i]稍大一点的数字nums[x],交换nums[i]和nums[
[C++11#46](三) 详解lambda | 可变参数模板 | emplace_back | 默认的移动构造
目录 一.lambda 1. 捕捉列表 2. 底层原理 二. 可变参数模板 1. 递归函数方式展开参数包 2. 数组接收方式展开参数包 3. 运用 4.emplace_back 5.移动构造和拷贝构造 强制生成 default 一.lambda 可调用类的对象 函数指针--少用 void(*ptr) (int x) 仿函数--构造类 重载 operator() 对象






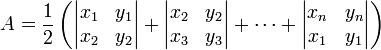


 详解lambda | 可变参数模板 | emplace_back | 默认的移动构造](https://img-blog.csdnimg.cn/img_convert/2c89392ac4a0c9dbd279183dbda3d2bc.png)