本文主要是介绍【点云系列】LPD-Net: 3D Point Cloud Learning for Large-Scale Place Recognition and Environment Analysis,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 1. 简介
- 2. 动机
- 3. 方法
- 整体网络架构
- Adaptive Local Feature Extraction模块:
- Feature Transformation:
- 基于图的聚合模块:
- 4. 实验
- 实验效果:
- 消融实验
- 5. 参考
1. 简介
一句话介绍:相比较PointNetVLAD,包含了传统局部特征编码+基于学习的局部编码。
会议:ICCV 2019
论文:https://openaccess.thecvf.com/content_ICCV_2019/papers/Liu_LPD-Net_3D_Point_Cloud_Learning_for_Large-Scale_Place_Recognition_and_ICCV_2019_paper.pdf
代码:https://github.com/Suoivy/LPD-net
2. 动机
针对局部特征提取,采用 自适应局部特征提取模块+ 基于图的邻居聚合模块
直接基于原始3D点云提取具有区分性和泛化性的全局特征。
3. 方法
整体网络架构
包括三个部分:
- 特征提取模块。其实就是加了 Local Feature Extraction部分进行了拼接。
- 基于图的邻居聚合模块。 基于DGCNN,动态图的构建。
- NetVLAD特征编码模块,与PointNetVLAD当中的NetVLAD一样。

Adaptive Local Feature Extraction模块:
考虑到对于每个点的局部3D结构,会计算其最近的k个邻近点的影响。因此使用3D位置协方差矩阵来作为局部结构张量。
不失一般性的,假设这个对称的正定协方差矩阵有3个特征值:
λ 1 i ≥ λ 2 i ≥ λ 3 i ≥ 0 \lambda^i_1 \geq \lambda^i_2 \geq \lambda^i_3 \geq 0 λ1i≥λ2i≥λ3i≥0。
那么根据[24],可以通过香浓熵理论的某个方面来描述局部结构的不确定性:
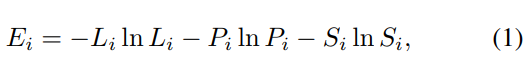
其中, L i = λ 1 i − λ 2 i λ 1 i L_i = \frac{\lambda^i_1 - \lambda^i_2}{\lambda^i_1} Li=λ1iλ1i−λ2i, P i = λ 2 i − λ 3 i λ 1 i P_i =\frac{\lambda^i_2 - \lambda^i_3}{\lambda^i_1} Pi=λ1iλ2i−λ3i, S i = λ 3 i λ 1 i S_i=\frac{\lambda^i_3}{\lambda^i_1} Si=λ1iλ3i 分别代表 每个点对应局部邻域的共线,共面,散射特征,这些特征分别描述了点 i i i的 1维、2维、和3维的局部结构。
由于点云当中点的分布是均匀的,我们通过最小化 E i E_i Ei每个点的临近点来确定出最优的邻居点:
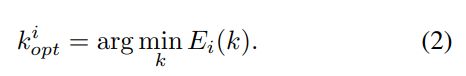
适合描述大场景下的局部特征可以描述为以下四类:
- 基于特征值的3D特征( F 3 D F_{3D} F3D)
- 来自于3D点云到水平面的映射特征( F 2 D F_{2D} F2D)
- 法向量( F V F_V FV)
- 基于直方图统计Z-axis satistics( F z F_z Fz)
根据[24]证明到
F 3 D F_{3D} F3D、 F V F_V FV以及 F z F_z Fz对于大场景3D场景分析问题非常有效;
F 2 D F_{2D} F2D与 F Z F_Z FZ对于自动驾驶类人物当中的大场景定位问题非常有效;
本文当中,考虑到特征的冗余性与可区分性,为每个点选取了一下10个局部特征来描述局部分布和结构信息:
-
F 3 D F_{3D} F3D特征:
曲率变化 C i = λ 3 i ∑ j = 1 3 λ j i C_i=\frac{\lambda^i_3}{\sum^3_{j=1} \lambda^i_j} Ci=∑j=13λjiλ3i,
Omni方差 O i = ∏ j = 1 3 λ j i 3 ∑ j = 1 3 λ j i O_i=\frac{\sqrt[3]{\prod^3_{j=1}\lambda^i_j}}{\sum^3_{j=1}\lambda^i_j} Oi=∑j=13λji3∏j=13λji,
共线 L i = λ 1 i − λ 2 i λ 1 i L_i = \frac{\lambda^i_1 - \lambda^i_2}{\lambda^i_1} Li=λ1iλ1i−λ2i,
特征值熵 A i = − ∑ j = 1 3 ( λ j i l n λ j i ) A_i=-\sum^3_{j=1}(\lambda^i_j ln\lambda^i_j ) Ai=−∑j=13(λjilnλji),
局部点的密度 D i = k o p t i 4 3 ∏ j = 1 3 λ j i D_i=\frac{k^i_{opt}}{\frac{4}{3} \prod^3_{j=1} \lambda^i_j} Di=34∏j=13λjikopti -
F 2 D F_{2D} F2D特征:
2D散射特征: S i , 2 D = λ 2 D , 1 i + λ 2 D , 2 i S_{i,2D}=\lambda^i_{2D,1}+\lambda^i_{2D,2} Si,2D=λ2D,1i+λ2D,2i
2D线性特征: L i , 2 D = λ 2 D , 2 i λ 2 D , 1 i L_{i,2D}= \frac{\lambda^i_{2D,2}}{\lambda^i_{2D,1}} Li,2D=λ2D,1iλ2D,2i,这里的 λ 2 D , 1 i \lambda^i_{2D,1} λ2D,1i与 λ 2 D , 2 i \lambda^i_{2D,2} λ2D,2i表示2D协方差矩阵对应的特征值 -
F V F_V FV特征:
法向量 V i V_i Vi的垂直分量 -
F Z F_Z FZ特征:
最大高度残差: △ Z i , m a x \triangle Z_{i,max} △Zi,max
高度变量: σ Z i , v a r \sigma Z_{i,var} σZi,var
Feature Transformation:
包括三种结构来体现局部特征间的关联性:如图3所示
- FN-原始结构: 两路输出分别是特征 f F f_F fF与使用KNN在 f F f_F fF上操作的其近邻关系 F R F_R FR
- FN-串联结构:两路输出分别是:经过Transform Net[11]的特征 f F T f_{FT} fFT与其KNN最近邻 f R T f_{RT} fRT
- FN-并行结构:两路输出分别是: 特征 f F f_F fF与其近邻关系 f R T f_{RT} fRT(与FN-串联结构中的同)。
消融实验验证了,FN-并行结构是最好的。

基于图的聚合模块:
与物体级别的点云不同,3D大场景中总是包括几类局部结构:面、角、边等,且具有相似的局部结构。因此采用基于图神经网络来聚合关联性,如下图4所示。

特征聚合: 特征空间与笛卡尔坐标空间。如下图5所示:
特征空间:
- 对每个点 i i i通过多次KNN迭代,构建动态图 G i , d G_{i,d} Gi,d,可以简单看成DGCNN。
- 其中边的定义为 e i j m = p i − p j m , m = 1 , 2 , . . . k . e^m_{ij}=p_i - p^m_j,m=1,2,... k. eijm=pi−pjm,m=1,2,...k.
- MLP:更新边关联性
- 最大池化:聚合k个边属性到一个特征点上 p i p_i pi。
- 由于基于图特征的学习,因此 两个点的特征+笛卡尔空间的距离可以聚合起来 捕获相似的语义信息,说的什么意思呢,就是基于图的局部结构可以表达局部语义信息。

聚合结构如图6所示,3种模式:
- 平行拼接: 特征+ 关联性
- 平行最大池化拼接: max(特征+关联性)
- 串联拼接: 关联性由聚合后的特征获取
实验表明,串联拼接效果最好。

4. 实验
实验效果:
效果比之前的缺失好很多

确实耗时

消融实验
看上去adaptive的k确实是最好的

这个消融实验是为了说明选取不同框架的效果,可以看到用 串联模式FN-SF是最佳的。
而特征关联性则是并联效果比较好。


5. 参考
暂无
这篇关于【点云系列】LPD-Net: 3D Point Cloud Learning for Large-Scale Place Recognition and Environment Analysis的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






