多核实时调度—多项式时间复杂度最优任务分配算法PTAS解读

本文主要是介绍多核实时调度—多项式时间复杂度最优任务分配算法PTAS解读，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

PTAS 是针对多核分区调度的，最初的那篇论文，是提出了一个分配思想，而没有指定分区调度中具体是采用固定优先级调度和动态优先级比如EDF调度。然后后面一个论文就将其具体化，且高效实现了，该文章的算法过程如下。

针对periodic任务，在每个核上采用EDF调度，是一种可以以 $\varepsilon$ 误差接近理论最优的实时任务分配算法，其中 $\varepsilon$ 是一个我们人为指定的常数，最牛逼的是，该算法在运行时可以以多项式复杂度时间得到以 $\varepsilon$ 为误差的最优分配结果。该论文理解起来还是很有难度的。该方法的实现过程如下：首先指定 $\varepsilon$ （下面我们的分析用字母e代替了），然后穷举法生成所有可行的分配表（2的n次方这样的指数时间复杂度），然后运行时（比如实时操作系统正在运行了）查找匹配该分配表，从而得到分配结果。

详细过程如下：

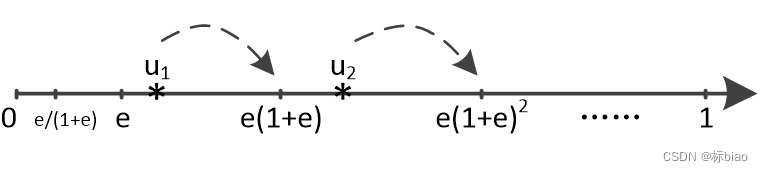
离散化利用率0-1的所有到区间：(e/(1+e), e]，(e, e(1+e)]，(e, e(1+e)^2]，.....。然后所有利用率点ui都会取所在区间的右端点值，也就是round up（或者叫做modified）。这样之后可能存在的利用率点仅为：e，e(1+e)，e(1+e)^2，......。总共有多少个利用率点呢，这个可以算的，我们记为|V(e)|。我们会发现后一个利用率值除以前一个都等于(1+e)，而且利用点的个数和人为指定的常数e都是有关系的，所以叫做人为指定误差嘛。很明显，如果是单核，能容纳的最多任务为1/e个了。
这样我们就可以把一个任务集n个任务的利用率分配情况给穷举出来了。
比如e=0.4（我们计算出只有3个利用率点，0.4, 0.56, 0.784，因此|V(e)|=3）。那么对于每个核，我们都能穷举出所有可能的利用率存在方式，表示为有序对（下面会介绍），比如<2,0,0>,<1,1,0>,<0,0,1>,<0,1,0>，其中<2,0,0>表示0.4利用率处可以有2个0.4利用率，但是0.56处和0.784处都不能有该点利用率的任务了，因为加起来大于1了，就不可调度了。这些合法有序对为，<2,0,0>,<1,1,0>,<1,1,0>,<0,0,1>,<0,1,0> ，其中<1,0,0>这个就叫做非最大有序对（或者说非饱和），因为该有序对再加入一个0.4利用的任务，照样还是可调度的。所以最大有序对意思是再加入一个e利用率的任务，就不可调度了。处理器只有一个核的情况，最大有序对表述为( 构造的时间复杂度为1/e为指数的 )
L1(e)={ <2,0,0>,<1,1,0>,<0,0,1>,<0,1,0> }，用z1表示某个有序对的编号，也叫ID。
多核情况下，每个核都用这个表示即可，因为是同构多核。

用户给定输入3个任务，它们的利用率{0.3，0.35，0.55}，利用率转换（叫做modified）后为{0.4，0.4，0.56}，表示为下面要说的有序对，就是<2,1,0>（这个是输入的），该任务集在两个核上的分配，就会有很多种情况，其中可行的分配方式只有下面2种而已（每个核上利用率小于1该核即可调度）。因此我们可以用一个有序对来表示分配结果<x1，x2，...，xi，...，x|V(e)|>，这里的|V(e)|是作为x的下标。xi表示分配在e(1+e)^i这个利用率点的任务数。这个例子中，分配方法1，对于核1，就是<2,0,0>，对于核2，就是<0,1,0>。分配方法2，对于核1，就是<1,1,0>，对于核2，就是<1,0,0>。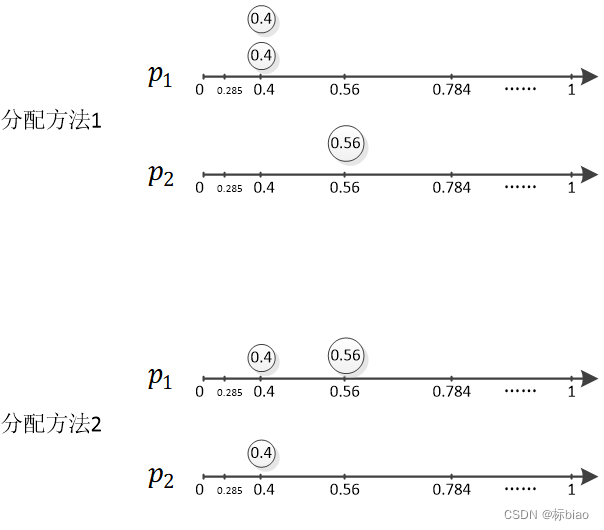

如果是2个核，最大化该如何表述呢，首先肯定是针对一个目标有序对<y1,y2,...y|V(e)|>，此时该有序对就是这2个核所能容纳下的最大利用率了，任意添加一个小的e利用率进去，都会导致分配失败（构造这样，时间复杂度|L1(e)|^m）。那么很明显，这个最大化的有序对，分配在两个核上，每个核也处于最饱和状态了，即每个核的最大有序对里挑出来一个呗，那上面的z1就是核1上挑出来的有序对的编号，z2，就是核2上挑出来的有序对的编号。因此形式化表述为：
(<y1,y2,...,y|V(e)|>)，<z1,z2,...,zm>），m为核数。

Lm(e)={ (<y1,y2,...,y|V(e)|>)，<z1,z2,...,zm>），(<y1’,y2’,...,y‘|V(e)|>)，<z1’,z2‘,...,zm’>），......, }。构建的查找表

上面例子表述为：
L2(e)={(<4,0,0>)，<1,1>），(<3,1,0>)，<1,2>），(<3,0,1>)，<1,3>）}，这个就是PTAS算法在运行前预处理时构建的查找表

上面的意思是，假如对于<4,0,0>这个是round up后的目标任务集，表示有4个0.4利用率的任务，那这个有序对为什么是2核处理器中最大有序对呢，因为你随便再给一个利用率（0.4，0.56.0.784这几个随便给一个），都会分配失败。这个分配结果就是每个核都在0.4那儿分配两个就行了，也就是核1：<2,0,0>，核2也是：<2,0,0>，查询上面L1(e)的表达式可知，编号都是1的有序对，因此表示为<z1,z2>为<1,1>。同理(<3,1,0>)，<1,2>）也是这么得来的。

我们会发现这样一个性质，就是待分配最大化有序对的每个分量成员，就是每个核最大化有序对对应分量求和需要相等，比如(<4,0,0>)，<1,1>）中的4，在核1中是2，核2中也是2，加起来就是4了。那么如果现在用户给一个任务集，表示为了<3,0,0>有序对，问我们能不能分配成功，当然可以，因为我们能找到预处理时候上面构造的查找表，和查找表中的<4,0,0>相匹配，发现每个分量只要小于等于查找表中的<4,0,0>的每个分量，则该<3,0,0>有序对就可以分配成功，就用对应的<1,1>这个分配方式即可，即核1分配两个0.4利用率的任务，核2就只分配剩下的一个就行了（虽然最饱满的情况是可以分2个0.4的）。
终于解释完了上面的最大有序对，其实分配的过程就是，预先建立好查找表Lookup table，从上面直到为1/e为指数的时间复杂度的，但是没关系，这个是系统运行前预处理阶段完成的，然后运行阶段，任意给一个任务集，只需要进行round up修改为有序对，然后和查找表中的进行匹配（就是每个分量都小于查找表中某个有序对即可，这个匹配过程是多项式时间复杂度的），然后就能知道分配成功或者失败了，成功也能知道具体如何分配核的了。
真正的运行时阶段，就是多项式时间复杂度而已，这就PTAS分配算法名字的由来。

（当然PTAS算法还考虑了有些任务利用率小于e/(1+e)的情况，这个最后分配即可，看看哪个核能放下就分配即可）

总结： PTAS分配算法确实做到了多项式时间复杂度的可指定精度（和理论最优分配算法的差距）的分配，但是该算法构建查找表因为还是有点复杂（不吃透这个算法原理就没法弄），而查找表会占用很多的内存空间，因此该算法实际系统中用到的不多，但是这个方法很有启发意义，空间换时间。实际实时系统中用得较多的是启发式分配算法（虽然不能最优，但是可以很接近最优，而且实现简单，不需要占什么内存，时间复杂度也低，而且还有个重要的点：PTAS不能适应任务动态加入的情况，而启发式算法（也叫近似算法）则可以比如FF），比如FF,NF,WF,BF等，下个博客就讲解这几个算法。

多核实时调度—任务分配启发式算法解读_标biao的博客-CSDN博客

这篇关于多核实时调度—多项式时间复杂度最优任务分配算法PTAS解读的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！