day41| 01背包问题一 01背包问题二（滚动数组篇）416. 分割等和子集 1049.最后一块石头的重量II 494. 目标和 474. 一和零

本文主要是介绍day41| 01背包问题一 01背包问题二（滚动数组篇）416. 分割等和子集 1049.最后一块石头的重量II 494. 目标和 474. 一和零，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

由于笔试的时候会判重，而这里面的代码都是我自己写的，所以以后的博客都要求会员才能看，感谢理解

背景介绍

01背包问题一

01背包问题：有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。
暴力求解
每一件物品其实只有两个状态，取或者不取，所以可以使用回溯法搜索出所有的情况，那么时间复杂度就是$o(2^n)$，这里的n表示物品数量。

所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化！

思路

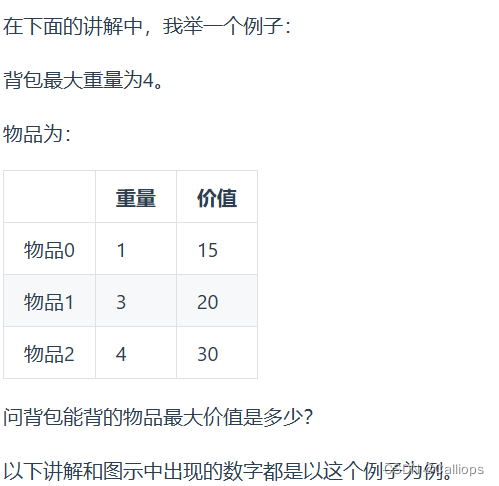
依然动规五部曲分析一波。

1. ❤️确定dp数组以及下标的含义
   对于背包问题，有一种写法， 是使用二维数组，即dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。
2. ❤️确定递推公式
   
3. dp数组如何初始化
   首先从dp[i][j]的定义出发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。
   纵向初始化：dp[0][j]，即：i为0，存放编号0的物品的时候，各个容量的背包所能存放的最大价值。
   那么很明显当 j < weight[0]的时候，dp[0][j] 应该是 0，因为背包容量比编号0的物品重量还小。
   当j >= weight[0]时，dp[0][j] 应该是value[0]，因为背包容量放足够放编号0物品。
   
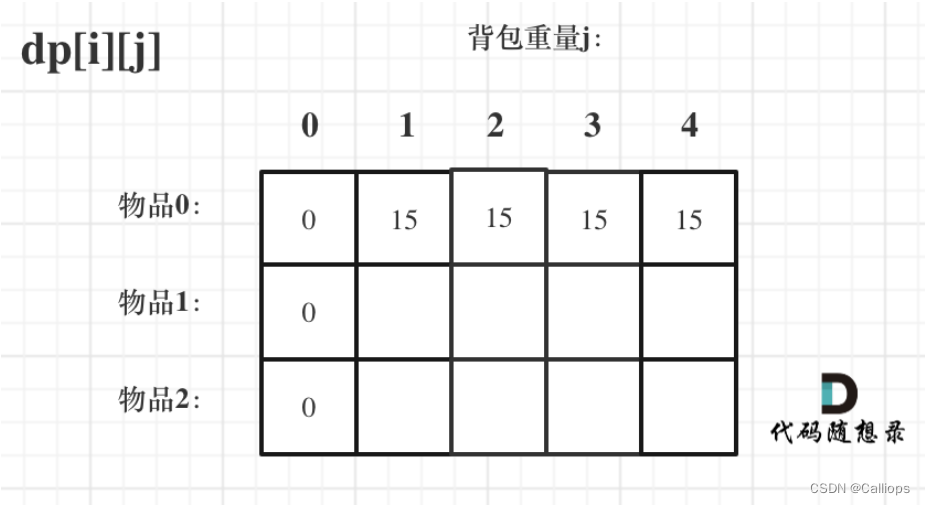
   这里还讲了一个其他位置的初始化：任意都可以，因为都会被覆盖
4. 遍历顺序：两层for循环，
   先遍历 物品还是先遍历背包重量呢？
   其实都可以！！ 但是先遍历物品更好理解。
   

方法一

自己写的注意事项：

1. 一开始没有完全理解，dp二维数组的列数是bagweight，而不是len(weight)
2. 写代码的时候一定是bagweight+1啊，因为bagweight是必须要算在里面的
3. 此外，卡吗网输入的都是str类型要注意哦

def test_2_wei_bag_problem1(weight, value, bagweight):# 二维数组dp = [[0] * (bagweight + 1) for _ in range(len(weight))]# 初始化for j in range(weight[0], bagweight + 1):dp[0][j] = value[0]# weight数组的大小就是物品个数for i in range(1, len(weight)):  # 遍历物品for j in range(bagweight + 1):  # 遍历背包容量if j < weight[i]:dp[i][j] = dp[i - 1][j]else:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])return dp[len(weight) - 1][bagweight]if __name__ == "__main__":weight = [1, 3, 4]value = [15, 20, 30]bagweight = 4result 

这篇关于day41| 01背包问题一 01背包问题二（滚动数组篇）416. 分割等和子集 1049.最后一块石头的重量II 494. 目标和 474. 一和零的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---