本文主要是介绍洛谷 P3379:最近公共祖先(LCA)← RMQ+欧拉序,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
【题目来源】
https://www.luogu.com.cn/problem/P3379
【题目描述】
如题,给定一棵有根多叉树,请求出指定两个点直接最近的公共祖先。
【输入格式】
第一行包含三个正整数 N,M,S,分别表示树的结点个数、询问的个数和树根结点的序号。
接下来 N−1 行每行包含两个正整数 x,y,表示 x 结点和 y 结点之间有一条直接连接的边(数据保证可以构成树)。
接下来 M 行每行包含两个正整数 a,b,表示询问 a 结点和 b 结点的最近公共祖先。
【输出格式】
输出包含 M 行,每行包含一个正整数,依次为每一个询问的结果。
【输入样例】
5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5
【输出样例】
4
4
1
4
4
【说明/提示】
对于 30% 的数据,N≤10,M≤10。
对于 70% 的数据,N≤10000,M≤10000。
对于 100% 的数据,1≤N,M≤500000,1≤x,y,a,b≤N,不保证 a≠b。
【算法分析】
● 一般来讲,求 LCA 有 3 种常见方法:倍增、RMQ+欧拉序、tarjan(离线)。本题代码介绍“RMQ+欧拉序”法求LCA。
● 欧拉序:https://blog.csdn.net/hnjzsyjyj/article/details/139681246
欧拉序有常见的两种情况。下图是适用于求 LCA 的第一种情况的欧拉序。由图可知,此图的第一种情况的欧拉序为:1,2,3,4,3,5,3,6,3,2,7,2,1,8,9,8,1。
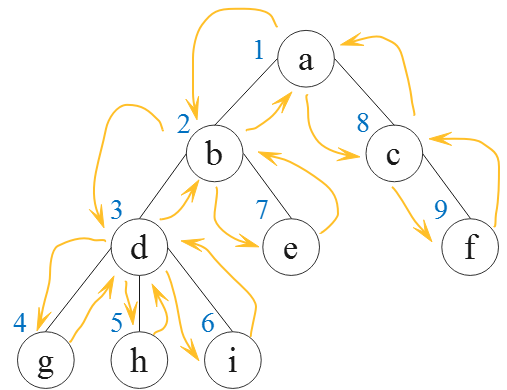
第一种情况的欧拉序具有如下性质:即若设 first[u] 是欧拉序中某结点 u 第一次出现的位置,first[v] 是欧拉序中某结点 v 第一次出现的位置,树上两结点 u, v 的最近公共祖先(LCA),为欧拉序区间 [first[u], first[v]] 或 [first[v], first[u]] 中时间戳最小的结点。其中,某结点的时间戳可以理解为第一次 DFS 遍历到该结点的顺序。 据此性质,易知利用欧拉序求 LCA,本质上就是一个 RMQ 问题。而 RMQ 问题常用 ST 算法来初始化数据。
● ST 算法:https://blog.csdn.net/hnjzsyjyj/article/details/103429761
ST算法(Sparse Table,稀疏表)主要用于解决区间最值问题(即RMQ问题)。因为ST算法求解RMQ问题时的时间复杂度只有O(nlogn),查询时间复杂度为常数阶O(1),所以我们还常称ST算法为TLE的死敌。虽然还可以使用线段树、树状数组、splay等算法求解区间最值问题,但是ST算法比它们更快,更适用于在线查询。
ST算法分成两部分:离线预处理O(nlogn)和在线查询O(1)。
(1)离线预处理:运用DP思想求解区间最值,并将结果保存到一个二维数组中。
(2)在线查询:对给定区间进行分割,并借助上步中的二维数组求最值。
本题利用了ST算法求解RMQ问题,ST算法分预处理及询问两部分。要理解ST算法,首先要注意下文表述中的移位运算符 >>及<< 的优先级比四则运算 +-*/ 的优先级高。这样就能理解 1<<(j-1) 及 1<<j-1 代表不同的运算,即 1<<(j-1) 等价于 2^(j-1),1<<j-1 等价于 2^j-1。
(1)预处理
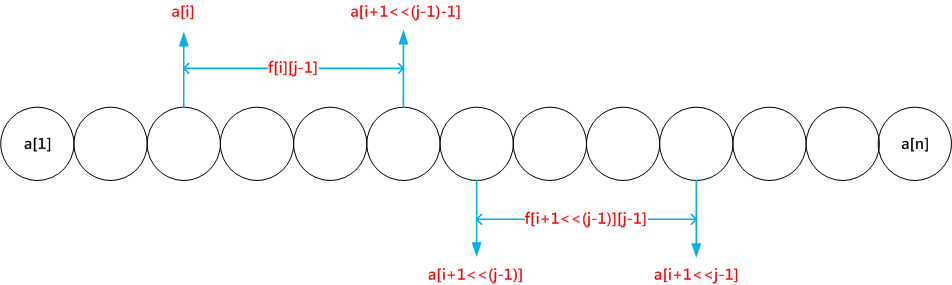
ST算法首先约定用 a[1] ~ a[n] 表示给定的一组数,f[i][j]表示从 a[i] ~ a[i+1<<j-1] 范围内的最大值,也即以 a[i] 为起点的连续 2^j 个数的最大值(∵ a[x] ~ a[y] 包含有 y-x+1 个数)。由于ST算法用到了倍增思想,因此自然有将 2^j 个数从中间平均分成两等分的实践,显然每一部分有 1<<(j-1) 个数,即2^(j-1) 个数。显然,初始范围 a[i] ~ a[i+1<<j-1] 被等分后,第一部分范围为 a[i] ~a[i+1<<(j-1)-1],第二部分范围为 a[i+1<<(j-1)] ~ a[i+1<<j-1],分别对应于 f[i][j-1] 和 f[i+1<<(j-1)][j-1]。
综上,得 f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1])。
(2)查询
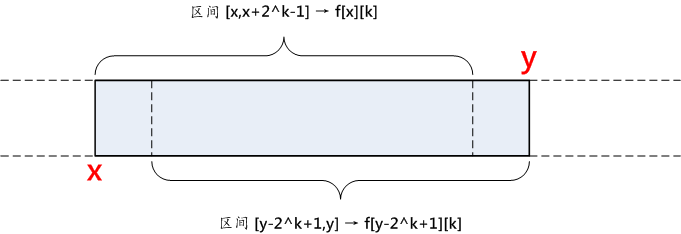
若给定查询区间 [x,y],若利用ST算法求此区间内的最大值。则需先求出最大的 k,使之满足 2^k ≤ y-x+1。
在此基础上,区间 [x,y]=[x,x+2^k-1]∪[y-2^k+1,y],则区间 [x,y] 内的最大值为 max(f[x][k],f[y-(1<<k)+1][k])。
据上,利用ST算法查询区间 [x,y] 的最大值,计算式如下:
k=log2(y-x+1)
max(f[x][k],f[y-(1<<k)+1][k])
● 快读:https://blog.csdn.net/hnjzsyjyj/article/details/120131534
int read() { //fast readint x=0,f=1;char c=getchar();while(c<'0' || c>'9') { //!isdigit(c)if(c=='-') f=-1;c=getchar();}while(c>='0' && c<='9') { //isdigit(c)x=x*10+c-'0';c=getchar();}return x*f;
}● 链式前向星:https://blog.csdn.net/hnjzsyjyj/article/details/139369904
val[idx]:存储编号为 idx 的边的值
e[idx]:存储编号为 idx 的结点的值
ne[idx]:存储编号为 idx 的结点指向的结点的编号
h[a]:存储头结点 a 指向的结点的编号
【算法代码】
#include<bits/stdc++.h>
using namespace std;const int maxn=5e5+5;
const int maxm=maxn<<1;
int f[maxn<<1][20]; //log2(5e5)<20;
int id[maxn<<1][20];
int h[maxn],e[maxm],ne[maxm],idx;
bool st[maxn];
int ola[maxn],a[maxn<<1],dep[maxn];
int n,m,root;
int tot;inline int read() { //fast readint x=0,f=1;char c=getchar();while(c<'0' || c>'9') { //!isdigit(c)if(c=='-') f=-1;c=getchar();}while(c>='0' && c<='9') { //isdigit(c)x=x*10+c-'0';c=getchar();}return x*f;
}inline void add(int a,int b) {e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}inline void ola_seq1(int u,int fa) {a[++tot]=u;ola[u]=tot;dep[u]=dep[fa]+1;st[u]=true;for(int i=h[u]; ~i; i=ne[i]) {int j=e[i];if(j==fa) continue;if(!st[j]) ola_seq1(j,u);a[++tot]=u;}
}int main() {memset(h,-1,sizeof(h));n=read(),m=read(),root=read();for(int i=1; i<n; i++) {int x=read(),y=read();add(x,y);add(y,x);}ola_seq1(root,0);for(int i=1; i<=tot; i++) {f[i][0]=dep[a[i]];id[i][0]=a[i];}for(int j=1; j<=20; j++)for(int i=1; i<=tot-(1<<j)+1; i++) {if(f[i][j-1]>f[i+(1<<(j-1))][j-1]) {f[i][j]=f[i+(1<<(j-1))][j-1];id[i][j]=id[i+(1<<(j-1))][j-1];} else {f[i][j]=f[i][j-1];id[i][j]=id[i][j-1];}}for(int i=1; i<=m; i++) {int le=read(),ri=read();le=ola[le],ri=ola[ri];if(ri<le) swap(le,ri);int k=log2(ri-le+1); //emphasis if(f[le][k]<f[ri-(1<<k)+1][k]) printf("%d\n",id[le][k]);else printf("%d\n",id[ri-(1<<k)+1][k]);}return 0;
}/*
in:
5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5out:
4
4
1
4
4
*/
【参考文献】
https://www.jianshu.com/p/050b589d039e
https://blog.csdn.net/dingqiongliang0363/article/details/102168530
https://www.cnblogs.com/lyttt/p/17355807.html
https://blog.csdn.net/weixin_44035017/article/details/99480717
https://blog.csdn.net/weixin_45963335/article/details/107912901
https://www.cnblogs.com/mpeter/articles/11324817.html
https://blog.csdn.net/diaoqi6581/article/details/101999564
https://blog.csdn.net/m0_37809890/article/details/82856158
这篇关于洛谷 P3379:最近公共祖先(LCA)← RMQ+欧拉序的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



