lca专题
poj1330(LCA最近公共祖先)
题意:求最近公共祖先 思路:之前学习了树链剖分,然后我就用树链剖分的一小部分知识就可以解这个题目了,记录每个结点的fa和depth。然后查找时,每次将depth大的结点往上走直到x = y。 代码如下: #include<iostream>#include<algorithm>#include<stdio.h>#include<math.h>#include<cstring>
【HDU】5574 Colorful Tree【子树染色,询问子树颜色数——线段树+bit+lca+set】
题目链接:【HDU】5574 Colorful Tree 题目大意:对一个子树染色,询问一个子树的颜色数。 题目分析: set set维护每种颜色所在的 dfs dfs序区间,修改均摊 nlogn nlogn。 #include <bits/stdc++.h>using namespace std ;typedef long long LL ;typedef pair < int , i
【LCA】vijos1427机密信息
描述 Lorabit有个很奇怪的习惯,他把他所有的机密信息都存放在一个叫机密盘的磁盘分区里,然而这个机密盘中却没有一个文件,那他是怎么存放信息呢?聪明的你一定想到了,Lorabit的信息都是以文件夹名称的形式保存的。Lorabit给机密盘中的每一个文件夹都编了号,而Lorabit的机密信息是由S文件夹转到T文件夹的过程中必须经过的文件夹名称组合而成的(包括S和T),由于Lorabit的磁盘很
【LCA】求最近公共祖先
算法一:在线算法 倍增 POJ1330 模板题 #include <stdio.h>#include <string.h>#include <iostream>#include <algorithm>#include <vector>#include <queue>#include <set>#include <map>#include <string>#include
poj 3694 Network(tarjan + LCA)
http://poj.org/problem?id=3694 题意:对于一个无向连通图,问加入某条边后,图中有桥的数目。 思路: 根据tarjan算法求出初始图的桥的数目,并用数组bridge标记桥的终点,在tarjan深搜树中求出每个节点的父节点(数组father表示)以及它们的深度,用于以后迭代求LCA。 因为加入某条边后,树中就会存在环,而环中的每条边都不再是桥,这就与求LCA
poj 1330 Nearest Common Ancestors(LCA模板)
http://poj.org/problem?id=1330 题意:给出两个点,求出这两个点最近的公共祖先。 求LCA的模板题。 大致思路就是访问到某个节点时,先将它自己加入集合中,然后递归访问它的子树,同时把子树加入到集合中来。子树搜索完毕后,判断该节点是否是输入的两个节点之一,若是,并且另外一个也已标记为访问过,那么另外一个节点的祖先便是他们的LCA。 #include<stdio
最近公共祖先(LCA),树上差分,树的直径总结
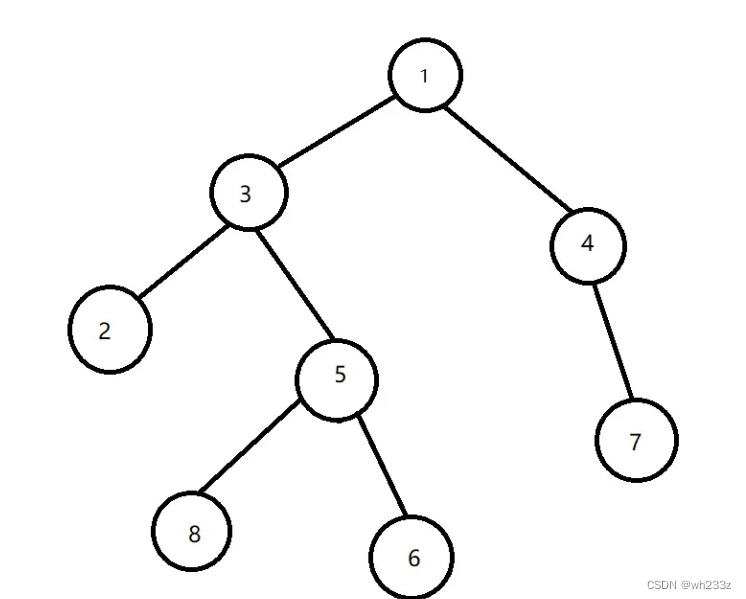
最近也是一不小心就学到了树论,这方面确实太不行了,也该开始学习一下了,那么话不多说,进入今日份的树论学习,直接开冲 最近公共祖先(LCA)——倍增思想(可以结合我之前写的ST表学习) 我们来看什么是最近公共祖先,对于9和8来讲,其最近公共祖先为6,对于3和7来讲,其最近公共祖先为5,那么我们去求最近公共祖先总共要有两步 第一步就是深搜,我们这一遍的深搜主要是为了去统计每一个点的深度
HDU 5150 UVALive 5061 (LCA标记)
这两题都是在树上求某一些路径上的点权的变化 两道题的思路相同 HDU 5150: 每一种颜色我们分开考虑他们对所有节点的贡献,对于颜色同为c的两个节点u和v(假设u!=v),那么在lca(u,v)的时候我们需要-1,因为在lca(u,v)一直到根的路径上,颜色c只能影响一次。基于此,我们对每种颜色的所有节点按照dfs序排好序,首先每个节点+1,然后对dfs序相邻的两个节点(注意颜色要相同)求
C++ P3379 【模板】最近公共祖先(LCA)
题目地址:https://www.luogu.org/problemnew/show/P3379 主要是用来作为参考代码的。 #include<cstdio>#include<iostream>using namespace std;int cnt=0,head[1000010],f[500010][21],d[1000010];struct Edge{int v,nxt;}e
hdu 2586 树上点对最近距离 (lca)
,只要知道dis[i][j]=dis[i][root]+dis[j][root]-2*dis[Lca(i,j)][root]. 其中root为树的根节点,LCA(i,j)为i,j的最近公共祖先。 所以我们先把所有的询问储存下来,然后离线直接查询。复杂度是o(n+q)的。 VIE #include<cstdio>#include<algorithm>#include<i
poj 1330 LCA 最近公共祖先
水题目。直接上代码了。 VIEW CODE #include<cstdio>#include<algorithm>#include<iostream>#include<cmath>#include<queue>#include<stack>#include<string>#include<cstring>#include<map>#include<vector>#
洛谷 P3379:最近公共祖先(LCA)← RMQ+欧拉序
【题目来源】https://www.luogu.com.cn/problem/P3379【题目描述】 如题,给定一棵有根多叉树,请求出指定两个点直接最近的公共祖先。【输入格式】 第一行包含三个正整数 N,M,S,分别表示树的结点个数、询问的个数和树根结点的序号。 接下来 N−1 行每行包含两个正整数 x,y,表示 x 结点和 y 结点之间有一条直接连接的边(数据保证可以构成树)。 接下来 M 行每
hdu5156 LCA
具体解法就是bc首页的解法了,排个颜色序和dfs序,然后按照解法一路解下去就行了。注意一定要pai排dfs序,不然会更新错误的公共祖先节点。 代码: #include <iostream>#include <cstring>#include <cstdio>#include <queue>#include <stack>#include <map>#include <strin
PKU Campus 2011 B A Problem about Tree lca倍增
B:A Problem about Tree 总时间限制: 1000ms 内存限制: 65536kB 描述 Given a tree with Nvertices and N- 1 edges, you are to answer Qqueries on "which vertex isY's parent if we choose Xas the ro
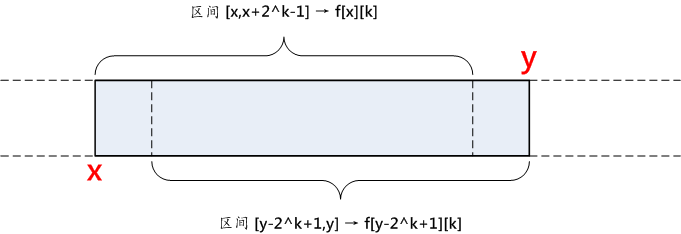
hdu 5266 pog loves szh III LCA+RMQ
题意: 给你一棵树,然后询问l~r节点的最近公共祖先(LCA)。 思路: 用RMQ维护一段区间的LCA,然后询问时,将两个区间的LCA再求一次LCA即可。 code: #pragma comment(linker, "/STACK:102400000,102400000")#include <cstdlib>#include <cstdio>#include <cstring>
hdu 5449 Robot Dog(期望+lca)
hdu 5449 Robot Dog(期望+lca) 题目链接:hdu 5449 Robot Dog 解题思路 n有50000,询问次数有100,每次询问的路径点数最多有100,对于不同询问去做动态规划,开一个 dp[u][i] dp[u][i]表示在第u个节点匹配了i个的期望,显然最坏情况下dp数组的每个状态都要遍历到,复杂度为 o(nqp) o(nqp),不能接受。 换个想法,如果我们
蓝桥杯2023(十四届)省赛——景区导游(最近公共祖先LCA)
景区导游(最近公共祖先) 1.景区导游 - 蓝桥云课 (lanqiao.cn) 本来一开始想用Floyd算法,看看能不能水个分的,但是实际上,居然运行错误呜呜呜呜。 但是实际上和我一开始分析的是一样的,最近公共祖先。但是我看题解上可以使用dfs暴力搜出来,我想试试。 来总结一下这道题的核心:树中两个节点之间的距离=二者到最近公共祖先的距离之和,所以,我们需要知道最近公共祖先是哪个。这里还有
hdu4912 Paths on the tree --- LCA贪心
给一棵n个结点的树,m条路径的起点和终点, 问至多可以选择多少条路径使其两两间没有公共点。 这题的主要问题是, 1、如何判断两条路径上没有交点 2、按什么策略来选 看上去感觉是最大匹配问题,但nm的范围较大问题1无法高效的解决。 画个图发现可能和LCA有关,但比赛时不知道这到底有什么用,完全没想贪心。 要选择尽量多,就是要尽量避免冲突。 我们选择一个点作为根,把给的边画出来建
何为LCA(最近共同祖先)?
原篇:(ACM算法)tarjan算法求LCA - 知乎 (zhihu.com) 顾名思义,就是求两个节点最近的共同祖先,就好比下图,2和3的共同祖先为3,2和4的共同祖先为1。 关于LCA求解有3种算法。 1.标记回溯法(也称暴力枚举,从一个点开始向上标记他的父节点,直接标记到根节点为止,然后另另一个点也开始向上回溯,当这个点被标记过,则找到这两个点的共同祖先),当数据过大时,很明显这个
【R语言篇】潜在类别分析(Latent Class Analysis, LCA)及其在R语言中的实现
1. 潜在类别分析简介 潜在类别分析(LCA)是一种用于识别样本中潜在子群的统计方法。这种方法基于观察到的数据来估计个体属于不同潜在类别的概率。LCA广泛应用于社会科学、市场研究、生物医学等领域,尤其适用于处理分类数据。 2. LCA的核心思想 LCA的核心在于假设数据中存在若干未观测到的、互斥的类别,每个类别代表了一种特定的群体特征。通过分析,我们可以估计出每个个体属于各个潜在类别的概率,进而
洛谷 P3379 [模板] 最近公共祖先(LCA)
【模板】最近公共祖先(LCA) 题目描述 如题,给定一棵有根多叉树,请求出指定两个点直接最近的公共祖先。 输入格式 第一行包含三个正整数 N , M , S N,M,S N,M,S,分别表示树的结点个数、询问的个数和树根结点的序号。 接下来 N − 1 N-1 N−1 行每行包含两个正整数 x , y x, y x,y,表示 x x x 结点和 y y y 结点之间有一条直接连
倍增法求lca(最近公共祖先)
思路: 大致上算法的思路是这样发展来的。 想到求两个结点的最小公共祖先,我们可以先把两个的深度提到同一水平,在一步一步往上跳,直到两个结点有了一个公共祖先,依照算法流程,这就是least common ancestor。 但是如果这样一步步地往上未免太让人着急,为了提高一下效率,便不再每次只跳一步,而跳2i 步。一般的,先这样蹦蹦跳跳跳上去直到两个结点相平,在两个一起这样蹦上去。 怎么确
最近公共祖先(LCA)的三种求解方法
转载来自:https://blog.andrewei.info/2015/10/08/e6-9c-80-e8-bf-91-e5-85-ac-e5-85-b1-e7-a5-96-e5-85-88lca-e7-9a-84-e4-b8-89-e7-a7-8d-e6-b1-82-e8-a7-a3-e6-96-b9-e6-b3-95/ 简述 LCA(Least Common Ancesto
最近公共祖先LCA问题(转)
本文转载from:july 问题描述 求有根树的任意两个节点的最近公共祖先。 分析与解法 解答这个问题之前,咱们得先搞清楚到底什么是最近公共祖先。最近公共祖先简称LCA(Lowest Common Ancestor),所谓LCA,是当给定一个有根树T时,对于任意两个结点u、v,找到一个离根最远的结点x,使得x同时是u和v的祖先,x 便是u、v的最近公共祖先。(参见:http://en.wi
Codeforces Contest 1062 problem E Company —— lca+主席树+dfs序
The company X has n employees numbered from 1 through n. Each employee u has a direct boss pu (1≤pu≤n), except for the employee 1 who has no boss. It is guaranteed, that values pi form a tree. Employe