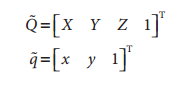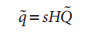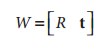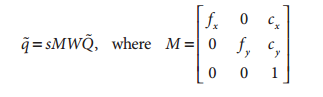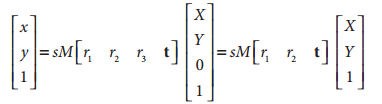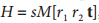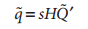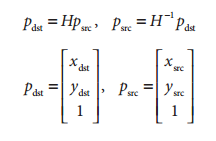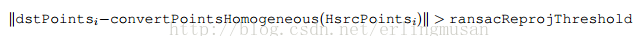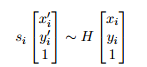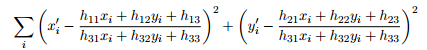本文主要是介绍Homography单应矩阵,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在计算机视觉中,平面的单应性被定义为一个平面到另外一个平面的投影映射。因此一个二维平面上的点映射到摄像机成像仪上的映射就是平面单应性的例子。如果点Q到成像仪上的点q的映射使用齐次坐标,这种映射可以用矩阵相乘的方式表示。若有一下定义:
则可以将单应性简单的表示为:
这里引入参数s,它是任意尺度的比例(目的是使得单应性定义到该尺度比例)。通常根据习惯放在H的外面。
H有两部分组成:用于定位观察的物体平面的物理变换和使用摄像机内参数矩阵的投影。
物理变换部分是与观测到的图像平面相关的部分旋转R和部分平移t的影响之和,表示如下
这里R为3*3大小的矩阵,t表示一个一个3维的列矢量。
摄像机内参数矩阵用M表示,那么我们重写单应性如下:
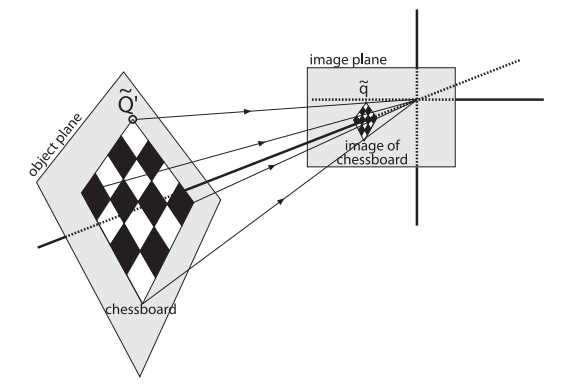
我们知道单应性研究的是一个平面上到另外一个平面的映射,那么上述公式中的~Q,就可以简化为平面坐标中的~Q',即我们使Z=0。即物体平面上的点我们用x,y表示,相机平面上的点,我们也是用二维点表示。我们去掉了Z方向的坐标,那么相对于旋转矩阵R,R可以分解为R=[r1 r2 r3],那么r3也就不要了,参考下面的推导:
其中H为:
是一个3×3大小的矩阵.
故最终的单应性矩阵可表示如下:
OpenCV就是利用上述公式来计算单应性矩阵。它使用同一物体的多个图像来计算每个视场的旋转和平移,同时也计算摄像机的内参数。我们知道旋转和平移共6个参数,摄像机内参数为4个参数。对于每一个视场有6个要求解的新参数和4个不变的相机内参数。对于平面物体如棋盘,能够提供8个方差,即映射一个正方形到四边形可以用4个(x,y)来描述。那么对于两个视场,我们就有8*2=16=2*6+4,即求解所有的参数,至少需要两个视场。
为什么正方形到四边形的四个点的映射可以确定8个方程呢,结果是显然的,我们假设物体平面上的正方形的一个顶点坐标为(u,v),成像仪与该点对应的点坐标为(x,y),我们假设它们之间的关系如下:
u=f(x,y);
v=g(x,y);
显然,我们把四点的对应坐标带入到上述公式可以得到8个方程。
这里我们会想物体平面上正方形的四个顶点坐标如何确定,其实我们就可以理解为角点的个数,对于尺度的话,我们有s进行控制。对于图像平面上的角点的位置,我们可以可以通过寻找角点来定位他们的位置。其实对于具体的操作,由于还没细读代码和相关原理,在这里只能大体猜测一下。等日后学习了,再来纠正。
单应性矩阵H把源图像平面上的点集位置与目标图像平面上(通常是成像仪平面)的点集位置联系起来:
opencv就是利用多个视场计算多个单应性矩阵的方法来求解摄像机内参数。
OpenCV提供了一个方便的C函数cvFindHomography(),函数接口如下:
1、src_points,dst_points为N×2或者N×3的矩阵,N×2表示点是以像素坐标表示。N×3表示以齐次坐标表示。
2、homography,为3*3大小的矩阵,用来存储输出的结果。
C++函数的接口:
1、srcPoints,dstPoints为CV_32FC2或者vector<Point2f>类型
2、method:0表示使用所有点的常规方法;CV_RANSAC 基于RANSAC鲁棒性的方法;CV_LMEDS 最小中值鲁棒性方法
3、ransacReprojThreshod 仅在RANSAC方法中使用,一个点对被认为是内层围值(非异常值)所允许的最大投影误差。即如果:
那么点i被认为是异常值。如果srcPoints和dstPoints单位是像素,通常意味着在某些情况下这个参数的范围在1到10之间。
4、status,可选的输出掩码,用在CV_RANSAC或者CV_LMEDS方法中。注意输入掩码将被忽略。
这个函数找到并且返回源图像平面和目的图像平面之间的透视变换矩阵H:
使得下面的返回投影误差(back-projection)最小:
如果参数method设置为默认值0,该函数使用一个简单的最小二乘方案来计算初始的单应性估计。
然而,如果不是所有的点对(srcPoints,dstPoints)都适应这个严格的透视变换。(也就是说,有一些异常值),这个初始估计值将很差。在这种情况下,我们可以使用两个鲁棒性算法中的一个。RANSCA和LMEDS这两个方法都尝试不同的随机的相对应点对的子集,每四对点集一组,使用这个子集和一个简单的最小二乘算法来估计单应性矩阵,然后计算得到单应性矩阵的质量quality/goodness。(对于RANSAC方法是内层围点的数量,对于LMeDs是中间的重投影误差)。然后最好的子集用来产生单应性矩阵的初始化估计和inliers/outliers的掩码。
忽略方法,鲁棒性与否,计算得到的单应性矩阵使用Levenberg-Marquardt方法来进一步减少重投影误差,从而进一步提纯。(对于鲁棒性的方法仅使用内围层点(inliers))。
RANSAC方法,几乎可以处理任含有何异常值比率的情况,但是它需要一个阈值用来区分inliers和outliers。LMeDS方法不需要任何阈值,但是它仅在inliers大于50%的情况下才能正确的工作。最后,如果你确信在你计算得到的特征点仅含一些小的噪声,但是没有异常值,默认的方法可能是最好的选择。(因此,在计算相机参数时,我们或许仅使用默认的方法)
这个函数用来找到初始化内参数和外参数矩阵。单应性矩阵取决于一个尺度,那么通常归一化,以使得h33=1。
[1] http://blog.csdn.net/yjl9122/article/details/50972320
[2] http://www.360doc.com/content/14/0410/14/10724725_367760906.shtml
[3] http://blog.csdn.net/jay463261929/article/details/53611363
[4] http://blog.csdn.net/sunshine_in_moon/article/details/45461819
[5] http://www.cnblogs.com/ml-cv/p/5871052.html
[6] http://blog.csdn.net/zinnc/article/details/52319491
[7] affine transformation: http://www.matongxue.com/madocs/244.html#/madoc
这篇关于Homography单应矩阵的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!