第三章线性判别 -二维向量投影

本文主要是介绍第三章线性判别 -二维向量投影，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

计算二维平面上的点到某向量w上的投影点。

import numpy as np
import matplotlib.pyplot as plt
x1=np.random.normal(7,1,[20,1])
x2=np.random.normal(7,1,[20,1])
C0=np.concatenate((x1,x2),axis=1).T #C0类x1=np.random.normal(2,1,[20,1])
x2=np.random.normal(2,1,[20,1])
C1=np.concatenate((x1,x2),axis=1).T #C1类w=np.array([[2.],[1.]])
w=w/np.sqrt(np.dot(w.T,w))#这里很重要，w一定是要转换成单位向量
print("w",w)#对C0类进行投影
P0=(np.dot(w.T,C0))#该投影点是w单位向量的距离
M0=w*(P0)#转换成坐标点#对C1类进行投影
P1=(np.dot(w.T,C1))#该投影点是w单位向量的距离
M1=w*(P1)#转换成坐标点#C0的向量均值计算投影点
u0=np.mean(C0,axis=1)
print('u0',u0)
C0_mean_len=np.dot(w.T,u0)#均值点在w向量上的长度
C0_avg_point=w*C0_mean_len#计算点坐标
print("M0_avg_point",C0_avg_point)
#C1的向量均值计算投影点
u1=np.mean(C1,axis=1)
print('C1_avg',u1)
C1_mean_len=np.dot(w.T,u1)#均值点在w向量上的长度
C1_avg_point=w*C1_mean_len#计算点坐标
print("M1_avg_point",C1_avg_point)#对两类点进行描点
plt.scatter(C0[0],C0[1])
plt.scatter(C1[0],C1[1])#画出w向量的直线
plt.plot([0,w[0][0]*15],[0,w[1][0]*15])#画出两类点的投影点
plt.scatter(M0[0],M0[1])
plt.scatter(M1[0],M1[1])#画出两类均值点的投影点
plt.scatter(C0_avg_point[0],C0_avg_point[1],marker="*",c='r',s=100)
plt.scatter(C1_avg_point[0],C1_avg_point[1],marker="*",c='k',s=100)ax = plt.gca()
ax.set_aspect(1)
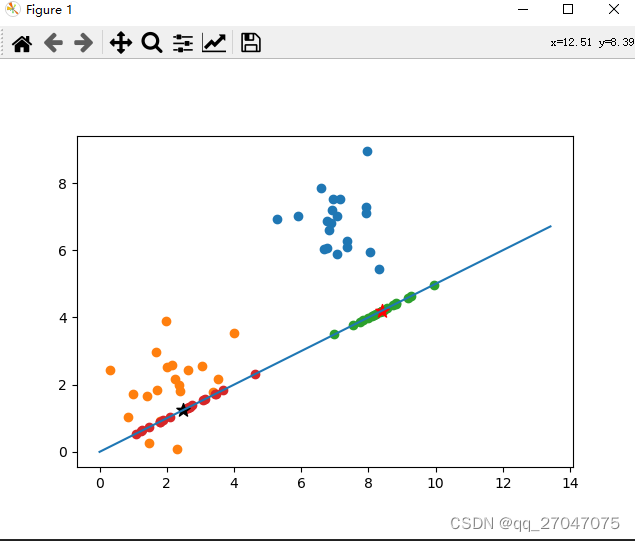
plt.show()

结果如图：五角星点为均值投影点。