本文主要是介绍【优选算法】分治 {三分快排:三指针优化,随机选key,快速选择算法;归并排序:统计数组中的逆序对,统计数组中的翻转对;相关编程题解析},希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、经验总结
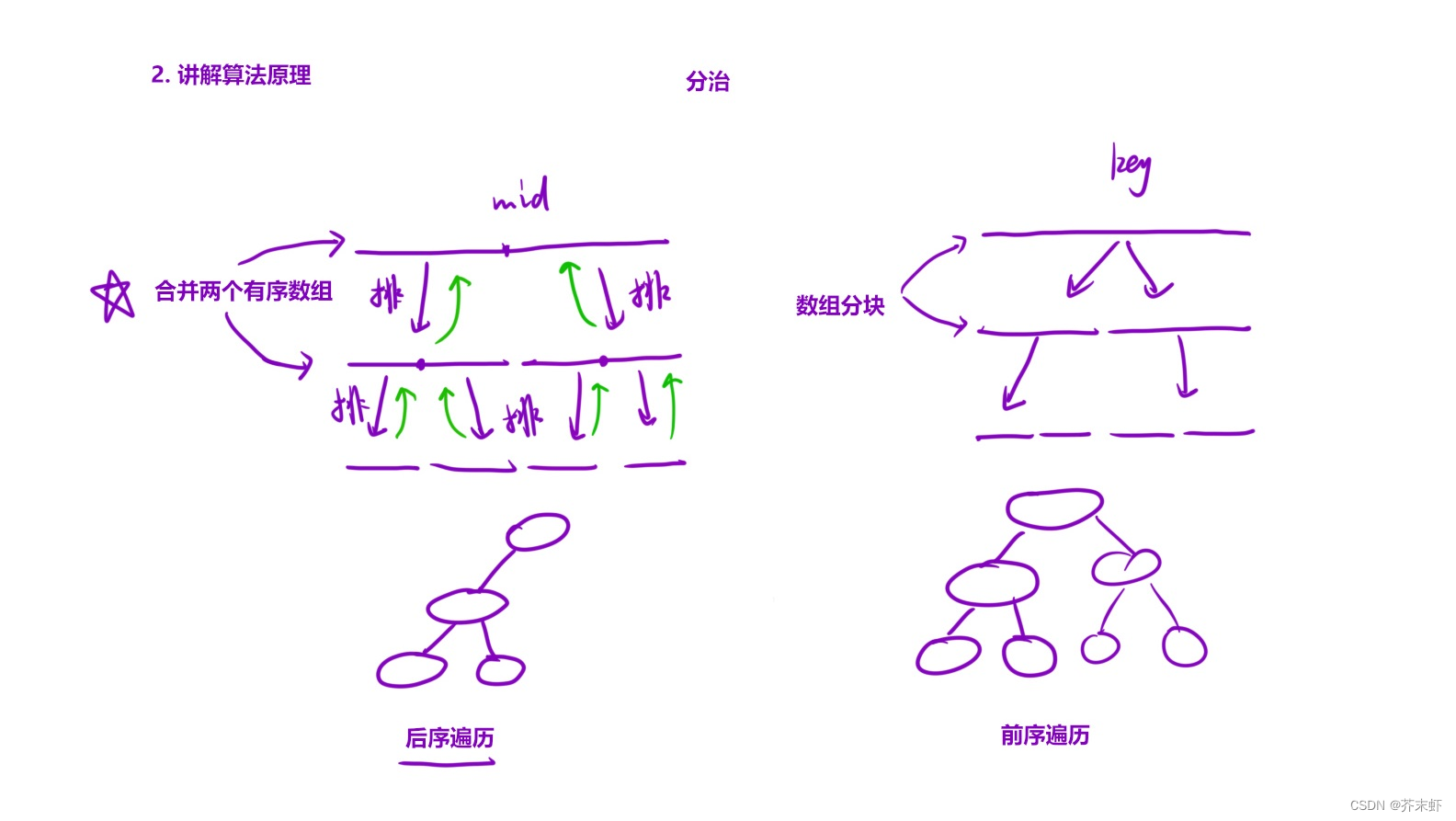
1.1 三分快排
优化一:三指针优化
之前学习的快速排序无法妥善处理相等或重复序列的排序问题(有序且三数取中无效),使快速排序的效率无法达到最优。
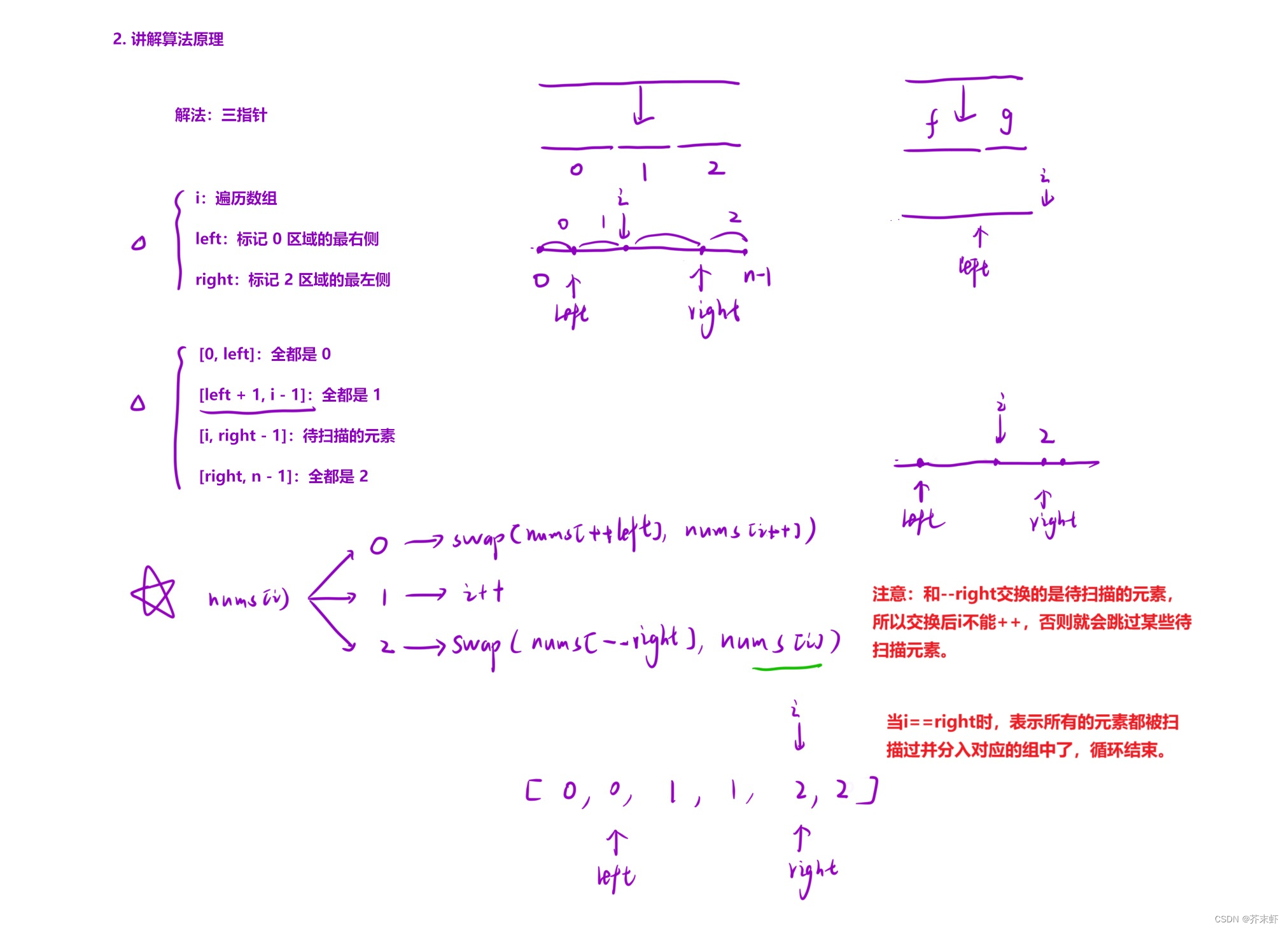
为了解决重复序列的问题,我们将原先的双指针法(前后指针)优化为三指针,将数组划分成三块:
- [0, left]:< key
- [left+1, right-1]:==key
- [riight, n-1]:> key
- 其中left标记<key区间的最右侧;i负责从左向右遍历数组;right标记>key区间的最左侧;
之后,再利用分治思想将<key和>key的部分进行排序即可,所有==key的部分已经移动到了最终的位置上。完美的解决了重复序列的问题。
举个极端一点的例子,对于全体重复的序列,原先需要partition n次,每次都要将区间遍历一遍是一个典型的复杂度为O(N^2)的算法。现在,仅需要partition一次就可以将所有数字归入==key的区间,不再有<key和>key的部分排序结束,复杂度降为O(N)。
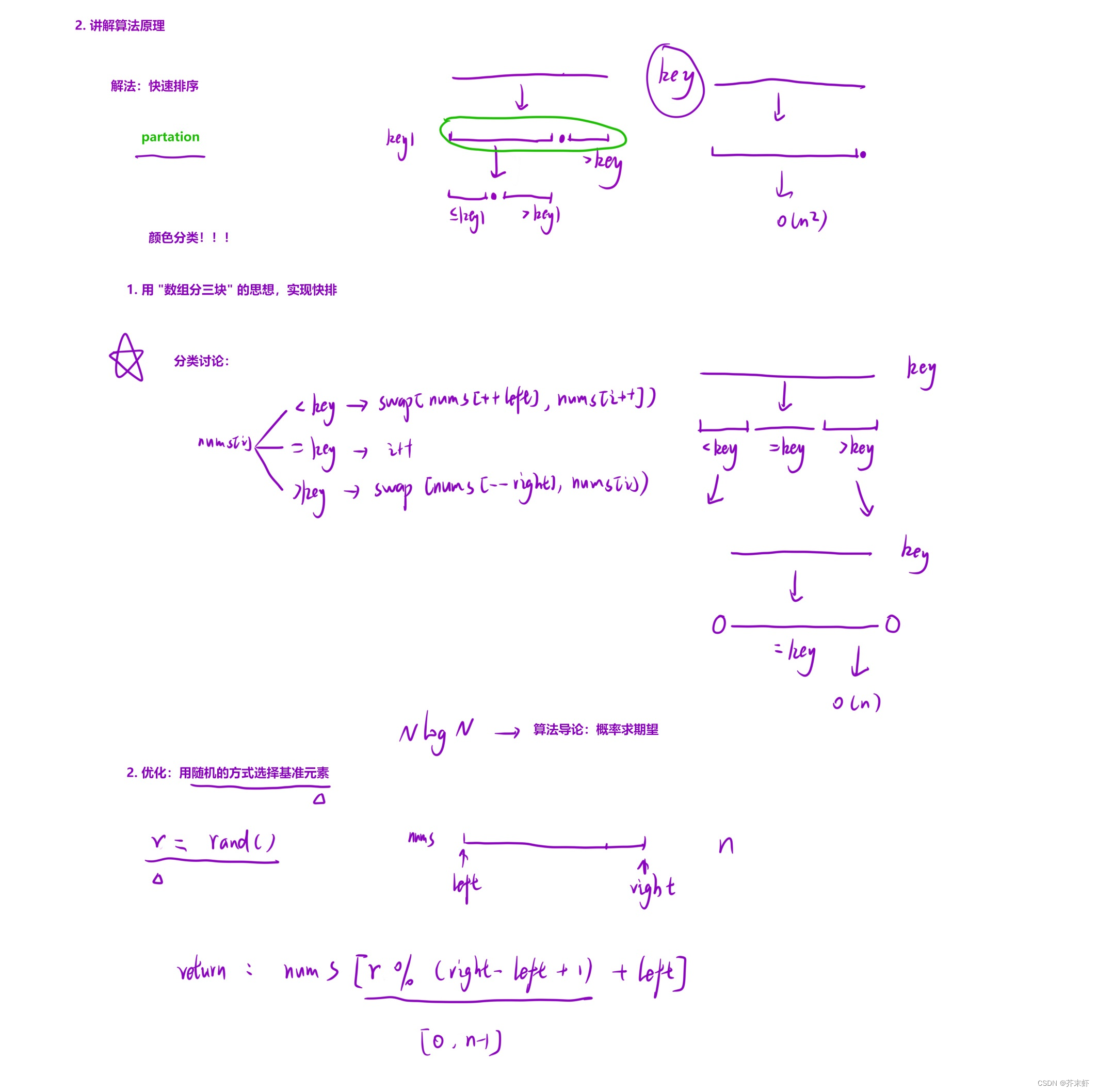
优化二:随机选key
之前我们使用的是取最左(右)值为key、三数取中为key。实际上随机取key可以使数组划分的更为均匀,每个区间都是等概率划分的。使快速排序的时间复杂度更接近于O(NlogN)。
三分快排的应用:快速选择算法
快速选择算法是解决Topk问题的最优方案,之前学习过的利用堆解决Topk问题时间复杂度为O(NlogK),已经相当高效了。但是快速选择算法可以将时间复杂度优化为O(N)。
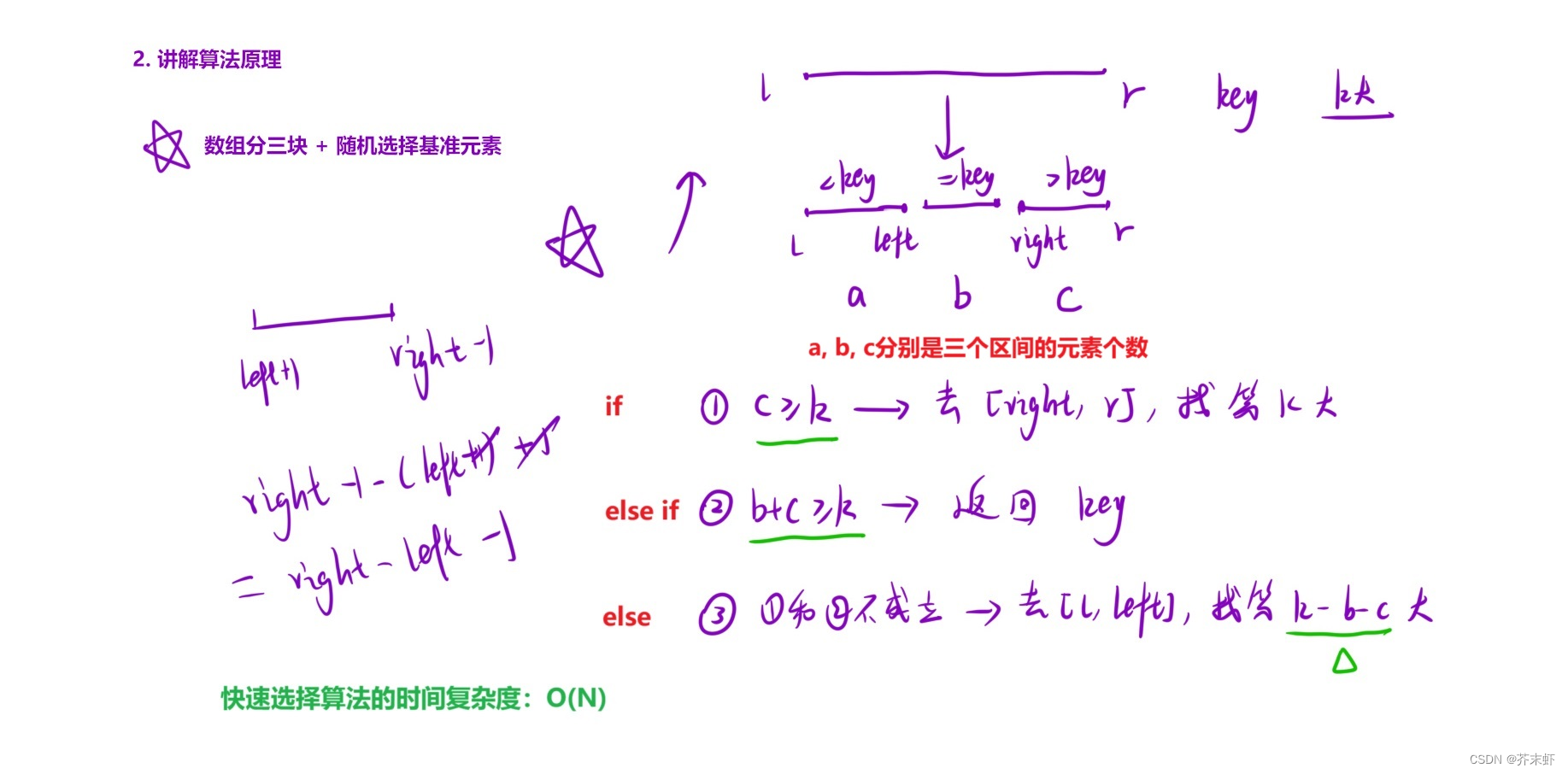
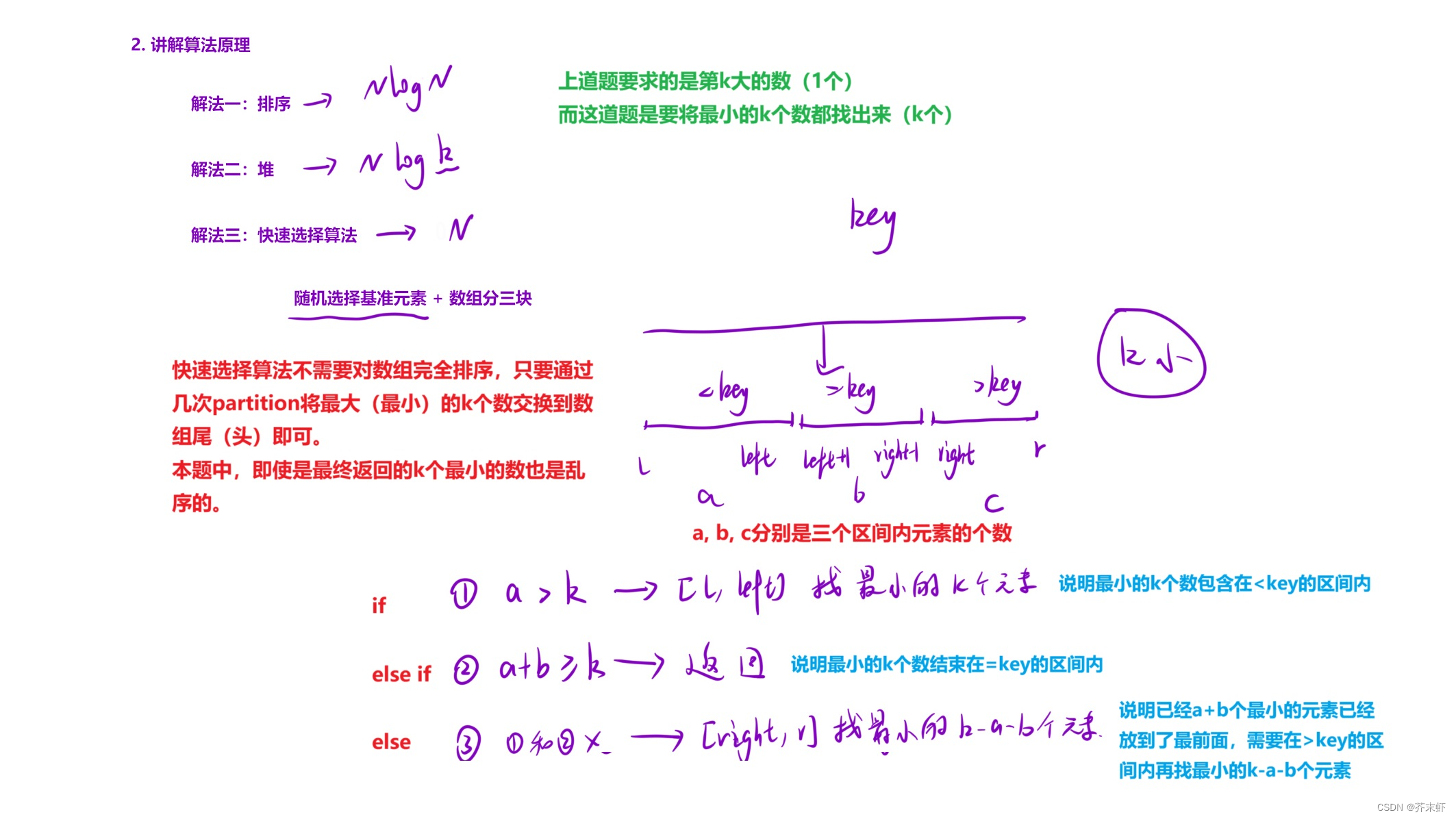
快速选择算法的原理是基于三分快排的,但并不需要将数组完全排序,而是将数组划分为三块以后,将三块区间内元素的个数与k比较,再进行递归分割,直到将最小(最大)的前k个数全部移动到数组前面(后面)。
Topk问题又分前k小(大)、第k小(大)。前k小只需要将最小的前k个数全部移动到数组前面即可,<key区间内的元素个数只要==k就可以返回。而第k小不仅要移动最小的前k个数,还必须找到第k个,即第k个数必须刚好落在==key的区间内才能返回。
1.2 归并排序
利用归并排序统计数组中的逆序对
所谓逆序对是指前大后小的一对数,利用归并排序统计逆序对可以将暴力解法的时间复杂度O(N^2),优化为O(NlogN)。算法思路如下:
- 将数组从中间一分为二,先统计左右区间内的逆序对,并进行排序。
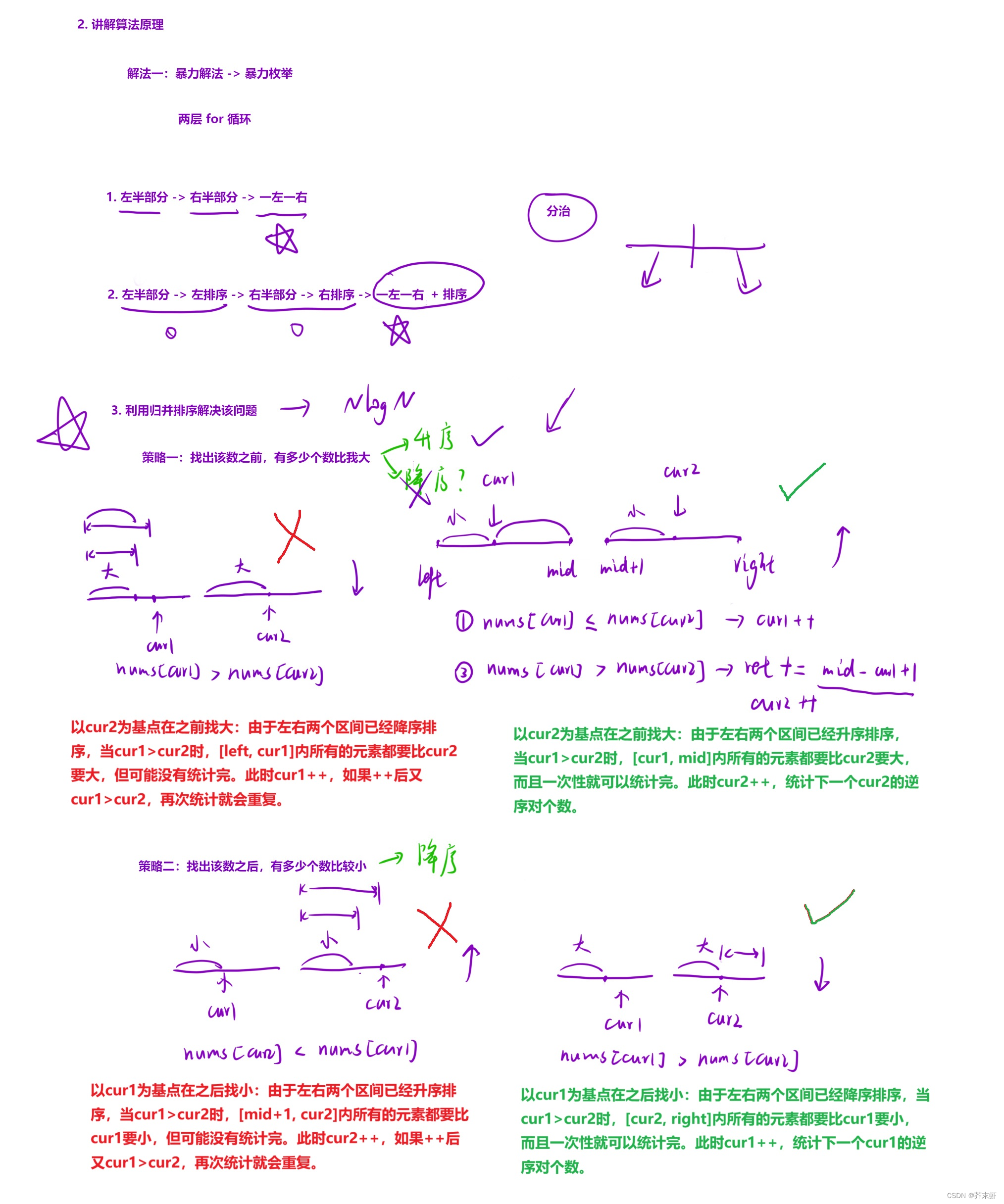
- 然后再归并左右区间的过程中,统计一左一右跨两个区间的逆序对,有两个策略可供选择
- 升序排序:以右区间中的元素cur2为基点,在左区间中找大于cur2的元素cur1,因为是升序所以左区间之后的元素都大。
- 降序排序:以左区间中的元素cur1为基点,在右区间中找小于cur1的元素cur2,因为是降序所以右区间之后的元素都小
- 颠来倒去其实都是在cur1 > cur2的时候,统计逆序对的数量,只是基点不同:先左后右是降序,先右后左是升序
- 逆序对的判定规则与左右区间归并的比较规则相同,所以可以在左右区间归并的过程中顺道统计逆序对的个数。
利用归并排序统计数组中的翻转对
不同于逆序对,翻转对要求前一个数大于后一个数的两倍。翻转对的判定规则与左右区间归并的比较规则不同,也就不能顺道了。但是翻转对的判定与统计仍然可以利用归并排序的分治和左右区间有序的条件,只是需要在左右区间归并之前,先一步进行一左一右的翻转对统计即可。
在统计一左一右跨两个区间的翻转对时,算法规律和逆序对相同:在cur1/2 > cur2(乘法改除法防溢出)的时候,统计翻转对的数量。先左后右是降序,先右后左是升序。算法还可以使用同向双指针进行优化,只需要将左右两个区间遍历一遍O(N),就可以完成统计。不会影响整体归并排序的复杂度O(NlogN)。
二、相关编程题
2.1 三分快排
2.1.1 颜色分类
题目链接
75. 颜色分类 - 力扣(LeetCode)
题目描述

算法原理
编写代码
class Solution {
public:void sortColors(vector<int>& nums) {int n = nums.size();int left = -1, i = 0, right = n;while (i < right) {if (nums[i] == 0) {if (++left != i)swap(nums[left], nums[i]);++i;} else if (nums[i] == 1) {++i;} else if (nums[i] == 2 && --right != i) {swap(nums[i], nums[right]);}}}
};
2.1.2 优化快速排序
题目链接
912. 排序数组 - 力扣(LeetCode)
题目描述

算法原理
编写代码
class Solution {
public:vector<int> sortArray(vector<int>& nums) {srand(time(nullptr));QuickSort(nums, 0, nums.size()); //注意区间是左闭右开return nums;}void QuickSort(vector<int>& nums, int begin, int end){if(end - begin < 2) return;int key = nums[rand()%(end-begin)+begin]; //随机取keyint left = begin-1, i = begin, right = end;while(i < right){if(nums[i] < key) swap(nums[++left], nums[i++]);else if(nums[i] == key) ++i;else swap(nums[--right], nums[i]);}//left和right都是闭端点QuickSort(nums, begin, left+1); //left做end需要+1(右开)QuickSort(nums, right, end); //right做begin不需要+1(左闭)}
};
2.1.3 数组中的第k个最大元素
题目链接
215. 数组中的第K个最大元素 - 力扣(LeetCode)
题目描述

算法原理
编写代码
//快速选择算法 O(N)
class Solution {
public:int findKthLargest(vector<int>& nums, int k) {srand(time(nullptr));return QuickSelect(nums, 0, nums.size()-1, k); //注意区间是左闭右闭}int QuickSelect(vector<int>& nums, int begin, int end, int k){// 当区间内只有一个元素时,直接返回这个元素if(begin == end) return nums[begin];// 随机选keyint key = nums[rand()%(end-begin+1)+begin]; // 将区间内的元素划分成三块int left = begin-1, i = begin, right = end+1;while(i < right){if(nums[i] < key) swap(nums[++left], nums[i++]);else if(nums[i] == key) ++i;else swap(nums[--right], nums[i]);}//核心逻辑if(end-right+1 >= k) //c>=kreturn QuickSelect(nums, right, end, k); else if(end-left >= k) //b+c>=kreturn key;else return QuickSelect(nums, begin, left, k-(end-left)); //找k-b-c大的数}
};//堆算法 O(NlogK)
class Solution {
public:Kint findKthLargest(vector<int>& nums, int k) {vector<int> leastHeap(k);for(int i = 0; i < k; ++i){leastHeap[i] = nums[i];}for(int i = k-2/2; i >= 0; --i){AdjustDown(leastHeap, i);}for(int i = k; i < nums.size(); ++i){if(nums[i] > leastHeap[0]) {leastHeap[0] = nums[i];AdjustDown(leastHeap, 0);}}return leastHeap[0];}void AdjustDown(vector<int>& nums, int root) {int parent = root;int child = parent * 2 + 1;int n = nums.size();while (child < n) {if (child + 1 < n && nums[child + 1] < nums[child]) {++child;}if (nums[child] < nums[parent]) {swap(nums[child], nums[parent]);parent = child;child = parent * 2 + 1;} else {break;}}}
};
2.1.4 最小的k个数
题目链接
LCR 159. 库存管理 III - 力扣(LeetCode)
题目描述

算法原理
编写代码
class Solution {
public:vector<int> inventoryManagement(vector<int>& stock, int cnt) {srand(time(nullptr));if(cnt > 0)QuickSelect(stock, 0, stock.size()-1, cnt);return vector<int> (stock.begin(), stock.begin()+cnt);}void QuickSelect(vector<int>& nums, int begin, int end, int k){// 当区间内只有一个元素时,直接返回if(begin == end) return;// 随机选keyint key = nums[rand()%(end-begin+1)+begin]; // 将区间内的元素划分成三块int left = begin-1, i = begin, right = end+1;while(i < right){if(nums[i] < key) swap(nums[++left], nums[i++]);else if(nums[i] == key) ++i;else swap(nums[--right], nums[i]);}//核心逻辑if(left-begin+1 > k) //a>kQuickSelect(nums, begin, left, k); else if(right-begin >= k) //a+b>=kreturn;else QuickSelect(nums, right, end, k-(right-begin)); }
};
2.2 归并排序
2.2.1 归并排序
题目链接
912. 排序数组 - 力扣(LeetCode)
题目描述

算法原理
编写代码
class Solution {
public:vector<int> sortArray(vector<int>& nums) {vector<int> tmp(nums.size()); //辅助数组在递归外创建效率更高MergeSort(nums, 0, nums.size(), tmp);return nums;}void MergeSort(vector<int>& nums, int begin, int end, vector<int>& tmp){if(end-begin < 2) return;int begin1 = begin;int end1 = begin+(end-begin)/2;int begin2 = end1;int end2 = end;MergeSort(nums, begin1, end1, tmp);MergeSort(nums, begin2, end2, tmp);//归并左右两顺序区间int i = begin;while(begin1 < end1 && begin2 < end2){if(nums[begin1] <= nums[begin2]){tmp[i++] = nums[begin1++];}else{tmp[i++] = nums[begin2++];}}while(begin1 < end1){tmp[i++] = nums[begin1++];}while(begin2 < end2){tmp[i++] = nums[begin2++];}for(int i = begin; i < end; ++i){nums[i] = tmp[i];}}
};
2.2.2 数组中的逆序对
题目链接
LCR 170. 交易逆序对的总数 - 力扣(LeetCode)
题目描述

算法原理
编写代码
class Solution {
public:int reversePairs(vector<int>& record) {vector<int> tmp(record.size());return MergeSort(record, 0, record.size(), tmp);}int MergeSort(vector<int>& nums, int begin, int end, vector<int>& tmp){//如果区间内的元素个数小于2,返回0个逆序对if(end-begin < 2) return 0;//将区间从中间划分成左右两个区间int begin1 = begin;int end1 = begin+(end-begin)/2;int begin2 = end1;int end2 = end;int cnt = 0;//左区间的个数+排序;右区间的个数+排序cnt += MergeSort(nums, begin1, end1, tmp);cnt += MergeSort(nums, begin2, end2, tmp);//一左一右的个数+归并排序//策略一:以cur2为基点,在之前找大int i = begin;while(begin1 < end1 && begin2 < end2){if(nums[begin1] <= nums[begin2]){tmp[i++] = nums[begin1++];}else{cnt += end1-begin1;tmp[i++] = nums[begin2++];}}//策略二:以cur1为基点在之后找小// while(begin1 < end1 && begin2 < end2)// {// if(nums[begin1] > nums[begin2])// {// cnt += end2 - begin2;// tmp[i++] = nums[begin1++];// }// else// {// tmp[i++] = nums[begin2++];// }// }while(begin1 < end1){tmp[i++] = nums[begin1++];}while(begin2 < end2){tmp[i++] = nums[begin2++];}//将归并排序好的区间元素拷贝回原数组for(int i = begin; i < end; ++i){nums[i] = tmp[i];}return cnt; //返回的就是区间内的逆序对总数}
};
2.2.3 计算右侧小于当前元素的个数
题目链接
315. 计算右侧小于当前元素的个数 - 力扣(LeetCode)
题目描述

算法原理
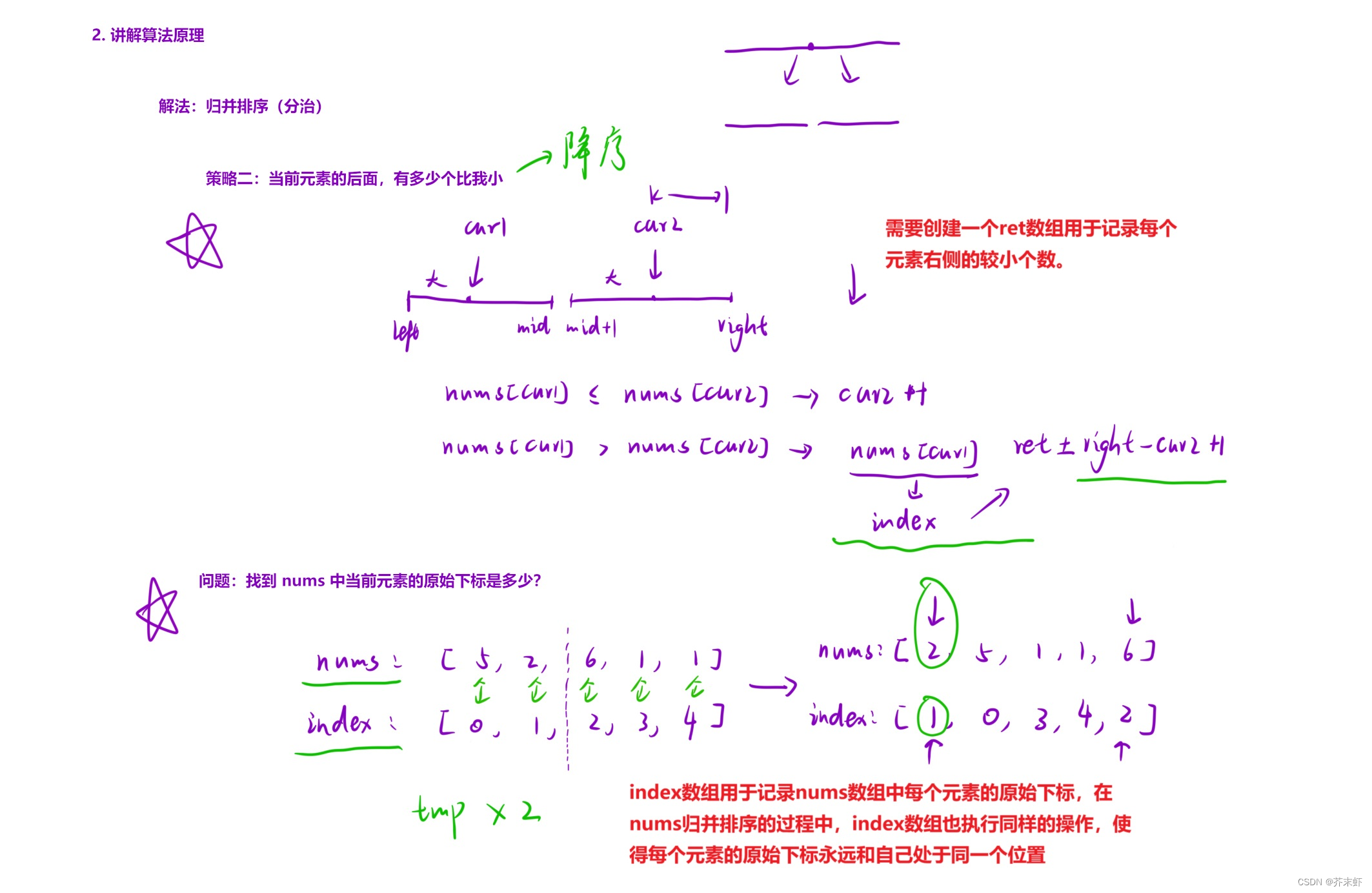
编写代码
class Solution {vector<int> tmp1, tmp2;
public:vector<int> countSmaller(vector<int>& nums) {tmp1.resize(nums.size()); //用于归并排序numstmp2.resize(nums.size()); //用于归并index,并不是排序,只是执行和nums同样的操作vector<int> ret(nums.size(), 0); //结果数组vector<int> index(nums.size()); //用于映射每个元素的原始下标for(int i = 0; i < nums.size(); ++i){index[i] = i;}MergeSort(nums, 0, nums.size(), ret, index);return ret;}void MergeSort(vector<int>& nums, int begin, int end, vector<int>& ret, vector<int>& index){if(end - begin < 2) return;//将数组从中间分成两个区间int begin1 = begin;int end1 = begin1+(end-begin)/2;int begin2 = end1;int end2 = end;//先分别处理左右区间内的个数MergeSort(nums, begin1, end1, ret, index);MergeSort(nums, begin2, end2, ret, index);//再处理一左一右的个数int i = begin;while(begin1 < end1 && begin2 < end2){if(nums[begin1] > nums[begin2]) //降序排序{ret[index[begin1]] += end2-begin2; //注意:1.获取元素的原始下标 2.+=可能在左右区间中已经统计过了tmp1[i] = nums[begin1];tmp2[i++] = index[begin1++]; //nums数组中的元素移动到哪,index数组中的原始下标就移动到哪}else{tmp1[i] = nums[begin2];tmp2[i++] = index[begin2++];}}while(begin1 < end1){tmp1[i] = nums[begin1];tmp2[i++] = index[begin1++];}while(begin2 < end2){tmp1[i] = nums[begin2];tmp2[i++] = index[begin2++];}for(int i = begin; i < end; ++i){nums[i] = tmp1[i];index[i] = tmp2[i];}}
};
2.2.4 翻转对
题目链接
493. 翻转对 - 力扣(LeetCode)
题目描述

算法原理

编写代码
class Solution {vector<int> tmp;
public:int reversePairs(vector<int>& nums) {int n = nums.size();tmp.resize(n);return MergeSort(nums, 0, n);} int MergeSort(vector<int>& nums, int begin, int end){if(end-begin < 2) return 0;//将数组从中间划分成左右两个区间int begin1 = begin;int end1 = begin1+(end-begin)/2;int begin2 = end1;int end2 = end;int cnt = 0;//分别去左右区间统计翻转对并进行排序cnt += MergeSort(nums, begin1, end1);cnt += MergeSort(nums, begin2, end2);//统计一左一右跨两个区间的翻转对int cur1 = begin1, cur2 = begin2;while(cur1 < end1 && cur2 < end2){//策略一:在cur1后面找*2都比它小的数if(nums[cur1]/2.0 > nums[cur2]) //乘法改除法,防溢出{cnt += end2-cur2; //由于是降序,所以之后的都小++cur1;}else++cur2;//策略二:在cur2前面找/2都比它大的数// if(nums[cur1]/2.0 > nums[cur2])// {// cnt += end1-cur1; //由于是升序,所以之后的都大// ++cur2;// }// else// ++cur1;}int i = begin;while(begin1 < end1 && begin2 < end2){//降序排序if(nums[begin1] >= nums[begin2]){tmp[i++] = nums[begin1++];}else{tmp[i++] = nums[begin2++];}//升序排序// if(nums[begin1] <= nums[begin2])// {// tmp[i++] = nums[begin1++];// }// else// {// tmp[i++] = nums[begin2++];// }}while(begin1 < end1){tmp[i++] = nums[begin1++];}while(begin2 < end2){tmp[i++] = nums[begin2++];}for(int i = begin; i < end; ++i){nums[i] = tmp[i];}return cnt;}
};
这篇关于【优选算法】分治 {三分快排:三指针优化,随机选key,快速选择算法;归并排序:统计数组中的逆序对,统计数组中的翻转对;相关编程题解析}的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







