三分专题
#1142 : 三分·三分求极值 （ 三分极值 ）
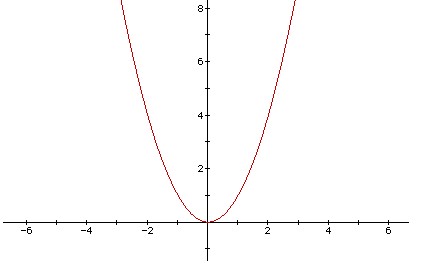
#1142 : 三分·三分求极值 时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 这一次我们就简单一点了，题目在此： [week40_1.PNG] 在直角坐标系中有一条抛物线y=ax^2+bx+c和一个点P(x,y)，求点P到抛物线的最短距离d。 提示：三分法 输入 第1行：5个整数a,b,c,x,
![[HDU 4855] Goddess （极角排序+三分）](/front/images/it_default2.jpg)
[HDU 4855] Goddess （极角排序+三分）
HDU - 4855 借这道题学了下极角排序和三分求凸函数最大值 按所有左右切线，圆心的弧度值排序，从而分割出角度上的若干个区间 射线的角度在这些区间里变动时，每个割线的长度都是凸函数，叠加起来也是凸函数 所以可以对每个区间利用三分法求得最大值，再对这些最大值取 max 即为答案 1) 利用三分法可以求得单峰函数的最大值 2) 利用 atan2(y,x)可以比较方便地求出向量与 x轴正
二分查找、三分查找求极点、二分求等比数列【模板】
二分查找： int a[110],N;int BinarySearch(int *a,int x){int Left = a[1];int Right = a[N];while(Left <= Right){int mid = (Left+Right)>>1;if(a[mid] == x)return mid;else if(a[mid] > x)Right = mid - 1;elseLe
hdu5144 三分
三分裸题，看在第三百题的份上贴一下~ #include <iostream>#include <cstring>#include <cstdio>#include <cmath>using namespace std;const double pi=acos(-1.0);const double g=9.8;double v,h;double ans(double a){doub
【分数】三兄弟分209头牛，老大分1/6，老二分2/5，老三分3/7,不能杀牛，怎么分？
1983年高考题 三兄弟分209头牛，老大分 1 6 \frac{1}{6} 61，老二分 2 5 \frac{2}{5} 52，老三分 3 7 \frac{3}{7} 73,不能杀牛，怎么分？ 解 分数加减运算 1 = 1 n 1 + 1 n 2 + 1 n 3 ⋯ + 1 n n 1=\frac{1}{n_1}+\frac{1}{n_2}+\frac{1}{n_3}\d
uva 10385 - Duathlon(三分)
题目链接：uva 10385 - Duathlon 题目大意：n个人参加铁人二项，跑步和自行车，给定总长度，以及n个人的速度。然后第n个人贿赂了举办者，所以举办者会尽量调整两个项目的长度比例，然后第n个人获胜，问第n个人可以先第二名多久。 解题思路：列出n-1个一元方程，对应成单峰函数，所以用三分求解即可。 #include <cstdio>#include <cstring>#i
uva 1476 - Error Curves(三分)
题目链接:1476 - Error Curves 题目大意：给定n条二次曲线S(x)，定义F(x)=max(Si(x)), 求出F(x)在0~1000上的最小值。 解题思路：数值方法，三分。 #include <cstdio>#include <cstring>#include <algorithm>using namespace std;const int maxn = 100
hdu 4454 Stealing a Cake(三分)
题目链接：hdu 4454 Stealing a Cake 题目大意：给定一个起始点s，一个圆形，一个矩形。现在从起点开始，移动到圆形再移动到矩形，求最短距离。 解题思路：在圆周上三分即可。即对角度[0,2*pi]三分，计算点和矩形的距离可以选点和矩形四条边的距离最短值。 #include <cstdio>#include <cstring>#include <cmath>#in
HDU 2899 Strange fuction(二分||三分)
题目链接~~> 做题感悟：这题和 2199 那题差不多。 解题思路：一、题目让求函数的最小值，首先应该分析函数图象。将函数求导得 f(x) ’ = 42 * x^6 + 48 * x^5 + 21 * x^2 + 10*x - y,因为 y 大于 0 所以假设存在 k 使f(x)'= 0,所以当0<=x<k 时f（x）’小于0,原函数在0<=x<k单调递减。在 k<x<=100 单调递增。
【优选算法】分治 {三分快排：三指针优化，随机选key，快速选择算法；归并排序：统计数组中的逆序对，统计数组中的翻转对；相关编程题解析}
一、经验总结 1.1 三分快排 优化一：三指针优化 之前学习的快速排序无法妥善处理相等或重复序列的排序问题（有序且三数取中无效），使快速排序的效率无法达到最优。 为了解决重复序列的问题，我们将原先的双指针法（前后指针）优化为三指针，将数组划分成三块： [0, left]：< key[left+1, right-1]：==key[riight, n-1]：> key其中left标记<key
![网课：第四章二分、三分、01分数规划---[USACO 2010 Feb S]Chocolate Eating](https://img-blog.csdnimg.cn/direct/f464f0f2a32d4479ae638bb9cb25e468.png)
网课：第四章二分、三分、01分数规划---[USACO 2010 Feb S]Chocolate Eating
题目 贝西收到了N（1 <= N <= 50,000）块巧克力，但她不想吃得太快，因此她想为接下来的D（1 <= D <= 50,000）天制定巧克力食用计划，以便在那些天中最大化她的最低幸福水平。 贝西的幸福水平是一个整数，起始值为0，在夜间睡觉时减半（如果必要的话向下取整）。然而，当她吃掉第i块巧克力时，她的幸福水平增加了整数 Hi （1 <= Hi <= 1,000,000）。如果她在一天
探索的时光 （整数三分）
本题链接：登录—专业IT笔试面试备考平台_牛客网 题目： 样例： 输入 53 2 1 2 3 输出 28 思路： 根据题意，已经给出了运算函数 当我们看到这些函数的时候，联想一下，它们的单调性，以及性质。这是一个抛物线，题目要求我们寻找最小值，说明就是要我们寻找极小值，寻找极值，我们使用三分。 代码详解如下： #include <iostream>#in
POJ 3737 UmBasketella(三分）
题意：给出圆锥的表面积（包含底面）。求其最大体积，以及此时的底面半径及高 #include <cmath>#include <iostream>using namespace std;#define eps 0.00000005#define PI acos(-1.0) // PI用反三角函数比较准确int main(){double s;while ( scanf("%lf"
POJ 3301 Texas Trip (三分求极限）
题意：给出许多点的坐标，用最小的正方形覆盖之。 题解：三分。注意精度····。公式神马的画个图推一下即解决 double mid1 = (left + right)/2; double mid2 = (mid1 + right)/2; 相比 double mid1 =left +(right - left)/3; double mid2 =
HDU 2438 Turn the corner 三分
题意：给一些几何数据，问车能不能过去。 想法： 由图可知，只要先确定y0=Y，那么可以求得x0然后比较x0和-Y的大小，如果x0大于-Y，表示可以通过这个角度。 #include<iostream>#include<cstdio>#include<cstring>#include<cmath>#define pi acos(-1.0)#define eps 1e-9
HDU 4717 The Moving Points 水三分
题意：有n个点，每个点朝着不同的方向按照一定的速度前进，在某个时间后，点停下来，可以求得此时任意两点之间的最大距离。问何时停止可以使得任意两点之间的最大距离最小。 想法：三分时间，判断条件是求出k时间情况下，任意两点之间的最大距离就好了。 #include<iostream>#include<cstring>#include<cstdio>#include<cmath>
HDU 3756 Dome of Circus 三分
题意：在一个三维坐标中，有n个点（x，y，z），现在要用一个圆锥曲面（z>0）去覆盖住所有的点，点在圆锥曲面上也认为是覆盖。问当z=0时，圆锥曲面的半径和当（x，y=0）时，圆锥曲面的高为多少时？圆锥曲面的体积最小。 想法：首先先看二维图，设一个线段（x,0）<->（x,y），如果此时在x外围处有一个点为k，那么很显然当k越接近x时，则k与（x,y）构成的之间与y轴的交点越是大。所以当我们
HDU 2899 Strange fuction 水三分
<strong><span style="font-family:Comic Sans MS;font-size:24px;">题意不说了，思想就是三分很朴素</span></strong> #include<iostream>#include<stdio.h>#include<string.h>#define eps 1e-9using namespace std;double a;
祝福中国 地球人类三分天下： 太土好！！！
谭理事 引子：这世界似红颜，最终命如纸薄？！不过我想，再薄也有着色的地方。不色戒，就非非想，终成无色界？ 时间之箭 除了物理圣经，即热力学第二定律外，其它物理定律是没有时间方向的。 而网上说，“依据那『时间之箭』正指向下，若热力学第二定律继续作用下去，这个宇宙到了时候就会『死去』。” 这与我们观察到的现像不一致。其关键在于热力学第二定律作
zoj 4041 Chasing(三分)
http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=4041 如果需要再一个抛物线的函数中找到最高点，就需要三分了。 这道题同理 #include<iostream>#include<cmath>#include<cstring>#include<cstdio>using namespace std;
BZOJ 1857 [Scoi2010]传送带 三分套三分
Description 在一个2维平面上有两条传送带，每一条传送带可以看成是一条线段。两条传送带分别为线段AB和线段CD。lxhgww在AB上的移动速度为P，在CD上的移动速度为Q，在平面上的移动速度R。现在lxhgww想从A点走到D点，他想知道最少需要走多长时间 Input 输入数据第一行是4个整数，表示A和B的坐标，分别为Ax，Ay，Bx，By 第二行是4个整数，表示C和D的坐标
梅需逊雪三分白，雪却输梅一段香
淡紫色的风信子 蓝莲花 雪绒花 仙人掌 薰衣草 桔梗花 满天星 星辰花 紫丁香 四叶草 铃兰 蒲公英 莲花 樱花 文心兰 忍冬花 紫罗兰 栀子花 剑兰 白山茶茶花
梅须逊雪三分白，雪却输梅一段香——CSS动画与JavaScript动画
CSS动画并不是绝对比JavaScript动画性能更优越，开源动画库Velocity.js等就展现了强劲的性能。 一、两者的主要区别 先开门见山的说说两者之间的区别。 1）CSS动画： 基于CSS的动画一般由浏览器“主线程”之外的独立线程处理，在其中执行样式、布局、绘制和 JavaScript。 使用CSS动画，允许对单个动画关键帧、持续时间和迭代进行更多控制。 但缺乏表现力，并且很难有意义地组