本文主要是介绍模拟退火+三分,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目
题解
方法一:三分套三分(两个变量x和y的单峰函数,二维的三分法求解)
#include<bits/stdc++.h>
using namespace std;
int n;
double xx[1005],yy[1005],w[1005];double lx,rx,ly,ry;double dis(double x1,double y1,double x2,double y2){return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}double work(double x,double y){double ans=0;for(int i=1;i<=n;i++){ans+=w[i]*dis(x,y,xx[i],yy[i]);}return ans;
}double three(double x){ly=-10000.0;ry=10000.0;for(int i=1;i<=100;i++){double d=(ry-ly)/3.0;double zuo=ly+d;double you=ry-d;double zuo_val=work(x,zuo);double you_val=work(x,you);if(zuo_val<=you_val)ry=you;else ly=zuo;}return work(x,ly);
}int main(){cin>>n;for(int i=1;i<=n;i++){//cin>>xx[i]>>yy[i]>>w[i];scanf("%lf%lf%lf",xx+i,yy+i,w+i);}lx=-10000.0,rx=10000.0;for(int i=1;i<=100;i++){double d=(rx-lx)/3.0;double zuo=lx+d;double you=rx-d;double zuo_val=three(zuo);double you_val=three(you);if(zuo_val<=you_val)rx=you;else lx=zuo;}printf("%.3f %.3f",lx,ly);
}
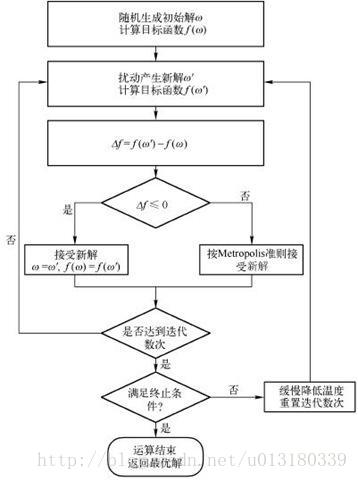
方法二:模拟退火
将热力学的东西运用到状态学上
(1) 温度T的初始值设置问题。 温度T的初始值设置是影响模拟退火算法全局搜索性能的重要因素之一、初始温度高,则搜索到全局最优解的可能性大,但因此要花费大量的计算时间;反之,则可节约计算时间,但全局搜索性能可能受到影响。实际应用过程中,初始温度一般需要依据实验结果进行若干次调整。
(2) 退火速度问题。 模拟退火算法的全局搜索性能也与退火速度密切相关。一般来说,同一温度下的“充分”搜索(退火)是相当必要的,但这需要计算时间。实际应用中,要针对具体问题的性质和特征设置合理的退火平衡条件。
(3) 温度管理问题。 温度管理问题也是模拟退火算法难以处理的问题之一。实际应用中,由于必须考虑计算复杂度的切实可行性等问题,常采用如下所示的降温方式:式中k为正的略小于1.00的常数,t为降温的次数。 !
#include<bits/stdc++.h>
using namespace std;
#define begin_T 10000
#define end_T 1e-8
#define change_T 0.99
int n;
double xx[1001],yy[1001],w[1001],ansx,ansy;
double ans_e;
double energy(double x,double y){double res=0;for(int i=1;i<=n;i++){res+=w[i]*sqrt( (x-xx[i])*(x-xx[i]) +(y-yy[i])*(y-yy[i]) );}return res;
}
void sa(int times){while(times--){for(double t=10000;t>1e-14;t*=0.999){//在当前的最优解ansx,ansy上波动寻找更优解//随着温度的减小,波动幅度也变小double dx=ansx+(2*rand()-RAND_MAX)*t;double dy=ansy+(2*rand()-RAND_MAX)*t;double now_e=energy(dx,dy);if(now_e<ans_e){ansx=dx;ansy=dy;ans_e=now_e;}else if(exp( (ans_e-now_e)/t) >double(rand())/RAND_MAX ){ansx=dx;ansy=dy;//ans_e=now_e;}}}
}
int main(){//cout<<ans_e<<endl;//srand(time(0));cin>>n;for(int i=1;i<=n;i++){cin>>xx[i]>>yy[i]>>w[i];ansx+=xx[i];ansy+=yy[i];}//将答案初始化为平均数ansx/=n;ansy/=n;ans_e=energy(ansx,ansy);//cout<<"ans_e="<<ans_e<<endl;sa(4);printf("%.3f %.3f\n",ansx,ansy);//cout<<"ans_e="<<ans_e<<endl;}
这篇关于模拟退火+三分的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!