754专题
C语言_浮点数_IEEE 754标准_单片机_浮点数精度
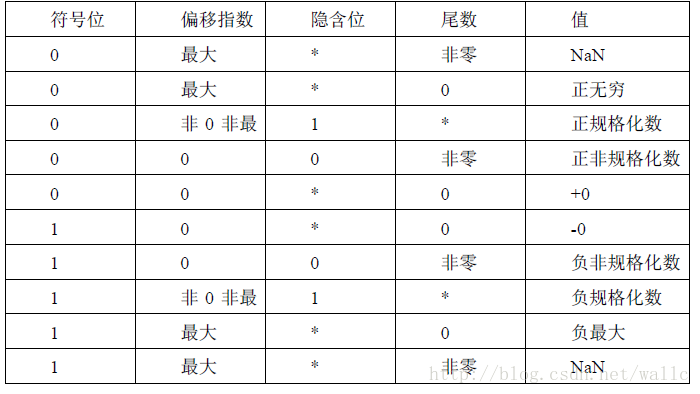
目录 IEEE 754标准 float的范围 float精度 float小数 读取小数存储的原始值(举例) IEEE 754标准 浮点格式可分为符号位s,指数位e以及尾数位f三部分。 其中真实的指数E相对于实际的指数有一个偏移量,所以E的值应该为e-Bias,Bias(127)即为指数偏移量。这样做的好处是便于使用无符号数来代替有符号的真实指数。尾数f字段代表纯粹的小
**Leetcode 754. Reach a Number | 拼多多笔试第三题
https://leetcode.com/problems/reach-a-number/description/ 开始一直手残,,target=-target这行代码 写了,但是符号忘记带了。。 class Solution {public:long long cal( long long n, long long target ) {long long ret = (n *
IEEE 754 的标准对浮点数的处理
参考文章: https://blog.csdn.net/weixin_42066185/article/details/88559936 作者在工作中现在就面临这个浮点数通过modbus协议向上位机传输的问题的存在,遇到的是,我们应该怎么样合适的处理这个float 4个bytes 的数据,下面总结一下 个人的调研的结果: 通过网上的调研结果有下面的两种的解决的方案: 方案一:通过将
acwing——754. 平方矩阵 II
754. 平方矩阵 II 输入整数N,输出一个N阶的二维数组。 数组的形式参照样例。 输入格式 输入包含多行,每行包含一个整数N。 当输入行为N=0时,表示输入结束,且该行无需作任何处理。 输出格式 对于每个输入整数N,输出一个满足要求的N阶二维数组。 每个数组占N行,每行包含N个用空格隔开的整数。 每个数组输出完毕后,输出一个空行。 数据范围 0≤N≤1000≤N≤100
1536. 排布二进制网格的最少交换次数;754. 到达终点数字;1106. 解析布尔表达式
1536. 排布二进制网格的最少交换次数 核心思想:贪心。枚举每一行,然后去找离这行最近的满足要求的那一行。我们用j保存每一行的最后一个1,那么尾部的0个数为n-1-j,每一行需要的0个数为n-i-1,所以得出结论 i >= j。然后我们就去一行一行找,找到了就翻转,这里有个小技巧,就是在枚举每一行的时候用一个k=-1表示,如果最后k还为-1就没有找到。 754. 到达终点数字 核心
leetcode 754. Reach a Number | 754. 到达终点数字(数学问题)
题目 https://leetcode.com/problems/reach-a-number/ 题解 一看数据规模,再看踩的数量,觉得这题不一般。。 只能想出暴力解,不用试了,肯定超时。没有想到如何 dp(dp 即便可以,O(n) 应该也会超时) 看了 答案,这是个数学问题。 时隔两天,重新理了下思路,然后实现了一下: class Solution {public int
浮点数的转换--IEEE 754
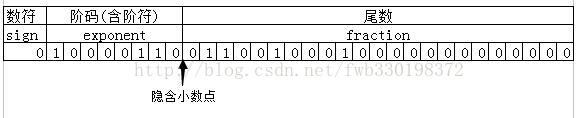
IEEE754标准是一种浮点数表示标准,一般分为 单精度(32位的二进制数);双精度(64位的二进制数) 根据国际标准IEEE754,任意一个二进制浮点数V可以表示为下面形式: V = (-1)^s *(1+M)* 2^(E-127)(单精度)V = (-1)^s *(1+M)* 2^(E-1023)(双精度) 其中,E为阶码位,M为尾数部分,S为符号位; M: 1<=M<2, 即M写成
浮点数的转换--IEEE 754
IEEE754标准是一种浮点数表示标准,一般分为 单精度(32位的二进制数);双精度(64位的二进制数) 根据国际标准IEEE754,任意一个二进制浮点数V可以表示为下面形式: V = (-1)^s *(1+M)* 2^(E-127)(单精度)V = (-1)^s *(1+M)* 2^(E-1023)(双精度) 其中,E为阶码位,M为尾数部分,S为符号位; M: 1<=M<2, 即M写成
Leetcode 754. Reach a Number [Python]
先来一个BFS吧,可以想做一个binary tree,root是0.左侧子树是0-1,右侧是0+1.然后每一层的边的权重比上一层+1.也就是第二层节点是-1,1,其左子是 - 1 -2,-1+2以及1-2和1+2. 找到target时,返回层数-1.这样做会TLE。 class Solution:def reachNumber(self, target: int) -> int:level =
Leetcode 754. Reach a Number [Python]
先来一个BFS吧,可以想做一个binary tree,root是0.左侧子树是0-1,右侧是0+1.然后每一层的边的权重比上一层+1.也就是第二层节点是-1,1,其左子是 - 1 -2,-1+2以及1-2和1+2. 找到target时,返回层数-1.这样做会TLE。 class Solution:def reachNumber(self, target: int) -> int:level =
754. Reach a Number
754. 到达终点数字 在一根无限长的数轴上,你站在0的位置。终点在target的位置。 每次你可以选择向左或向右移动。第 n 次移动(从 1 开始),可以走 n 步。 返回到达终点需要的最小移动次数。 示例 1: 输入: target = 3输出: 2解释:第一次移动,从 0 到 1 。第二次移动,从 1 到 3 。 示例 2: 输入: target = 2输出: 3解
Leetcode 754. 到达终点数字
Leetcode 754. 到达终点数字 1. 问题描述 2. 思路 纯粹 数学找规律问题 3. 代码 class Solution {public int reachNumber(int target) {target = Math.abs(target);int k = 0;while (target > 0) {k++;target = target - k;}if (tar
LeetCode-754. 到达终点数字【数学】
LeetCode-754. 到达终点数字【数学】 题目描述:解题思路一:三行代码。发现规律,将target取绝对值不影响结果。若未到达终点继续走即可。情况一:若最后s-target为偶数或0,我们发现可以在之前里面反走一步即可(答案刚刚好是n)。情况二:若s-target为奇数,则需要多走一步或者两步,所以while里面取的是或操作。解题思路二:判断s大于等于target时可以解方程。n*(
【Leetcode 754】到达终点数字
Leetcode 题录 - 2022/11/04 754. 到达终点数字题目图解代码 754. 到达终点数字 题目 在一根无限长的数轴上,你站在0的位置。终点在target的位置。 你可以做一些数量的移动 numMoves : 每次你可以选择向左或向右移动。 第i次移动(从 i == 1 开始,到 i == numMoves ),在选择的方向上走i步。 给定整数 targ
详解IEEE 754标准(浮点数的二进制表示)
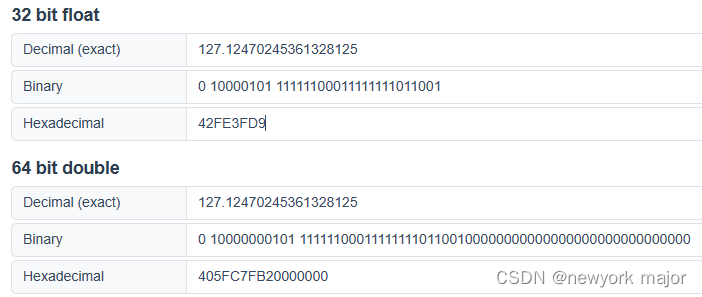
浮点数是我们在程序里常用的数据类型,它在内存中到底是怎么样的形式存在,是我了解之前是觉得好神奇,以此记录,作为学习笔记。 现代计算机中,一般都以IEEE 754标准存储浮点数,这个标准的在内存中存储的形式为: 对于不同长度的浮点数,阶码与小数位分配的数量不一样,如下: 对于32位的单精度浮点数,数符分配是1位,阶码分配了8位,尾数分配了是23位。 根据这个标准,我们来尝试把一个十进制的
IEEE 754 和python
今天遇到了一个问题 arange范围不是左闭右开吗,怎么回事 然后发现是浮点数的锅,由于精度问题,浮点数是不准确的,比如 这就是导致上述问题的原因。 那只好用decimal了
LeetCode 754. 到达终点数字java
在一根无限长的数轴上,你站在0的位置。终点在target的位置。 每次你可以选择向左或向右移动。第 n 次移动(从 1 开始),可以走 n 步。 返回到达终点需要的最小移动次数。 示例 1: 输入: target = 3输出: 2解释:第一次移动,从 0 到 1 。第二次移动,从 1 到 3 。 示例 2: 输入: target = 2输出: 3解释:第一次移动,从 0