本文主要是介绍浮点数的转换--IEEE 754,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
IEEE754标准是一种浮点数表示标准,一般分为
- 单精度(32位的二进制数);
- 双精度(64位的二进制数)
根据国际标准IEEE754,任意一个二进制浮点数V可以表示为下面形式:
- V = (-1)^s *(1+M)* 2^(E-127)(单精度)
- V = (-1)^s *(1+M)* 2^(E-1023)(双精度)
其中,E为阶码位,M为尾数部分,S为符号位;
- M: 1<=M<2, 即M写成1.xxxxx形式;
- EEE 754规定,计算机内部保存M它的第一位总是1,因此可以只保存后面的xxxxxx部分。如1.001时,尾数001,需要读取时,再把第一位的1加上去。这样做可以节省1位有效数字;
- E:无符号整数,如果E为8位,其取值范围为0~255;若E为11位,取值范围为0~2047
- 科学计数法中,E可以是负数,因此,IEEE 754规定,E的真实值必须再减去一个中间数,对于8位的E,这个中间数是127;对于11位的E,这个中间数是1023;
- e.g. 2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001。
- 特殊处理:
- E不全为0或1时,浮点数就采用上面的规则表示,即指数E的计算值减去127(或1023),得到真实值,再将有效数字M前加上第一位的1;
- E全为0时,浮点数的指数E等于1-127(或者1-1023),有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数。这样做是为了表示±0,以及接近于0的很小的数字;即:V = (-1)^s *(M)* 2^(1-127)
- E全为1时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s);如果有效数字M不全为0,表示这个数不是一个数(NaN)
下面以32bits的浮点数为例子:
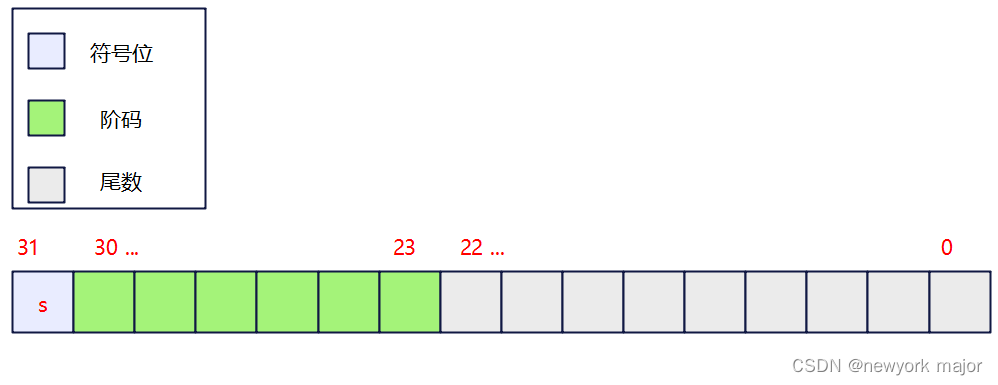
将十进制数0.15625转换为浮点数:
1. 将对应数据逐步乘以2,取整数部分;
⭘0.15625x2=0.3125 取整0
⭘0.31250x2=0.6250 取整0
⭘0.62500x2=1.2500 取整1
⭘0.25000x2=0.5000 取整0
⭘0.50000x2=1.0000 取整1
2. 将整数部分进行组合,得到0.00101;
3. 将得到的数,表示成IEEE 754的格式,0.00101=1.01*2-3
4. 将该数据,与公式进行对比,可以得出:1.01*2**-3 = (-1)s * (1+M)*2**(E-127), 可以得出:
⭘s=0;
⭘1+M=1.01, M=0.01;
⭘E-127=-3, E=124; 124 = BIN 0111 1100
5. 将上述的值,填入到32bits的范围内,可得:

使用上面的方式,转换十进制数-0.0625:
DEC -0.0625 = BIN -0.0001 = -1.0*2-4 s=1,M=1-1=0,E=-4 +127=123=0111 1011

使用上面的方式,转换十进制数127.1247:
这个数可能在32bits范围内,不能准确的表示出来,因此需要进行截位;
按照上面的公式,整数部分,127: 0111_1111;
小数部分:0.1247,不断乘以2,取整数部分,00011111111011001..., 因为位数不够,进行截断;
转换成上面的公式可以得到:M=1.11111100011111111011001,E=127+6=133, 所以转换后的浮点数为:
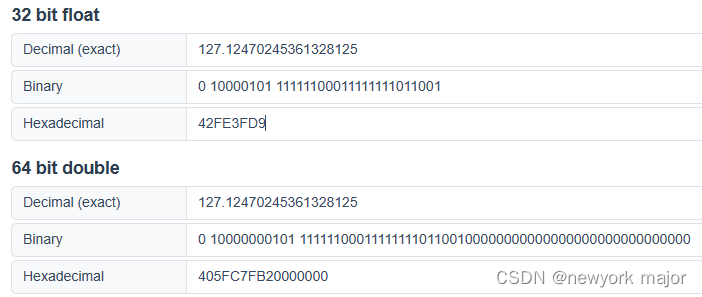
附上IEEE 754在线转换工具:
IEEE 754 浮点数 - 在线工具 (toolhelper.cn)
这篇关于浮点数的转换--IEEE 754的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






