本文主要是介绍C语言_浮点数_IEEE 754标准_单片机_浮点数精度,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
IEEE 754标准
float的范围
float精度
float小数
读取小数存储的原始值(举例)
IEEE 754标准
浮点格式可分为符号位s,指数位e以及尾数位f三部分。
其中真实的指数E相对于实际的指数有一个偏移量,所以E的值应该为e-Bias,Bias(127)即为指数偏移量。这样做的好处是便于使用无符号数来代替有符号的真实指数。尾数f字段代表纯粹的小数,它的左侧即为小数点的位置。规格化数的隐藏位默认值为1,不在格式中表达。
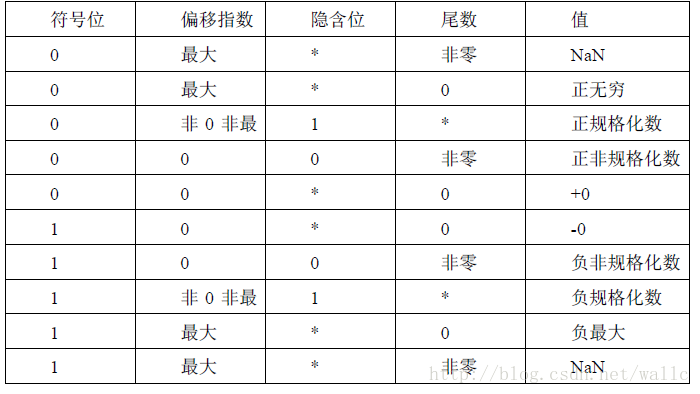
在IEEE-754 标准下,浮点数一共分为:
- NaN:即Not a Number。非数的指数位全部为1 同时尾数位不全为0。在此前提下,根据尾数位首位是否为1,NaN 还可以分为SNaN 和QNaN 两类。前者参与运算时将会发生异常。
- 无穷数:指数位全部为1 同时尾数位全为0。大。
- 规格化数:指数位不全为1 同时尾不全为0。此时浮点数的隐含位有效,其值为1。
- 非规格化数:指数位全为0 且尾数位不全为0。此时隐含位有效值变为0。另外需要注意,以单精度时为例,真实指数e并非0-127=-127,而是-126,这样一来就与规格化下最小真实指数e=1-127=-126 达成统一,形成过渡。非规格化数隐函位表示为了0,此时表示的数据更小,提高了精度(0.1和1.1,隐含位是0的表示的更小)。
- 0 :指数位与尾数位都全为0,根据符号位决定正负。
float的范围
注意:指数的范围是-126~127,不是我们认为的-127~128 ,这个是IEEE-754标准中定义的。
(1)正数最大值如下:
高地址----------------------------->低地址
0 (1111 1110)( 111 1111 1111 1111 1111 1111)
当我们令指数位为:1111 1110 =254 (此处不能是1111 1111=255,1111 1111是NaN),则指数为254-127=127
尾数位全为1,则最大数为1.11111111111111111111111*2^127=(2-2^-23)*2^127=3.4028*10^38,正规格化数中的最大。其中1.111 1111 1111 1111 1111 1111+ 0.000 0000 0000 0000 0000 0001=2,0.000 0000 0000 0000 0000 0000=2-2^{-23}
当符号位为1时,是表示绝对值最大的负数
高地址----------------------------->低地址
1(1111 1110)( 111 1111 1111 1111 1111 1111)
表示-3.40*10^38
所以范围是-3.40*10^38 到 3.40*10^38
(2) float最小值(除0以外的最小值)
高地址----------------------------->低地址
0 (0000 0001)(000 0000 0000 0000 0000 0001)
当我们令指数位为:0000 0001 =1(此处不能是0000 0000=0,指数全零是非规格化数)则指数为1-127=126
为:1.0000 0000 0000 0000 0000 001*2^-126= 1.175e-038
float精度
float 类型的数据精度取决于尾数,首先是在不考虑指数的情况下23位尾数能表示的范围是[0, 2^23−1],实际上尾数位前面还隐含了一个"1",所以应该是一共24位数字,所能表示的范围是[0, 2^24-1](因为隐含位默认是"1",所以表示的数最小是1不是0),看到这24位能表示的最大数字为2^{24}-1,换算成10进制就是16777215,那么[0, 16777215]都是能精确表示的
16777215 这个数字可以写成1.1111111 11111111 1111111 * 2^{23},所以这个数可以精确表示,然后考虑更大的数16777216,因为正好是2的整数次幂,可以表示1.0000000 00000000 00000000 * 2^{24}所以这个数也可以精确表示,在考虑更大的数字16777217,这个数字如果写成上面的表示方法应该是 1.0000000 00000000 00000000 1 * 2^{24},但是这时你会发现,小数点后尾数位已经是24位了,23位的存储空间已经无法精确存储,这时浮点数的精度问题也就是出现了。
看到这里发现 16777216 貌似是一个边界,超过这个数的数字开始不能精确表示了,那是不是所有大于16777216的数字都不能精确表示了呢?其实不是的,比如数字 33554432 就可以就可以精确表示成1.0000000 00000000 00000000 * 2^{25},说到这里结合上面提到的float的内存表示方式,我们可以得出大于 16777216 的数字(不超上限),只要可以表示成小于24个2的n次幂相加,并且每个n之间的差值小于24就能够精确表示。换句话来说所有大于 16777216 的合理数字,都是[0, 16777215]范围内的精确数字通过乘以2^n得到的,同理所有小于1的正数,也都是 [0, 16777215] 范围内的精确数字通过乘以2^n得到的,只不过n取负数就可以了。
16777216 已经被证实是一个边界,小于这个数的整数都可以精确表示,表示成科学技术法就是1.6777216 * 10^{7},从这里可以看出一共8位有效数字,由于最高位最大为1不能保证所有情况,所以最少能保证7位有效数字是准确的,这也就是常说float类型数据的精度。
float小数
从上面的分析我们已经知道,float可表示超过16777216范围的数字是跳跃的,同时float所能表示的小数也都是跳跃的,这些小数也必须能写成2的n次幂相加才可以,比如0.5、0.25、0.125…以及这些数字的和,像5.2这样的数字使用float类型是没办法精确存储的,5.2的二进制表示为101.0011001100110011001100110011……最后的0011无限循环下去,但是float最多能存储23位尾数,那么计算机存储的5.2应该是101.001100110011001100110,也就是数字 5.19999980926513671875,计算机使用这个最接近5.2的数来表示5.2。关于小数的精度与刚才的分析是一致的,当第8位有效数字发生变化时,float可能已经无法察觉到这种变化了。
读取小数存储的原始值(举例)
stm32 中小数存储计算
counter+=0.001;
if(counter==0.01)//该条件永远不会成立,十进制小数转换二进制的问题导致,应该转换为大于等于或者小于等于
asda=*(vu32*)&counter;可通过该句读取counter在内存中的存储的数据;
asda=*(vu32*)&counter;取counter地址,指针类型强制转换成vu32*,然后*取内容。
0.01为0x3C23D70A,转换成2进制
0011 1100 0010 0011 1101 0111 0000 1010
符号位 0 代表正数
指数011 1100 0 为120 (120-127)=-7,小数点左移动7。(如果是130则130-127=3,表示小数点右移动三位。)
尾数01000111101011100001010 左边有一个可以理解的二进制点。此数字从浮点数的存储形式中省略。在尾数的开头加上1和二进制点可得到以下值:
1.0100 0111 1010 1110 0001 0100 左移7位为0.0000 0010 1000 1111 0101 1100 0010 1000
http://www.ab126.com/system/7348.html (带小数的二进制转换十进制计算器的网址)
转换为十进制0.00999999977648258
实际在watch窗口中观察写入0.01为0.00999999978(被四舍五入了)
参考链接:https://blog.csdn.net/albertsh/article/details/92385277
这篇关于C语言_浮点数_IEEE 754标准_单片机_浮点数精度的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!