343专题
代码随想录:343. 整数拆分
343. 整数拆分 class Solution {public:int integerBreak(int n) {int dp[100]={0};//拆分i的最大乘积为dp[i]dp[1]=1;//初始化,主要是为了dp[2]初始for(int i=2;i<=n;i++){for(int j=1;j<i;j++){ dp[i]=max(dp[i],max(j,dp[j])*ma
【动态规划】343. 整数拆分
力扣链接:343. 整数拆分 - 力扣(LeetCode) dp数组的含义:dp[i]表示对i拆分,得到最大的积为dp[i] 递推公式:拆成两个数是 j*(i-j),拆成三个及以上是 j*dp[i-j],所以递推公式取两者大值 遍历顺序:从小到大 public int integerBreak(int n) {int[] dp = new int[n+1];dp[1]=0;dp[2]=
代码随想录训练营day34|62.不同路径,63. 不同路径 II,343.整数拆分,96.不同的二叉搜索树
不同路径1 题目 题目并不难想,每一个点只有两种走到的方法,要么从左侧来,要么从上侧来,所以 dp[i][j]=dp[i-1][j]+dp[i][j-1]; vector<vector<int>> dp(m,vector<int>(n,0)); for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(i>0&&j>0){dp[i][j]=dp[i-1][
DP-343. 整数拆分
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。 示例 1: 输入: n = 2输出: 1解释: 2 = 1 + 1, 1 × 1 = 1。 示例 2: 输入: n = 10输出: 36解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。 提示: 2 <= n <=
力扣(动态规划)-343整数拆分;96不同的二叉搜索树
整数拆分 题目: 给定⼀个正整数 n,将其拆分为⾄少两个正整数的和,并使这些整数的乘积最⼤化。 返回你可以获得的最⼤乘积。 示例 1: 输⼊: 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1。 示例 2: 输⼊: 10 输出: 36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。 提示: 2 <= n <= 58 说明: 你
代码随想录算法训练营第三十九天|62.不同路径 63. 不同路径 II 343.整数拆分 96.不同的二叉搜索树
LeetCode 62.不同路径 题目链接:62.不同路径 踩坑:二维的vector数组需要初始化,否则会报错访问空指针 思路: 确定动态数组的含义:dp[i][j]:到达(i,j)有多少条路经递推公式:dp[i][j] = dp[i-1][j] + dp[i][j-1]初始化动态数组:dp[0][0] = 1遍历顺序:从左到右,从上到下 代码: class Solution {pu
动态规划02(Leetcode62、63、343、96)
参考资料: https://programmercarl.com/0062.%E4%B8%8D%E5%90%8C%E8%B7%AF%E5%BE%84.html 62. 不同路径 题目描述: 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
代码随想录算法训练营Day39|62.不同路径、63.不同路径II、343.整数拆分、96.不同的二叉搜索树
不同路径 62. 不同路径 - 力扣(LeetCode) 机器人位于m*n网格的左上角,机器人每次只能向下或向右移动一步(移动方向只有下和右,固定了不能回返路径)。机器人需要达到网格的右下角,需要得到共有多少条路径。 思路:使用动态规划来解决,这里需要得到动态规划的dp矩阵,以及dp矩阵的推演公式。 这里我们假定dp矩阵为m*n的矩阵,dp[i][j]为能抵达 i -1,j-1的路径总数,
leetcode打卡#day42 62. 不同路径、63. 不同路径 II、343. 整数拆分、96. 不同的二叉搜索树
62. 不同路径 class Solution {public://动态规划int uniquePaths(int m, int n) {//dp数组,记录到达目的地的路径数vector<vector<int>> dp(m, vector(n, 0));//初始化for(int i=0; i< m; i++) dp[i][0] = 1;for(int i=0; i< n; i++) dp[0]
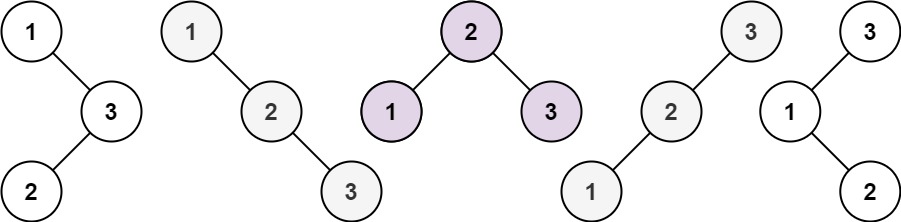
● 343. 整数拆分 ● 96.不同的二叉搜索树
343. 整数拆分 给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。 示例 1: 输入: n = 2输出: 1解释: 2 = 1 + 1, 1 × 1 = 1。 示例 2: 输入: n = 10输出: 36解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。 cla
【代码随想录训练营】【Day 43】【动态规划-3】| Leetcode 343, 96
【代码随想录训练营】【Day 43】【动态规划-3】| Leetcode 343, 96 需强化知识点 思路:343 and 96 题目 343. 整数拆分 dp 含义:拆分i,乘积最大值;依次遍历 i的因子,记录最大值,max(之前的因子,两两拆分的情况,多次拆分的情况) class Solution:def integerBreak(self, n: int) -> int:# 拆
代码随想录算法训练营day43 | 343. 整数拆分、96.不同的二叉搜索树
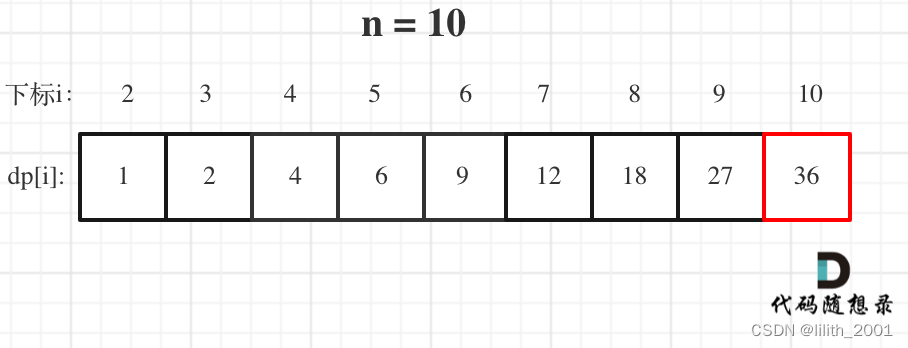
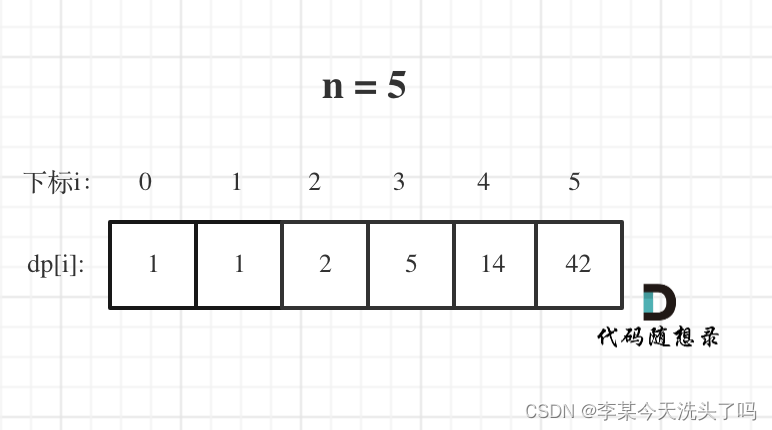
343. 整数拆分 确定dp数组以及下标的含义:dp[i]表示分拆数字i的最大乘积确定递推公式:dp[i] = max(dp[i], max(i - k) * k, dp[i - k] * k});dp的初始化:dp[0]和dp[1]都是没有意义的,纯粹是为了后续遍历服务的确定遍历顺序:从前向后遍历举例推导dp数组 class Solution:def integerBreak(self, n
代码随想录算法训练营第四十三天 | 343. 整数拆分、96.不同的二叉搜索树
343. 整数拆分 代码随想录 视频讲解:动态规划,本题关键在于理解递推公式!| LeetCode:343. 整数拆分_哔哩哔哩_bilibili 解题思路 1. dp[i]对i进行拆分,得到的最大的乘积为dp[i] 2.递推公式 一个是j * (i - j) 直接相乘,拆为两个数 一个是j * dp[i - j],相当于是拆分(i - j),拆为三个或以上 dp[
代码随想录算法训练营第40天|● 343. 整数拆分 ● 96.不同的二叉搜索树
343. 整数拆分 动归 递归拆 class Solution:def integerBreak(self, n: int) -> int:dp=[0]*(n+1)dp[2]=1for i in range(3,n+1):for j in range(1,i//2+1):dp[i]=max(dp[i],(i-j)*j,dp[i-j]*j)return dp[n] 公式:全拆3,剩1个4
算法训练Day35 | ● 343. 整数拆分 ● 96.不同的二叉搜索树
343. 整数拆分 class Solution {public:int integerBreak(int n) {vector<int> dp(n+1, 0);dp[2] = 1;for(int i=3; i<n+1; i++){for(int j= 1; j<=i/2; j++){dp[i] = max(dp[i], max(j*(i-j), j*dp[i-j]));}}return d
60500 - Error 343 when transf. fixed assets w/o inv.support
错误消息 AA343“报废和接收资产在范围 xy 中具有差异投资代码”错误出现,即使不管理折旧范围 xy 中投资支持的固定资产将转移到管理此范围内投资支持的固定资产。 Tcode: AB01、ABUM 原因和前提条件 源代码检入过于严格。 解决方案 应用此notes
代码随想录算法训练营DAY40\DAY41|C++动态规划Part.3|343.整数拆分、96.不同的二叉搜索树
DAY40休息日,本篇为DAY41的内容 文章目录 343.整数拆分思路dp含义递推公式(难点)初始化遍历顺序打印 CPP代码数学方法归纳证明法 96.不同的二叉搜索树思路dp含义递推公式初始化遍历顺序打印 CPP代码题目总结 343.整数拆分 力扣题目链接 文章讲解:343.整数拆分 视频讲解:动态规划,本题关键在于理解递推公式!| LeetCode:343. 整数拆分 状
代码随想录第40天|343. 整数拆分
343. 整数拆分 343. 整数拆分 - 力扣(LeetCode) 代码随想录 (programmercarl.com) 动态规划,本题关键在于理解递推公式!| LeetCode:343. 整数拆分_哔哩哔哩_bilibili 给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。 示例 1: 输入: n =
代码随想录算法训练营第四十一天| 343. 整数拆分,96.不同的二叉搜索树
题目与题解 343. 整数拆分 题目链接:343. 整数拆分 代码随想录题解:343. 整数拆分 视频讲解:动态规划,本题关键在于理解递推公式!| LeetCode:343. 整数拆分_哔哩哔哩_bilibili 解题思路: 一眼懵,直接看答案了 看完代码随想录之后的想法 前一天的题是由dp[i-2]和dp[i-1],递推出当前结果dp[i]。这
代码随想录算法训练营第四十一天|343.整数拆分、96.不同的二叉搜索树
代码随想录算法训练营第四十一天|343.整数拆分、96.不同的二叉搜索树 343.整数拆分 给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。 示例 1: 输入: n = 2输出: 1解释: 2 = 1 + 1, 1 × 1 = 1。 题解:将数字尽可能拆分成m个近似相等的子数,这样乘积才最大。
代码随想录算法训练营第四十一天| LeetCode 343. 整数拆分、96.不同的二叉搜索树
一、LeetCode 343. 整数拆分 题目链接/文章讲解/视频讲解:https://programmercarl.com/0343.%E6%95%B4%E6%95%B0%E6%8B%86%E5%88%86.html 状态:已解决 1.思路 题目的要求是要我们拆除某个给定的整数,让其拆分后的数相乘结果最大。因此我们知道此题分两步,第一步是拆分,第二步是求乘积最大值。
力扣日记4.10-【动态规划篇】343. 整数拆分
力扣日记:【动态规划篇】343. 整数拆分 日期:2024.4.10 参考:代码随想录、力扣 343. 整数拆分 题目描述 难度:中等 给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。 示例 1: 输入: n = 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1。
代码随想录day41| 343. 整数拆分 、96.不同的二叉搜索树
343. 整数拆分 dp[i]:对i进行拆分,相乘得到的最大值dp[i] 递推公式: dp[i] = max(dp[i], j * (i - j), j * dp[i - j]); 为什么还要dp[i[放进去比较? ——这其实是在不断更新dp[i]的值,不放进的话,原本的dp[i]会直接被舍弃 初始化:dp[0]和dp[1]都是没有意义的,所以初始化为零,dp[2]=1 为什么只需
[Leetcode 343]. 整数拆分 [剑指offer] 面试题14- I. 剪绳子
给定一个正整数 n,将其拆分为至少两个正整数的和,并使这些整数的乘积最大化。 返回你可以获得的最大乘积。 给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1]…*k[m-1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最