222专题
222.完全二叉树的节点个数
（写给未来遗忘的自己） 题目： 代码： class Solution {public:int countNodes(TreeNode* root) {queue<TreeNode*>node_que;if(root==nullptr) return 0;node_que.push(root);int result;while(!node_que.empty()){int layer_s
![[机缘参悟-222] - 系统的重构源于被动的痛苦、源于主动的精进、源于进化与演进（软件系统、思维方式、亲密关系、企业系统、商业价值链、中国社会、全球）](https://i-blog.csdnimg.cn/direct/fd1df13932fb4df09c34297f62f78bf0.png)
[机缘参悟-222] - 系统的重构源于被动的痛苦、源于主动的精进、源于进化与演进（软件系统、思维方式、亲密关系、企业系统、商业价值链、中国社会、全球）
目录 前言：系统的重构源于被动的痛苦、源于主动的精进、源于进化与演进 一、软件系统的重构 1、重构的定义与目的 2、重构的时机与方法 3、重构的注意事项 4、重构的案例分析 二、大脑思维的重构 1、大脑思维重构的定义 2、大脑思维重构的方法 3、大脑思维重构的挑战与前景 三、认知的重构 1、定义 2、目的 3、方法 四、实例 五、总结 四、婚姻家庭的重构 1、婚
代码随想录算法训练营第十五天| 110.平衡二叉树、257. 二叉树的所有路径、404.左叶子之和、 222.完全二叉树的节点个数
Leetcode110.平衡二叉树 题目链接：110. 平衡二叉树 C++：(后序遍历) class Solution {public:int getheight(TreeNode *node){if(node == nullptr) return 0;//左int leftheight = getheight(node->left);if(leftheight == -1) return
力扣222题详解：完全二叉树的节点个数的多种解法与模拟面试
在本篇文章中，我们将详细解读力扣第222题“完全二叉树的节点个数”。通过学习本篇文章，读者将掌握如何使用多种方法来解决这一问题，并了解相关的复杂度分析和模拟面试问答。每种方法都将配以详细的解释，以便于理解。 问题描述 力扣第222题“完全二叉树的节点个数”描述如下： 给你一棵完全二叉树的根节点，求出该树的节点个数。 完全二叉树的定义如下：在完全二叉树中，除了最后一层外，其他每一层的节点数都
代码随想录训练营第十五天 110平衡二叉树 257二叉树的所有路径 404左子树之和 222完全二叉树的节点
第一题： 原题链接：110. 平衡二叉树 - 力扣（LeetCode） 首先什么事平衡二叉树：平衡二叉树 是指该树所有节点的左右子树的深度相差不超过 1。 思路： 首先我们要定义返回值和传入的参数，传入的参数就是当前传入节点，返回值是传入节点为根节点的树的高度。 现在要标记的是左右子树的差值是否大于1，那么如果当前传入节点为根节点的二叉树已经不是儿二叉平衡树的话，还返回高度的话就没有意义
算法训练营day15--110.平衡二叉树+ 257. 二叉树的所有路径+ 404.左叶子之和+222.完全二叉树的节点个数
一、110.平衡二叉树 题目链接：https://leetcode.cn/problems/balanced-binary-tree/ 文章讲解：https://programmercarl.com/0110.%E5%B9%B3%E8%A1%A1%E4%BA%8C%E5%8F%89%E6%A0%91.html 视频讲解：https://www.bilibili.com/video/BV1Ug41
leetcode-13-[110]平衡二叉树[257]二叉树的所有路径[404]左叶子之和[222]完全二叉树的节点个数
一、[110]平衡二叉树 注意：注释的1、2两处得有返回值-1 class Solution {public boolean isBalanced(TreeNode root) {int result = getHeight(root);return result != (-1);}//高度public int getHeight(TreeNode node){if(node==null){r
222、求出完全二叉树的节点
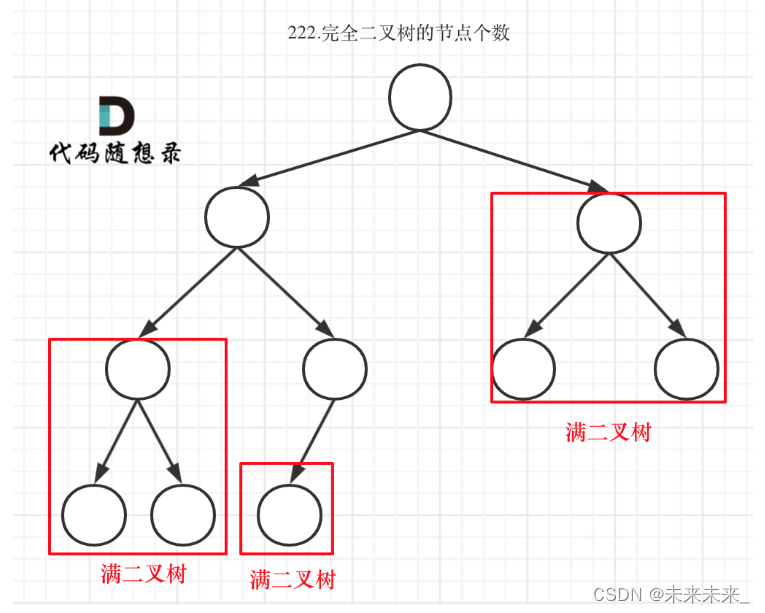
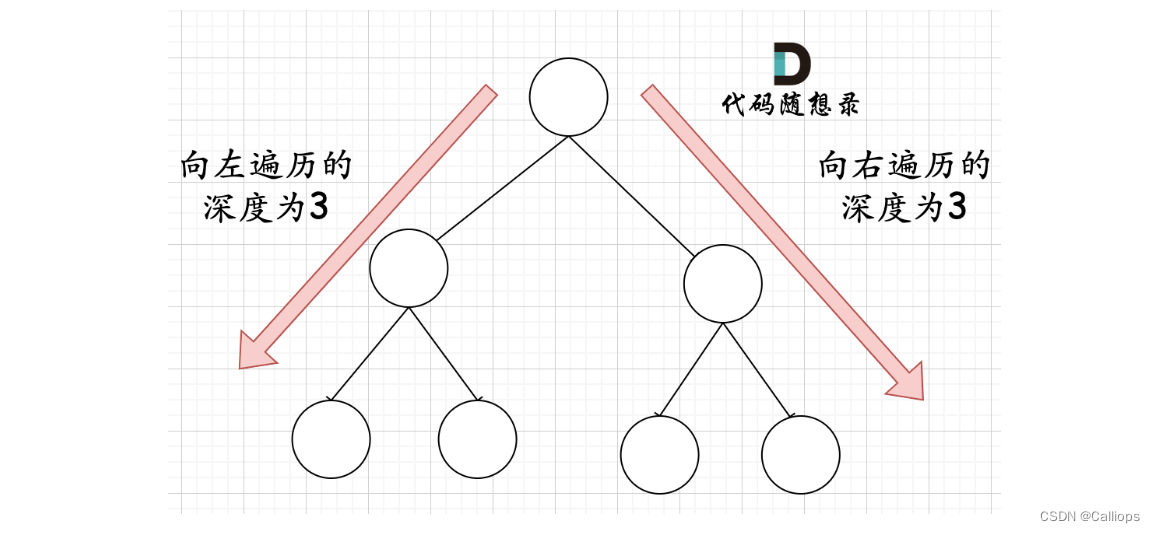
给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。 完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。 题解： 1）层序遍历 2）可以利用完全二叉树的性质来做，完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶
【经典算法】LeetCode 222. 完全二叉树的节点个数（Java/C/Python3实现含注释说明,Easy)
作者主页： 🔗进朱者赤的博客 精选专栏：🔗经典算法 作者简介：阿里非典型程序员一枚 ，记录在大厂的打怪升级之路。 一起学习Java、大数据、数据结构算法（公众号同名） ❤️觉得文章还不错的话欢迎大家点赞👍➕收藏⭐️➕评论，💬支持博主，记得点个大大的关注，持续更新🤞 ————————————————- 题目描述 给定一个完全二叉树，计算树的节点个数。完全二叉树的定义如下
(第29天)【leetcode题解】222、完全二叉树的节点个数 110、平衡二叉树 257、二叉树的所有路径
目录 222、完全二叉树的节点个数题目描述思路代码 110、平衡二叉树题目描述思路代码 257、二叉树的所有路径题目描述思路代码 总结 222、完全二叉树的节点个数 题目描述 给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。 完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的
代码随想录算法训练营Day17|404.左叶子之和 110.平衡二叉树 222.完全二叉树的节点个数
404.左叶子之和 1、这道题需要统计出所有左叶子结点的值的和，首先要明确左叶子节点指的左右孩子节点均为null的左节点。如上图就是4和6. 2.但是光凭叶子结点本身是无法判定左叶子的，因为左右孩子都是null，所以要从上一层节点往下判定。所以判断左叶子的条件语句应该是 root.left != null && root.left.leftnull && root.left.rightnull
【二叉树】Leetcode 222. 完全二叉树的节点个数【简单】
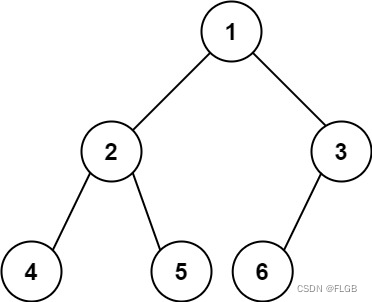
完全二叉树的节点个数 你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。 完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。 示例 1： 输入： root = [1,2,3,4,5,6] 输出： 6 解题思路 树的高度： 计
[力扣题解] 222. 完全二叉树的节点个数
题目：222. 完全二叉树的节点个数 思路 随便一种遍历方式都行 代码 Method 1 : Me class Solution {public:int countNodes(TreeNode* root) {if(root == NULL){return 0;}int result = 0;queue<TreeNode*> que;que.push(root);while(!que.
（二刷）代码随想录第16天|104.二叉树的最大深度 559.n叉树的最大深度● 111.二叉树的最小深度● 222.完全二叉树的节点个数
104.二叉树的最大深度 104. 二叉树的最大深度 - 力扣（LeetCode） 代码随想录 (programmercarl.com) 后序遍历： class Solution {public int maxDepth(TreeNode root) {// 如果当前节点为空，深度为0if (root == null) {return 0;}// 递归计算左子树的最大深度int left
day16二叉树part03 | 104.二叉树的最大深度 559.n叉树的最大深度 111.二叉树的最小深度 222.完全二叉树的节点个数
104.二叉树的最大深度 （优先掌握递归） 两种思路：1.使用递归，主要思想是递归遍历左右子树，然后左右子树高度的最大值加1即为当前节点的高度2.之前学习层次遍历的时候做过这题，直接在层次遍历的时候加上一个计数变量即可 思路1，递归法 class Solution {public:// 1.首先确定函数参数和返回值，要返回的是一个intint depth(TreeNode* root)
代码随想录算法训练营第16天 |● 104.二叉树的最大深度 559.n叉树的最大深度 ● 111.二叉树的最小深度 ● 222.完全二叉树的节点个数
文章目录 前言104.二叉树的最大深度思路知识点 方法一 递归法方法二 迭代法 559. n叉树的最大深度111.二叉树的最小深度思路方法一 后向遍历递归法方法二 迭代法 222.完全二叉树的节点个数思路方法一 当成普通二叉树来做方法二 利用完全二叉树的特性 总结 前言 所有的题目一刷都是优先掌握递归，迭代法没看，记不住。打十个做完之后再说吧 104和111没有看先序遍历的代
![【代码随想录】【算法训练营】【第16天】 [104]二叉树的最大深度 [111]二叉树的最小深度 [222]完全二叉树的节点个数](https://img-blog.csdnimg.cn/direct/b01e48a6f61c4f8ba135ea420a5d9ac9.png)
【代码随想录】【算法训练营】【第16天】 [104]二叉树的最大深度 [111]二叉树的最小深度 [222]完全二叉树的节点个数
前言 思路及算法思维，指路 代码随想录。 题目来自 LeetCode。 day 16，周四，再坚持一下吧~ 题目详情 [104] 二叉树的最大深度 题目描述 104 二叉树的最大深度 解题思路 前提：二叉树的最大深度，等价于二叉树的层数，等价于求最底层二叉树叶子结点的高度。 思路：求二叉树深度：前序遍历；求二叉树高度：后序遍历；求二叉树层数：层级遍历。 重点：二叉树节点的深度：指
Leetcode 222：完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。 递归遍历1 public static int countNodes(TreeNode root){return preorder(root);}//计算树的节点个数public static int preorder(TreeNode root){int count=0;if(root==null) return 0;int
【二叉树算法题记录】222. 完全二叉树的节点个数
题目描述 给你一棵 完全二叉树 的根节点root ，求出该树的节点个数。 完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。 题目分析 迭代法 简单暴力直接上层次遍历！（万能的层次遍历） /*** Definition for a bina
代码随想录算法训练营第19天 |104. 二叉树的最大深度 | 111. 二叉树的最小深度 | 222. 完全二叉树的节点个数
104. 二叉树的最大深度 题目链接 解：递归 /*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/int get_depth(struct TreeNode *node) {
算法练习第19天|222.完全二叉树的节点个数
222.完全二叉树的节点个数 222. 完全二叉树的节点个数 - 力扣（LeetCode）https://leetcode.cn/problems/count-complete-tree-nodes/description/ 题目描述： 给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。题目数据保证输入的树是 完全二叉树 完全二叉树 的定义如下：在完全二叉树中，除了最底层节点
HCIP-H12-222练习题
HCIP-H12-222练习题 习题 1 IP报文中用Tos字段进行Qos的标记，Tos字段中是使用前6bit来标记DSCP的。 A. 正确 B. 错误 答案: A 习题 2 传统的丢包策略采用尾部丢弃（Tail-Drop）的方法，这种丢弃方法会导致TCP全局同步现象。 A. 正确 B. 错误 答案: A 习题 3 下列选项中，属于Agile Controller的业务编排的亮点的是？ A. 基于
代码随想录训练营第三十五期|第天16|二叉树part03|104.二叉树的最大深度 ● 111.二叉树的最小深度● 222.完全二叉树的节点个数
104. 二叉树的最大深度 - 力扣（LeetCode） 递归，可以前序遍历，也可以后序遍历 前序遍历是backtracking 下面是后序遍历的代码： /*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;
【算法刷题day16】Leetcode:104.二叉树的最大深度 559.n叉树的最大深度 111.二叉树的最小深度 222.完全二叉树的节点个数
104.二叉树的最大深度 （优先掌握递归） 文档链接：[代码随想录] 题目链接：104.二叉树的最大深度 （优先掌握递归） 状态：ok 题目： 给定一个二叉树 root ，返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 注意： 1.暂时只看了递归的方法没有看迭代法 2.后序遍历会比前序遍历简单 class Solution {public:in
Day16:LeedCode 104.二叉树的最大深度 111.二叉树最小深度 222.完全二叉树的结点个数
104. 二叉树的最大深度 给定一个二叉树 root ，返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 思路:根结点最大深度=max(左子树最大深度,右子树最大深度)+1 终止条件,结点为null,该结点最大深度为0 class Solution {public int maxDepth(TreeNode root) {if(root==nu
KEBA HT401-222-8/0伺服控制器
KEBA HT401-222-8/0伺服控制器具有以下特点： 高精度和高响应速度：该控制器采用先进的控制算法和技术，能够实现高精度和高响应速度的伺服控制。多种控制模式：该控制器支持多种控制模式，如位置控制、速度控制、扭矩控制等，以满足不同应用场景的需求。易于编程和调试：该控制器提供丰富的编程接口和调试工具，方便用户进行二次开发和调试。可靠性高：该控制器采用高品质的材料和制造工艺，经过严格的质量控