【二叉树】Leetcode 222. 完全二叉树的节点个数【简单】

本文主要是介绍【二叉树】Leetcode 222. 完全二叉树的节点个数【简单】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

完全二叉树的节点个数

你一棵完全二叉树的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：
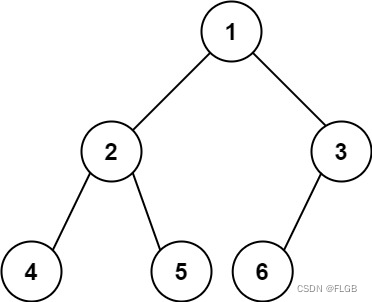
在这里插入图片描述
输入： root = [1,2,3,4,5,6]
输出： 6

解题思路

树的高度：

计算树的高度可以在 O(log n) 时间内完成，通过沿着左子树一直走到底。

完全二叉树的性质：

对于完全二叉树，如果左右子树的高度相同，那么左子树一定是满二叉树，可以直接计算其节点数；
如果左右子树的高度不同，那么右子树一定是满二叉树。

递归计算：

根据左右子树的高度关系，递归地计算左右子树的节点数，直到叶节点。

Java实现

public class CountNodes {public static class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) { val = x; }}/** 二叉树的节点数 */public int countNodes(TreeNode root) {if (root == null) {return 0;}int leftDepth = computeDepth(root.left);int rightDepth = computeDepth(root.right);if (leftDepth == rightDepth) {// 左子树是满二叉树return (1 << leftDepth) + countNodes(root.right);} else {// 右子树是满二叉树return (1 << rightDepth) + countNodes(root.left);}}/** 二叉树的深度 */private int computeDepth(TreeNode node) {int depth = 0;while (node != null) {node = node.left;depth++;}return depth;}public static void main(String[] args) {CountNodes countNodes = new CountNodes();// 构建示例完全二叉树TreeNode root = new TreeNode(1);root.left = new TreeNode(2);root.right = new TreeNode(3);root.left.left = new TreeNode(4);root.left.right = new TreeNode(5);root.right.left = new TreeNode(6);// 计算完全二叉树的节点个数int result = countNodes.countNodes(root);System.out.println("Number of nodes: " + result);  // 输出: 6}
}