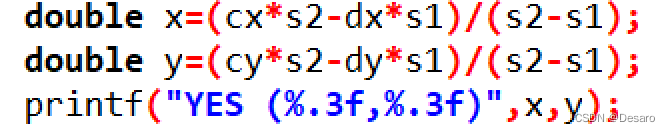精度的控制 第一种方法：int dblcmp(double x){if(fabs(x)<eps)return 0;return x>0?1:-1;}第二种方法：int dblcmp(double x){if(x>eps)return 1;else if(x<-eps)return -1;else return 0;} 叉积的求解 double det(double x1,do

两条线段有且仅有一个公共点，且这个点不是任何一条线段的端点时，称这两条线段是严格相交的。 也就是说线段不严格相交时可以将端点作为交点，但本文不讨论不严格相交，只讨论严格相交的情况（即使它们在算法实现上差别不大）。 在判断两条线段是否相交时，我们常用快速排斥实验跟跨立实验这两种方法，快速排斥实验能很快的排除掉线段不相交的情况，但并没法成为线段相交的充要条件，在快速排斥实验之后接上跨立实验就能完全

题目链接：zoj 1648 题意：给出n条边，问：如果有相交，输出burned！，没有输出ok！，注意下，这题还说了，相交于端点是不算交叉的。 参考链接：http://dev.gameres.com/Program/Abstract/Geometry.htm https://blog.csdn.net/freezhanacmore/article/details/7894751 http:

背景知识： 判断两线段是否相交：　　 我们分两步确定两条线段是否相交：　　 (1)快速排斥试验　　　　     设以线段 P1P2 为对角线的矩形为R，      设以线段 Q1Q2 为对角线的矩形为T，     如果R和T不相交，显然两线段不会相交。　　 (2)跨立试验 　　如果两线段相交，则两线段必然相互跨立对方。若P1P2跨立Q1Q2 ，则矢量 ( P1 - Q1 ) 和(

计算几何中,有 判断两个线段是否相交问题. 用到快速排斥实验和 跨立实验 快速排斥实验,是跨立实验的前提和基础. 假设有点 P1(x1,y1) P2(x2,y2)  Q1(x3,y3) Q2(x4,y4)  构成线段 P1P2  Q1Q2 问 P1P2与Q1Q2是否相交 快速排斥实验:    P1P2 对角线构成矩形R, Q1Q2对角线构成矩形T  若 R与T 相交着 通过快速排斥, 否则

线段相交有两种情形：一种是“规范相交”，另一种是“非规范相交”。规范相交是指两条线段恰有唯一一个不是端点的公共点。即如果一条线段的端点在另一条线段上则不视为相交。如果两条线段有部分重合，也不视为相交。而非规范相交则把以上两种情况都视为相交。如下图所示： 规范相交认为a，b两种情况都是不相交的，而非规范相交认为a，b两种情况都是相交的。 本题要求判断两条线段是否相交。如果是规范相交则输出